Mathématiques en biomédecine


La première irruption historique des mathématiques en médecine date de Daniel Bernoulli lorsqu’il présenta en 1760 à l’Académie royale des sciences un modèle mathématique construit avec une série d’équations différentielles de la diffusion de la variole permettant d’évaluer le bénéfice de la variolisation, procédé qui consistait à inoculer un sujet sain avec le pus d’un convalescent et qui anticipait donc la vaccination. Ce modèle mathématique démontra que le bénéfice de la variolisation l’emportait certainement sur le risque. Cette étude vraiment moderne aurait pu être réalisée aujourd’hui : il ne manquait rien, même pas les débats acharnés puisqu’il y eut à son sujet un conflit chaud avec d’Alembert.
À partir de la seconde moitié du XIXe siècle, la partie des mathématiques qui fut la plus concernée par la biomédecine est sans aucun doute la statistique et le calcul des probabilités. C’est qu’en effet la variabilité est une des caractéristiques les plus marquantes du vivant. D’ailleurs, s’il n’y avait pas de variabilité, il n’y aurait pas de vie : s’il y a une sélection naturelle, c’est bien parce qu’il y a une variabilité. Mais cette variabilité qui fait le charme de la vie est aussi source de grandes difficultés : deux malades ne sont jamais identiques, leurs signes diagnostiques sont différents, leur pronostic n’est pas le même. Chez l’un le traitement réussit, chez l’autre il ne réussit pas.
En 1930 le statisticien Fisher fondait les bases du test statistique de comparaison. La planification d’expériences scientifiques rigoureuses, reposant sur le tirage au sort pour décider qui est traité et qui ne l’est pas, puis la découverte de plans d’expériences puissants, éventuellement compliqués, s’appuyant quelquefois sur des résultats de géométrie non triviaux, suivirent.
En 1945, le premier essai thérapeutique randomisé était organisé sur l’homme. La méthodologie allait déferler sur la médecine dans l’ensemble du monde, générant de nombreux travaux méthodologiques. En France, Daniel Schwartz (37) allait être un des pionniers de cette nouvelle discipline et fonder une école. Cette méthodologie est en elle-même porteuse d’une véritable révolution dans le domaine médical (voir L’irruption de la médecine fondée sur la preuve scientifique, A.-J. Valleron, La Jaune et la Rouge, février 2001).
L’arbre de la statistique cachait néanmoins un peu la forêt des mathématiques. Depuis quelques années, on reparle de la forêt : tout d’abord l’usage des mathématiques en biomédecine est rendu plus facile grâce à la généralisation de l’informatisation dans les laboratoires, apportant des outils et des logiciels qui permettent de traiter des problèmes difficiles à traiter à la main.
Plus qu’autrefois, on a recours aux mathématiques dans ses rôles traditionnels : aider à décrire (comment mieux exprimer la forme de la courbe de croissance d’une culture cellulaire qu’en disant qu’elle est exponentielle, ou logarithmique, ou suit une fonction puissance…) ; ensuite, tirer le maximum des résultats expérimentaux lorsque les phénomènes sous-jacents peuvent s’exprimer mathématiquement d’une façon simple : dans cette catégorie, on trouve de nombreuses interprétations de données physiologiques, pharmacologiques où un système d’équation différentielle est facilement construit et où le but est d’estimer les paramètres, toujours en tenant compte des erreurs de mesures importantes en biologie et des variabilités inhérentes au phénomène biologique. Enfin, comme partout, les mathématiques en biomédecine sont un outil qui aide à formaliser les discours approximatifs, à simplifier, à comprendre.
Depuis quelques années, cependant, on assiste à un nouveau tournant où on ne considère plus les mathématiques en biomédecine comme une discipline importante, bien que relativement secondaire, mais où au contraire on commence à dire qu’elles sont la condition sine qua non du développement de la recherche en biologie et en médecine.
Le mathématicien Ian Stewart, auteur en particulier de livres sur le chaos qui sont devenus des best-sellers, et responsable de la rubrique des jeux mathématiques dans Scientific American a écrit il y a quelques années : » Je prédis – et je suis loin d’être le seul – que certains des progrès scientifiques les plus importants du vingt et unième siècle seront accomplis en biomathématiques. Ce siècle verra une explosion de nouveaux concepts mathématiques, de nouvelles formes de mathématiques engendrées par le besoin de comprendre l’organisation du monde vivant. Ces nouvelles idées interagiront de manière radicalement nouvelle avec les sciences de la vie et les sciences physiques. Elles fourniront – en cas de succès – une profonde compréhension de cet étrange phénomène que nous appelons » la vie « , un phénomène dont les étonnantes capacités résultent inévitablement de la richesse sous-jacente et de l’élégance mathématique de notre univers1. »
Comment vivre ce métier de » biomathématicien » ? Notre laboratoire comporte des chercheurs de différentes origines : grandes écoles (X, Mines, Centrale), facultés des sciences, facultés de médecine. Toutes ces personnes ont des façons d’exercer leur métier de chercheur qui varie (toujours la variabilité !). Nous avons choisi, pour traiter ce problème, de donner ci-dessous les témoignages personnels de deux chercheurs ayant eu la même formation (l’X), tous deux biomathématiciens, collaborant très facilement ensemble (malgré un certain nombre d’années d’écart) mais ayant des démarches différentes.
Témoignage de Alain-Jacques Valleron
À la sortie de l’École polytechnique, ma thèse concerna la modélisation du cycle cellulaire et de la cinétique des tumeurs. On venait en effet de mettre au point de nouvelles techniques expérimentales permettant de mesurer la durée de vie des cellules tumorales ou normales, la nature et la localisation d’événements internes au cycle cellulaire, et de mesurer à quel point cette durée était variable d’une cellule à l’autre au sein de la même tumeur, ou du même tissu normal. Ceci ouvrait l’espoir de concevoir des séquences de traitement par chimiothérapie ou par radiothérapie, idéalement espacées, tuant un maximum de cellules de la tumeur, et seulement un minimum de cellules saines en exploitant le mieux possible les différences de cinétique entre les tumeurs et les tissus sains. Les données expérimentales permettant de connaître ces cinétiques étaient ininterprétables » à la main » : il fallait modéliser la variabilité des événements d’une cellule à l’autre, en définissant des lois de probabilité convenables. Une fois estimée cette variabilité, ses conséquences nécessitaient aussi le recours à la modélisation mathématique.
Je me lançai avec entrain dans ce travail, mais réalisai rapidement qu’il était impossible de modéliser des données expérimentales sans connaître les techniques correspondantes utilisées au laboratoire, sans traquer les sources d’erreur, sans considérer les contraintes pratiques qui interdisaient de demander des données a priori très informatives mais nécessitant des jours et des nuits consécutives de plusieurs techniciens ! Vint même le moment où il devint évident que je devais moi-même faire quelques travaux expérimentaux qui me menèrent, non sans mal, à rechercher la rate à l’intérieur de la souris que j’avais préalablement » sacrifiée « , à compter et recompter des nodules qui étaient toujours en nombre différent, à ne plus me souvenir avec certitude si le groupe de souris de la cage 17 était bien le groupe irradié à 750 rads, etc.
À cette époque, choisir les Sciences de la vie à la sortie de l’École polytechnique paraissait extravagant. Cependant, en dehors de l’École, des mathématiciens commençaient à s’intéresser au couple mathématiques-biologie. C’était en particulier le cas de René Thom, avec sa théorie des catastrophes. Je fus invité à parler de ce que je faisais dans un séminaire de tels mathématiciens. Je commençais donc par raconter quel était le but ultime qui me faisait rêver (celui signalé ci-dessus : aider à mettre au point des traitements anticancéreux plus efficaces en faisant dire plus aux données expérimentales grâce à la modélisation).
(Source : Science, 23 novembre 2001.)
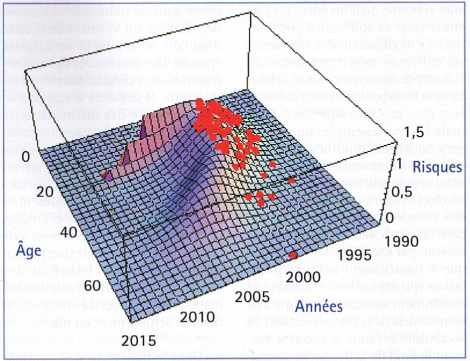
Des méthodes statistiques (estimations du maximum de vraisemblance sur données tronquées) et des techniques d’analyse numérique puissantes sont nécessaires.
La surface 3D représente le modèle d’épidémie obtenu où le pic est trouvé vers 2001–2002, et une bimodalité de la distribution des âges est prévue.
Mais je fus vite arrêté dans mon introduction par un auditeur mécontent : » Vous parlez de cellule, alors que vous avez omis d’en donner la définition. » Ce jour-là, à ce moment-là, je compris que j’étais passé dans un monde différent de celui des mathématiciens : je m’intéressais à un objet, les mathématiques n’étaient que mes serviteurs.
Le modélisateur en biologie est en effet un biologiste, non un mathématicien : son but est de faire avancer un domaine précis de la biologie. Si pour ce faire, une règle de trois est suffisante, tant mieux ! Quant au succès, il le trouve lorsque les biologistes et les médecins considèrent qu’ils sont face à un résultat original qu’ils n’auraient pu obtenir sans lui.
La première qualité du modélisateur est donc d’être capable d’acquérir la culture du domaine auquel il s’intéresse. Il doit aussi avoir une culture mathématique large, notamment en calcul des probabilités et en statistique, indispensables à la représentation et l’interprétation de la variabilité qui est omniprésente en biomédecine. Ce doit être au départ un excellent généraliste des mathématiques, et à l’arrivée un spécialiste du domaine auquel il s’intéresse. Au contraire, je n’ai que méfiance pour le spécialiste du calcul différentiel qui ne s’intéresse qu’à ceux des problèmes biologiques qui peuvent se mettre sous la forme d’un système d’équations différentielles.
La suite de mon expérience professionnelle en modélisation concerne depuis longtemps la modélisation en épidémiologie, avec l’arrivée des maladies émergentes (sida : 1981, hépatite C : 1990 ; nouveau variant de Creutzfeldt Jakob : 1996), on s’est trouvé devant une situation nouvelle : seulement quelques cas de malades sont connus au début (par exemple, au total c’est environ » seulement » 120 cas du nouveau variant de Creutzfeldt Jakob qui ont été identifiés pour l’instant). On veut pourtant le plus vite possible pouvoir donner des informations sur les caractéristiques de la maladie, et les risques qu’elle représente dans l’avenir. Prenons l’exemple de la durée d’incubation : comment faire pour estimer ce que sera sa durée moyenne dans une maladie qu’on ne connaît que depuis quelques années, alors qu’on a le soupçon, basé sur la connaissance de maladies semblables, qu’elle peut être très longue ?
La seule façon de répondre est d’utiliser la modélisation : la force de la méthode est qu’elle oblige à spécifier toutes les hypothèses et que chacun, dans le monde entier, peut non seulement répliquer les résultats mais critiquer telle ou telle hypothèse, la modifier, et voir quelle en est la conséquence. La modélisation est aussi l’outil indispensable de l’épidémiologie prévisionnelle : combien de cas de sida, ou de cancers du foie causés par l’hépatite C, ou de nouveau variant de Creutzfeldt Jakob peut-on attendre dans les années qui viennent en fonction de telle ou telle hypothèse ?
Combien de cas de cancer l’exposition à une très faible dose de radiations peut-elle entraîner ? Toutes questions qui ne trouvent leur réponse que dans la modélisation. Là aussi, la polyvalence technique, la capacité d’écoute des autres disciplines est une qualité indispensable à l’exercice du métier. La mesure devant l’incrédulité de certains face à la modélisation et la crédulité des autres face à la magie des mots mathématiques est une autre qualité importante dans des domaines où les résultats peuvent être très sensibles dans la société…
Ne pas croire que le modélisateur ayant les caractéristiques que je trouve souhaitables est attendu et fêté comme le messie par tous les biologistes. Beaucoup lui exprimeront la défiance qu’ils ont pour ses » modèles » qui sont » trop distincts de la réalité » ! Ceci, de mon point de vue, est injuste. Le modèle est » un objet substitué à la réalité dans un but déterminé « . Il n’est pas substituable à la réalité dans n’importe quel but, car il faudrait qu’il lui soit identique (tel le héros de La Mémoire de Borgès, dont la mémoire était si bonne qu’il lui fallait un jour entier pour se souvenir d’une journée).
Le modélisateur doit convaincre ses collègues expérimentateurs de l’identité de son approche avec la leur : lorsque les expérimentateurs construisent des » modèles animaux » d’une maladie (par exemple, une souris génétiquement modifiée pour être obèse), ils substituent à la réalité (l’obésité d’origine génétique chez l’homme) un objet (la souris modifiée) qui pourra être substitué à la réalité (l’homme) dans un but déterminé (tester un traitement, par exemple). Il est essentiel que le modélisateur et l’expérimentateur qui travaillent ensemble se construisent une connivence qui aille bien au-delà de la compréhension du vocabulaire de l’autre, et concerne vraiment le fond de la démarche scientifique.
C’est d’ailleurs ainsi qu’il sera possible par exemple que le modélisateur participe à l’invention de nouveaux schémas expérimentaux, ce qui est de mon point de vue toujours à rechercher, il doit en effet y avoir un aller et retour permanent entre la modélisation et l’expérimentation : la modélisation permet d’abord de tirer le maximum d’information des données expérimentales existantes, puis elle doit permettre d’imaginer quelles sont les prochaines expériences, ou observations, qui seraient les mieux à même de trancher entre deux hypothèses, ou d’estimer un paramètre important.
Témoignage de Khachayar Pakdaman
The unreasonable effectiveness of mathematics in molecular biology. Ce titre intriguant et provocateur2, qui débute un récent article (d’Arthur M. Lesk) dans le Mathematical Intelligencer (vol. 222 2000), l’est d’autant plus que son auteur a hésité jusqu’à la dernière minute entre cet intitulé et The unreasonable in-effectiveness…, comme le révèle un numéro ultérieur du même journal (vol. 23 (4) 2001).
Deux titres opposés, un choix final politiquement correct : peut-on être plus ambivalent envers l’emploi des mathématiques en biologie ? Loin d’être propre à cet auteur, ou à la biologie moléculaire, cette attitude existe dans de nombreux domaines des sciences du vivant. Elle illustre d’un côté le sentiment de surprise éprouvé face aux succès des mathématiques dans certains domaines biomédicaux, et de l’autre le scepticisme envers l’utilité des mathématiques dans bon nombre de disciplines traitant du vivant.
Dans la suite de ce témoignage, je vais présenter un exemple considéré » classique » de succès des mathématiques dans mon propre domaine de recherche. Ensuite, je discuterai de ce qui à mon avis constitue la nouvelle démarche biomathématique qui bénéficie des meilleures interactions entre mathématiques et sciences du vivant qui se mettent actuellement en place.
Dans le traitement de l’information par le système nerveux, tout passe par le codage neuronal. En résumé, pour communiquer, une cellule nerveuse, ou neurone, envoie à un autre neurone une décharge électrique qui dure quelques millisecondes et met en jeu une centaine de millivolts, avant de retourner au repos. La forme et la durée d’une décharge varient peu, et de fait, la transmission d’information nécessite une série de ces décharges, comme dans le code Morse.
Mais quel lien unit l’information que reçoit le neurone et la série d’impulsions qu’elle déclenche ? En étudiant les flots du tore (une classe d’équations différentielles), il est douteux que Henri Poincaré ait pensé participer à la résolution de cette question. Cependant, c’est précisément grâce à ses résultats, et à ceux des mathématiciens qui ont poursuivi ses travaux, que l’on peut élaborer des hypothèses concernant les principes de ce codage, et que des applications dans le domaine biomédical sont aujourd’hui possibles.
Dès les années vingt, on savait que la fréquence de décharge du neurone sensoriel croît avec l’intensité de la stimulation, faisant du codage en fréquence le candidat probable du codage neuronal (E. D. Adrien, The mechanism of nervous action, University of Pennsylvania Press, 1932). Cependant, en 1964, un groupe mixte de la Rand Corporation et d’UCLA remettait en cause ce point de vue (Perkel et al., Science 145 : 61–63, 1964). En effet, si le codage était uniquement fréquentiel, il était nécessaire que la fréquence moyenne de décharge d’un neurone reflète de manière univoque l’information reçue.
Or, ce n’était pas le cas dans leurs expériences : pour des stimulations périodiques, la fréquence moyenne de décharge du neurone ne variait pas de manière monotone avec celle de l’entrée, mais très nettement en dents de scie. La démarche suivie par les auteurs pour exploiter ces observations a alors été remarquable : plutôt que de mettre en place des expériences pour rechercher les bases moléculaires ou chimiques expliquant le comportement complexe et inattendu des neurones, ce qui aurait été attendu dans leur discipline, ils adoptèrent une approche radicalement différente, en formulant un modèle mathématique élémentaire, capable toutefois de reproduire les comportements observés. Celui-ci revenait finalement à étudier la dynamique d’une application allant du cercle dans lui-même : voici le tore de Poincaré.
L’étude de ce modèle mathématique a révélé que la réponse en dents de scie correspondait à l’organisation particulière des solutions périodiques associée à l’application du cercle. Les mathématiciens avaient démontré que la clé de cette organisation résidait dans les propriétés » géométriques » de ces applications. Or ces mêmes propriétés apparaissaient dans de nombreux processus, aussi divers que la convection d’un fluide, et certaines réactions chimiques. Ainsi, la réponse en dents de scie du neurone s’observait aussi dans des systèmes biologiques, physiques et chimiques régis par des mécanismes totalement différents (voir par exemple L. Glass, MC Mackey, From clocks to chaos, Princeton University Press, 1988 ; P. Berger et al. L’ordre dans le chaos, Hermann, 1988).
La conception d’un modèle mathématique avait donc permis de mieux comprendre les principes régissant le codage d’une stimulation périodique par un neurone. Elle permettait également de penser qu’il existait des systèmes biologiques, physiques et chimiques organisés selon des principes identiques. Par le biais de la modélisation mathématique, un langage commun, propice à la collaboration, était né entre les chercheurs de ces différentes disciplines.
Aujourd’hui, près de quarante ans après l’expérience de codage neuronal décrite plus haut, l’étude des propriétés de modèles mathématiques, et plus précisément des systèmes dynamiques, est partie intégrante de la culture d’analyse et de modélisation en sciences de la vie.
Il existe de nombreux séminaires et congrès où biologistes, chimistes, mathématiciens, médecins et physiciens se retrouvent et de nombreux projets interdisplinaires sur lesquels ils travaillent ensemble. En 2001, ces échanges interdisciplinaires ont trouvé une concrétisation remarquable dans le domaine biomédical, où l’utilisation de méthodes développées dans l’analyse de dynamiques non-linéaires ont permis d’anticiper l’occurrence de crises d’épilepsie à partir d’enregistrements électro-encéphalographiques (Le van Quyen et al. Lancet, 357 : 183–188, 2001).
L’exemple du lien qui s’est progressivement tissé entre les neurosciences et les méthodes géométriques des systèmes dynamiques illustre parfaitement le sens que l’on peut donner au titre du Mathematical Intelligencer cité plus haut : il arrive que la modélisation mathématique d’un processus biologique puisse rendre compte non seulement d’un vaste ensemble de données expérimentales, et qu’elle se révèle même assez riche pour initier de nouvelles expériences ou applications qui entraîneront des changements profonds dans les sciences de la vie.
Ce même exemple a longtemps illustré la démarche biomathématique : l’application astucieuse de théorèmes mathématiques, déjà connus, à l’étude de systèmes biologiques. La surprise devant le succès de cette méthode était d’autant plus grande que la motivation initiale du mathématicien (la mécanique céleste pour Poincaré) était éloignée du domaine d’application biologique (le codage neuronal).
Mais cette surprise reflétait aussi la faiblesse de la méthode, car le lien tissé entre théorie mathématique et problème biologique semblait dû au hasard, et renforçait alors le scepticisme quant à l’apport des mathématiques dans d’autres problèmes biologiques.
Aujourd’hui, la démarche biomathématique ne veut plus être fortuite : à l’instar de la physique, qui a nourri de multiples développements mathématiques, la biologie devient une force motrice pour les mathématiques. Les problèmes biologiques donnent lieu à des recherches mathématiques originales, et, en retour, ces recherches permettent des applications biomédicales innovantes. C’est cette nouvelle alliance entre les deux disciplines, qui en transgressant les barrières » culturelles » qui rendaient le dialogue difficile, est source de l’optimisme d’Ian Stewart quant à l’avenir des biomathématiques.
En conclusion
Francis Crick, qui a proposé, avec James Watson, la structure en double hélice de l’ADN, se rappelant les liens qui se sont établis entre la biochimie et la génétique dans les années cinquante, fait la remarque suivante à ceux qui veulent jeter des ponts entre disciplines distinctes3 :
» Je ne suis pas certain que les arguments logiques, aussi solides soient-ils, servent à grand-chose. Ils peuvent peut-être contribuer à une prise de conscience, mais ne permettent pas, en général, d’aller plus loin. Il eût été difficile, par exemple, de convaincre les généticiens d’apprendre la chimie des protéines avec pour seul argument que quelques types futés croyaient que c’était la direction que devait suivre la génétique […] Pour que les gens saisissent véritablement le lien qui existe entre deux domaines, il faut un résultat nouveau et spectaculaire qui éclaire le lien de manière frappante. Un bon exemple vaut mieux que des tonnes d’arguments théoriques. Une fois qu’un tel exemple a été trouvé, il se forme rapidement un embouteillage sur le pont qui relie les deux disciplines, tant il y a de chercheurs qui souhaitent emprunter la nouvelle voie. »
Le constat de Crick s’applique aussi aux biomathématiques. Des résultats nouveaux et spectaculaires, dont seulement quelques-uns ont été mentionnés ci-dessus, ont aussi contribué à attirer de nombreux chercheurs sur le pont qui relie biomédecine et mathématiques (créant même des embouteillages par endroit, bien que, si l’on en croit Ian Stewart, le pire reste encore à venir !). De ce fait, on y trouve aussi bien des biologistes qui utilisent tout simplement les outils mathématiques, que les mathématiciens qui démontrent des » bio-théorèmes « 4, c’est-à-dire des théorèmes motivés et guidés de près par une problématique biologique.
La formation
Quelle que soit l’approche individuelle qui est choisie pour faire des biomathématiques, la recommandation principale qu’on peut faire aux candidats est d’avoir une culture extrêmement large en mathématiques et, bien sûr, une passion pour l’objet biologique.
De ce point de vue, il faut bien reconnaître que la formation » généraliste » de qualité des grandes écoles est un atout pour ce métier.
____________________________________________
1. Extrait traduit de Ian Stewart, Life’s Other Secret, Allen Lane the Penguin Press, 1998.
2. Inspiré de celui d’un texte d’Eugene Wigner, prix Nobel de physique, » The unreasonable effectiveness of mathematics in natural sciences » in Communications in Pure and Applies Mathematics, vol. 13, n° 1 (février 1960). New York : John Wiley & Sons, Inc.
3. Francis Crick, Une vie à découvrir, Éditions Odile Jacob, 1989.
4. Clin d’œil à la mode actuelle de fabriquer des mots à préfixe » bio » !