Risk Management et transparence des risques financiers


Le manque de transparence des risques, bien plus que les problèmes de comptabilités, est le véritable fondement de la crise de confiance majeure que les marchés financiers ont connue en 2002.
La comptabilité même sincère ne peut en soi rendre compte des risques pesant sur la valeur future d’une entreprise. Les faillites WorldCom et Enron ne résultent pas uniquement de la fraude comptable, mais bien de la matérialisation de risques depuis longtemps quantifiables, sur lesquels les marchés ont été aveugles, faute de transparence. Restaurer la confiance des investisseurs impose donc de généraliser la transparence de risques, au travers d’une extension du risk management à la gestion d’actifs.
Cette extension se heurte toutefois aux coûts très élevés de la collecte et de la consolidation des risques le long des chaînes de valeur ajoutée. Elle ne devient en pratique possible qu’avec le développement d’une représentation additive et universelle des risques.
La nécessaire extension du domaine du risk management
L’adéquation des fonds propres
La créativité des marchés financiers en termes d’instruments dérivés, qui s’est accompagnée de quelques sinistres retentissants, a conduit la communauté financière à se doter au cours des années 1990 de nouvelles règles de détermination des fonds propres minimaux requis pour mener une activité bancaire (Basle I – Capital adequacy). En effet, l’approche traditionnelle par ratios de bilan devient totalement inappropriée quand se multiplient à l’infini les engagements » hors bilan » et les effets de levier implicites que l’on trouve dans tous les instruments financiers.
On est donc revenu à une définition naturelle des fonds propres requis : ils doivent permettre de couvrir les pertes potentielles résultant des engagements financiers nets. C’est bien là effectivement la fonction des fonds propres que d’être capable d’absorber les pertes futures. Cette définition logique nécessite une quantification de la notion de pertes potentielles : c’est la Value at risk.
Les principes déterminant sa mesure reposent sur une méthodologie rigoureuse et un ensemble de pratiques éprouvées, mis en œuvre par une profession reconnue dans les banques : les risk managers.
La budgétisation des risques
Il est essentiel pour l’investisseur d’avoir un profil de risque de son actif qui soit cohérent avec celui de son passif. Ainsi, jouer l’argent des prochaines vacances en valeurs du nouveau marché n’est pas recommandé. Plus sérieusement, avoir pour une grande compagnie d’assurances beaucoup d’actions des compagnies qu’elle assure peut être un moyen très sûr de maximiser son risque en minimisant ses performances.
Les investisseurs n’ont certes pas attendu le risk management pour tenter d’imposer une contrainte de risque, en fixant des obligations de moyens aux gestionnaires d’actifs, telles que les limites des traders, les mandats des gérants, la corporate governance pour les dirigeants d’entreprise, etc.
Le problème est que ces obligations de moyens n’offrent pas de garantie réelle en termes d’exposition au risque. Imaginons, par exemple, un investisseur qui ne veut pas de risque pays émergents, c’est-à-dire qui ne veut pas voir la valeur de son portefeuille s’effondrer quand les indices » pays émergents » plongent. Il confie au gérant un mandat lui demandant de n’investir que dans les valeurs » Stoxx 50 « .
Ceci ne l’empêchera pas d’avoir un portefeuille sensible de manière significative aux dits pays émergents, parce que le gérant aura investi dans des actions de banques européennes ayant un portefeuille significatif de prêts à ces pays.Le risk management permet au contraire d’objectiver le profil de risque d’un portefeuille, et donc de définir de manière claire les contraintes de risque, telles que la volatilité ex ante (c’est-à-dire future prédite) du portefeuille, sa Value at risk, sa Tracking error ex ante (l’écart type des différences de rendement avec un indice de référence) et ses sensibilités par rapport à des indices thématiques (pays, secteurs, styles, etc.).
L’optimisation rendement/risque
La définition d’un » budget de risque » a enfin pour vertu d’objectiver la notion de performance optimale.
Les déconvenues boursières de beaucoup d’investisseurs démontrent s’il en est besoin qu’une allocation de capitaux fondée sur la base des seules performances historiques (ex post) conduit souvent à un désastre. La raison en est que pour maximiser son espérance de bonus, un trader, un gérant ou un dirigeant d’entreprise (qui n’a à perdre que son emploi) doit minimiser la probabilité de pertes pour l’investisseur, c’est-à-dire en réalité maximiser le risque.
On peut ainsi en tant que gérant gagner très bien sa vie tout en offrant en réalité à ses clients une espérance de gain nul, avec des bénéfices réguliers et des pertes hautement improbables, mais monstrueuses.
Techniquement parlant, il s’agit d’une martingale : on cache les pertes dans les queues de distribution.
Dès lors que des contraintes de risque ex ante claires ont été spécifiées, la relation investisseur/gérant devient structurellement beaucoup plus saine : le gérant a pour mandat de maximiser le rendement sous contrainte de risque.
Le risk management offre en outre au gérant les techniques permettant de rechercher la » frontière efficiente » de son portefeuille : le principe fondamental de rechercher la diversification optimale, celle où la contribution marginale de chaque actif au risque doit être proportionnelle à la contribution marginale de ce même actif au rendement.
Des coûts de consolidation trop élevés
|
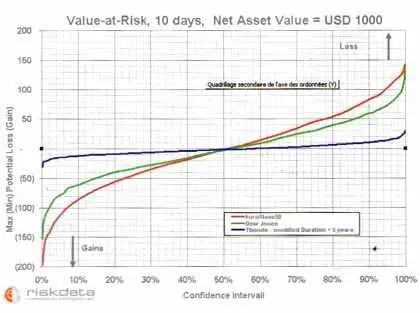
1 – Value at risk
La Value at risk n’a rien d’ésotérique : il s’agit du montant maximum de la perte possible, pour un intervalle de confiance et un horizon de temps donnés. Ainsi, les exemples cidessous se lisent comme suit : si on achète pour 1 000 dollars d’un portefeuille répliquant l’Euro Stoxx 50, on a 95 % de chances de perdre moins de 83 dollars dans les deux semaines à venir, et on a 5 % de chances de gagner au moins 98 dollars (les gains sont présentés comme négatifs, puisqu’on parle de valeur en risque).
Attention ! N’en déduisez pas qu’il faut acheter : l’espérance moyenne de gain est par construction proche de zéro (hypothèse dite » risque neutre »). |
|
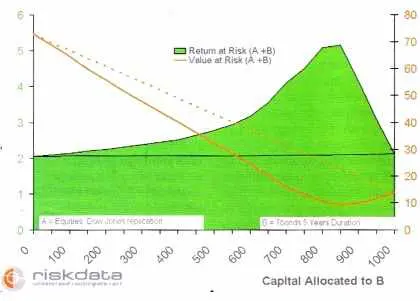
2 – Maximiser le Return at risk grâce à la diversification
entre une poche actions (A, qui réplique le Dow Jones) et une poche obligations (B, Tbonds US avec une durée de cinq ans), en fonction du capital alloué à B (sur un montant total de 1 000 euros). La courbe orange est le risque (Value at risk) fonction du montant alloué aux obligations. En orange pointillé, le risque du portefeuille si le risque se comportait de manière additive. La surface verte représente le Return at risk, c’est-à-dire le ratio entre le gain attendu et le risque : le vert pointillé correspond au Return at risk qui résulterait d’un indicateur de risque additif.
|
 |
Si les objectifs sont clairs et la théorie scientifique bien établie (cf. encadré), leur mise en œuvre soulève des difficultés pratiques très sérieuses.
En premier lieu, l’objectif pratique de l’investisseur averti est de pouvoir collecter pour chaque actif/fonds/ gérant les informations de risque, à une fréquence pertinente par rapport à l’horizon de gestion de l’investisseur et du gérant (par exemple, pour un day trader, collecter une fois par mois des informations de risque n’a pas beaucoup de sens).
En second lieu, il doit pouvoir consolider les informations de risque ainsi collectées, de manière non seulement à mesurer son exposition globale en termes de risque, mais également à gérer son allocation entre fonds pour optimiser son ratio rendement/ risque.
Cette exigence de collecte et de consolidation existe à l’intérieur d’une entreprise. Elle est également essentielle entre tous les niveaux de consolidation, depuis le gérant ou le trader en passant jusqu’à l’investisseur institutionnel, qui doit contrôler l’adéquation entre le risque de son actif et le risque de son passif.
Le problème paraît en apparence aussi simple que de calculer la valeur d’un portefeuille, pour lequel il suffit de collecter les valeurs des actifs et des fonds qui le composent, puis de les additionner pour calculer la valeur de l’actif consolidé.La réalité est beaucoup plus complexe, parce que les indicateurs de risque ne se comportent pas comme les prix.
Pour reprendre l’exemple illustré dans l’encadré 2, si on a dans la poche A 150 euros en actions (Value at risk = 10,2 euros) et dans la poche B 850 euros en obligations (Value at risk = 9 euros), le portefeuille A + B aura lui une Value at risk de 8,5 euros, c’est-à-dire non seulement très inférieure à la somme des risques de A et de B, mais même inférieure au risque du moins volatil des deux portefeuilles : en d’autres termes, il est moins risqué d’avoir un portefeuille fait de 150 euros d’actions et de 850 euros d’obligations que d’avoir un portefeuille de 1 000 euros d’obligations !
On pourrait imaginer toutefois que la connaissance du risque de A et celle de B permettent d’en déduire le risque de A + B. Il n’en est malheureusement rien, car un troisième paramètre se glisse dans l’affaire, la corrélation, qui ne dépend ni du risque de A ni du risque de B.
Pour reprendre l’exemple ci-dessus, si A était anticorrélé à 100 % avec B, le risque consolidé serait nul, s’il était corrélé à 100 %, le risque serait la somme des deux risques, si la corrélation est nulle, le risque est la racine carrée de la somme des carrés.
Le phénomène étonnant observé sur ce portefeuille vient du fait que les actions et les obligations sont anticorrélées à 45 %.
Les coûts informatiques associés aux modèles de Value at risk
De ce fait, la seule façon de consolider le risque est de revenir à la composition élémentaire de chaque sous-jacent, et connaître toutes les corrélations croisées entre eux. Si ainsi on investit 1 000 euros dans deux OPVCM, il faut connaître le détail des positions de chaque OPCVM et les corrélations croisées entre tous les composants élémentaires pour pouvoir connaître le risque global.
Ainsi, les systèmes de risk management développés par les grandes banques imposent de centraliser la description de tous les portefeuilles et des instruments dérivés, pour être en mesure de produire un chiffre pertinent pour le risque consolidé de la banque.
En pratique, si un tel projet peut aboutir – au prix d’un budget considérable – si le client est unique (par exemple la direction des risques d’une grande banque avec des besoins prévisibles et stables), il n’aura pas la flexibilité permettant de répondre aux attentes de clients multiples en termes de réactivité (les salles de marché ont, par exemple, besoin de temps réel), de nature de risques à suivre (dépendant du style de gestion), de type de tableaux de bord (pour un asset manager, en pratique autant que d’investisseurs institutionnels), etc.
L’impossibilité d’intégrer la diversification multimarchés et les produits dérivés dans les modèles factoriels
Les fonds de pension américains ont, dès les années 1980, cherché à promouvoir un cadre leur permettant de consolider le risque de leurs actifs, confiés à une multitude de gérants. Il était bien sûr exclu d’y parvenir par la création d’une base de données centralisée des positions.
Les fondements scientifiques de la gestion des risques
La statistique et le stress test
Le calcul du risque des institutions financières repose avant tout sur une étude statistique des données de marché : cours des actions cotées, taux d’intérêt et de change, obligations, commodités, produits dérivés (swaps, futures, options…). Une grande variété de modèles statistiques, tant au niveau de chaque actif pris individuellement que de l’ensemble des actifs contenus dans un portefeuille, ont été étudiés et développés. Ces modèles vont de la simple analyse en variance-covariance à des modèles paramétriques sophistiqués (lois de Pareto-Lévy, modèles GARCH, etc.), en passant par une analyse pragmatique des comportements globaux des marchés durant les différentes crises passées.
Le principe d’évaluation du risque consiste à estimer une distribution de probabilité de la valeur d’un portefeuille, potentiellement complexe, à un horizon de temps déterminé, ce afin d’optimiser les décisions concernant la gestion du portefeuille.
L’approche » historique » consiste à transposer dans la configuration de marché du jour les mouvements observés dans un passé plus ou moins récent. Notons que cette » transposition » présente des difficultés dans le cas des produits dérivés, à cause de leur comportement non linéaire par rapport aux autres actifs. Celles-ci sont surmontées grâce à l’introduction de » variables de marché » abstraites et faciles à transposer, par exemple, la » volatilité implicite » des options, issue du modèle de Black & Scholes.
L’analyse statistique reste incomplète si on ne lui associe pas une série de stress tests consistant à étudier de manière spécifique le comportement du portefeuille sous l’effet de certaines crises passées ou imaginées. En effet, ces crises correspondent à des événements rares, donc souvent hors statistiques, mais qu’il serait dangereux d’ignorer, l’impact effectif de ces événements étant plus important que leur probabilité d’occurrence.
Simulations de Monte-Carlo
D’un point de vue pratique, la présence, dans les portefeuilles, de nombreux produits dérivés et d’engagements » hors bilan » fait sortir leur évaluation du cadre linéaire par rapport aux variables dont on estime la distribution de probabilité. Les techniques traditionnelles de calcul du risque, reposant sur une simple analyse en variance-covariance des prix des actifs, se montrent insuffisantes — et pas seulement pour gagner quelques décimales de précision, mais bien pour l’ordre de grandeur de la Value at risk. Ces techniques avaient été développées à l’époque pour des raisons de maîtrise des temps de calcul aujourd’hui obsolètes. La méthode de simulations pseudo-aléatoires dite de » Monte-Carlo » s’avère in fine la plus performante pour simuler toute la complexité des actifs financiers échangés. En outre, elle apporte une souplesse incomparable dès qu’apparaît un nouveau type de produits, se marie aisément aux stress tests et peut, sans difficulté, intégrer toutes les subtilités des comportements joints des actifs observés sur les séries historiques.
La preuve
L’évaluation d’un modèle de calcul de risque, voire, plus précisément, d’une procédure complète de sa mesure, se fait par le back-testing. Lorsque, comme aux États-Unis, la météo annonce la pluie avec une probabilité de 60 %, on peut vérifier après coup si, sur l’ensemble des jours où la pluie a été prévue avec une telle probabilité, elle a eu lieu dans cette proportion. Il en va de même pour les risques financiers : le back-testing permet de comparer la distribution de probabilité des retours sur investissements effectivement observés pendant une période donnée avec la série de distributions théoriques fournies par le modèle pendant cette même période. Cette méthode permet de donner une assise solide aux différentes approches quantitatives testées, ainsi que de les comparer, à l’instar des expériences in vitro, et à l’inverse des modèles macroéconomiques, nécessairement in vivo.
Limites de validité
Il va de soi que l’évaluation du risque, comme décrite ci-dessus, n’a de sens que si l’évolution du marché dans l’avenir rentre dans le cadre de ce qui a été observé, même rarement, dans le passé. La statistique des marchés étant tout sauf stationnaire — qui peut prétendre aujourd’hui que la volatilité est une variable fixe, comme cela est stipulé dans l’article original de Black & Scholes ? — les deux propriétés fondamentales d’un » bon » modèle de risque sont la réactivité et la stabilité. En d’autres termes, le modèle se doit d’être suffisamment » lissant » pour que ses paramètres ne sautent pas chaque jour, mais assez souple pour réagir rapidement en cas de changement de régime. Chaque modèle, aussi précis soit-il, a de fortes chances d’être, un jour ou l’autre, mis en défaut par le comportement inattendu des marchés. Celui-ci sera trop conservateur et surestimera le risque pendant de longues périodes, ce qui peut entraîner en pratique des réductions importantes de performance cumulées. Celui-là est au contraire précis la plupart du temps, mais manque de prévoir la crise majeure, précisément ce que l’on attend de lui. D’une manière générale, l’optimisation des paramètres d’un modèle, afin que celui-ci remplisse les deux exigences de stabilité et de réactivité, est un art qui demande une certaine expérience, en même temps que l’accès à des données statistiques fiables. C’est pourquoi les modèles les plus performants restent l’apanage des grandes institutions financières ou de quelques entreprises spécialisées dans ce domaine.
Enjeux
Dans toute entreprise, c’est un lieu commun de dire que la gestion des risques n’est pas un gadget et fait partie du processus de décision au plus haut niveau. Dans la finance en particulier, monde » chiffres » s’il en est, cette tâche a la possibilité de se reposer sur des études quantitatives précises. Comme toujours, l’enjeu n’est pas de minimiser, voire d’éliminer totalement (fantasme !) le risque, mais de le maîtriser pour mieux en profiter. Les fonds de gestion alternative (hedge funds) connaissent bien cette problématique, puisque, en bons spéculateurs, leur but, dans la sélection de leurs martingales, est que leur chiffre de risque soit le plus proche possible de la performance espérée, ce qui signifie qu’ils n’en ont pas laissé inutilement de côté. D’une manière peut-être plus sage, mais au fond pas si différente, les gestionnaires de fonds traditionnels ont le même but lorsque, suivant les bons conseils de MM. Markovitz et Sharpe, ils cherchent à maximiser le rapport entre rendement et risque, ou encore à maximiser le rendement pour un chiffre de risque inférieur à une limite donnée. Là encore, l’introduction massive de produits dérivés dans les portefeuilles et la diminution du coût du calcul ont rendu incontournables les simulations de Monte-Carlo à des fins d’optimisation.
Cette demande a contribué à l’essor, côté asset management, des modèles factoriels de risque, qui ont le grand mérite d’être additifs et donc d’apporter une réponse simple à la demande de consolidation. Le modèle le plus simple est celui du » Bêta « , qui est la sensibilité d’un actif par rapport à un indice de marché. Par exemple, une action qui a un Bêta de 0,8 par rapport au CAC 40 veut dire qu’en moyenne, quand le CAC augmente de 10 %, l’action augmente de 8 %.
Si elle a connu de grands raffinements au cours des années 1990 (essentiellement, la multiplication du nombre de facteurs), cette famille de modèles arrive aujourd’hui en fin de vie pour trois raisons fondamentales.
Tout d’abord, ces modèles reposent sur une modélisation ad hoc des marchés, loin des canons scientifiques du risk management, et ont de ce fait une qualité prédictive médiocre. Les risques sont en général assez systématiquement sous-estimés. Or, les gestionnaires d’actifs sont à juste titre de plus en plus exigeants quant à la qualité prédictive de leurs indicateurs de risque – car ils sont soumis de facto à une obligation de résultat.
Ensuite, elle est inapte à donner une description des risques multimarchés. On peut développer un modèle factoriel pertinent pour le marché actions, un autre pour les taux. En revanche, il est impossible d’offrir un cadre de cette nature satisfaisant et commun aux deux. De ce fait, ces modèles ne permettent pas de consolider le risque sur les portefeuilles diversifiés, ceux-là mêmes qui répondent le mieux à la demande de diversification des investisseurs.
Elle ne permet pas de traiter des actifs non linéaires, tels que les produits de crédit, les dérivés, les asset-backed securities, etc.
Le monopole de fait très contraignant qu’induisent les approches de type ASP
La troisième voie proposée aujourd’hui est celle de l’ASP (Application service provider). Elle consiste à partager entre utilisateurs un système de calcul de risque. Partageant le même système la communauté des adhérents de l’ASP peut de ce fait agréger toutes les informations de risque. La contrepartie est l’obligation pour les utilisateurs de transférer la totalité de la composition de leurs portefeuilles à cet ASP, ce qui représente non seulement un coût d’intégration élevé et introduit une forte rigidité dans le format des analyses de risque, mais induit des risques significatifs en termes de confidentialité de l’information.
La logique de ce système, pour fonctionner, est que le maillon ultime de consolidation du risque impose à l’ensemble de ses gérants, ainsi qu’aux gérants de ses gérants, etc., de transmettre à l’ASP toute l’information sur leurs positions.
On est ainsi de fait passé de la notion de » transparence des risques » à celle de » transparence des positions « , au prix de l’établissement d’un monopole de fait.
Rendre le risque additif, sans approximation
Dans tous les cas, les coûts de consolidation viennent en fait du caractère non additif du risque. La solution est donc de rendre le risque additif !
L’intérêt de l’additivé : l’exemple du modèle factoriel
On a vu que les modèles factoriels sont additifs, ce qui rend la problématique de consolidation aussi simple que la consolidation des valeurs.
De même que : prix (A) + prix (B) = prix (A + B).
On a : risque (A) + risque (B) = risque (A + B).
Dans ce cadre, une réelle transparence des risques est possible, de même qu’il existe une réelle transparence comptable, sans qu’il soit nécessaire de dévoiler et de transmettre le détail des positions et engagements financiers. Cette transparence peut se faire au travers de multiples étages de consolidation, comme elle se fait pour les prix : le gérant d’une poche, puis le fonds, puis l’actif global (multifonds) d’un investisseur institutionnel, puis après consolidation avec le passif l’actionnaire, etc.
Le problème des modèles factoriels est qu’ils ne sont pas exhaustifs. Ils n’intègrent pas les non-linéarités, le risque de crédit et les corrélations avec les actifs d’autres marchés.
Un modèle factoriel universel : le risk ticker
Comment faire la synthèse entre une approche factorielle – c’est-à-dire l’idée de représenter un actif par un vecteur additif de chiffres – et les techniques rigoureuses du risk management ?
En d’autres termes, quels sont les facteurs universels, sur lesquels on peut projeter tous les actifs, quels que soient leur type, leur classe, en rendant compte de tous leurs risques spécifiques ? La réponse est en fait très intuitive. Quand on pense au risque, on se pose en réalité la question : que va-t-il se passer demain sur les marchés financiers (ou dans deux semaines ou dans un mois) ?
On pose la question à la manière du risk management, c’est-à-dire non pas en imaginant un scénario possible, mais 1 000 (ou 10 000) scénarios possibles et équiprobables pour la journée de demain, ce pour l’ensemble des marchés financiers.
Ces 1 000 (ou 10 000) scénarios constituent bien nos facteurs universels.
D’abord, je peux projeter tous les actifs, quelles que soient leur nature ou leur complexité, sur ces facteurs : si je sais valoriser un actif aujourd’hui, alors je sais bien calculer ses 1 000 valeurs possibles pour chacun des scénarios de marché imaginés pour demain, quelles que soient la classe ou la complexité de l’actif.
Ensuite, je peux être exhaustif : quand je procède aux 1 000 réévaluations de l’actif, rien ne m’interdit d’inclure tous les risques spécifiques, dès lors qu’ils ont un impact sur la valeur de l’actif – arbitrage, crédit, liquidité, etc.
Enfin, je conserve bien la propriété d’additivité : le vecteur de 1 000 prix possibles se comporte comme un prix.
Cette projection d’un actif sur les 1 000 scénarios constitue un risk ticker, c’est-à-dire une représentation additive, universelle et exhaustive du risque de l’actif.
Une simulation cohérente de l’ensemble des marchés financiers
|
Approche par scénarios : un modèle additif
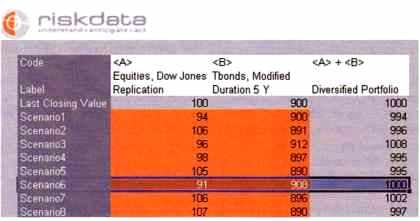
Si dans le scénario n° 6, mon portefeuille Actions A vaut 104 euros et mon portefeuille Obligations B vaut 895 euros, alors mon portefeuille A + B vaut 104 + 895 = 999 euros. Le fait que A et B soient anticorrélés se traduira par le fait qu’en général (mais pas toujours) quand A monte, B baisse, et vice versa : de ce fait la dispersion des valeurs A + B sera moindre que celle des valeurs A ou celle des valeurs B.
|
 |
Cette approche risk ticker n’a en soi rien de révolutionnaire : elle exploite une propriété bien connue des professionnels du risque, qui est l’additivité et la puissance des simulations Monte-Carlo. Elle n’était, jusqu’à récemment, pas réalisable, pour plusieurs raisons.
D’une part, la première génération de systèmes de risque a été conçue dans un environnement où la mémoire et la puissance de calcul restaient coûteuses. Dans ce cadre, représenter un actif par 1 000 chiffres (et les calculer 1 000 fois pour les produits dérivés) aurait été trop coûteux ou trop lent.
D’autre part, une simulation cohérente de l’ensemble des marchés financiers – soit des millions de prix expliqués par des dizaines de milliers de sous-jacents – pose des problèmes très complexes de stabilité et de convergence des algorithmes, et de temps de calcul.
La réduction massive des coûts de la puissance de calcul et de la mémoire, conjuguée aux progrès spectaculaires accomplis ces dernières années en mathématiques financières, a rendu effectivement possible cette simulation globale.
Les résultats enregistrés depuis septembre 2001, date à laquelle la première unité de production de risk tickers a été lancée, ont permis à ses premiers utilisateurs de confirmer qu’ils tenaient avec le concept de risk ticker la solution permettant de répondre de manière précise, fiable et économique à la demande de transparence des risques.