Intrication et calcul quantique


Le XXe siècle a connu deux révolutions quantiques : celle de la mécanique quantique et de la dualité onde-particule puis celle de l’intrication. Cette deuxième révolution ouvre la porte à la création d’ordinateurs quantiques, considérés comme le graal du monde informatique.
À partir des années 1960 une seconde révolution quantique a émergé, basée sur un concept encore plus étonnant : l’intrication. À la différence de la première révolution quantique qui reposait sur l’application statistique des concepts quantiques à un très grand nombre d’objets élémentaires (électrons, atomes ou photons), la seconde révolution concerne le comportement individuel d’un petit nombre d’objets quantiques.
Elle est liée au développement de techniques expérimentales extraordinaires qui ont permis de capturer, d’observer et de contrôler des électrons, des ions ou des atomes uniques, d’émettre des photons un par un, ou paire intriquée après paire intriquée.
Des comportements étonnants, discutés auparavant dans des expériences de pensée, sont devenus l’objet d’investigations expérimentales et théoriques. Cette seconde révolution quantique est maintenant sollicitée pour ouvrir la porte à l’information quantique.
REPÈRES
La mécanique quantique a été une révolution scientifique majeure du XXe siècle. Basée sur le concept contre-intuitif de dualité onde-particule, la première révolution quantique a d’abord permis de comprendre la structure de la matière.
Elle a ensuite conduit au transistor et à la microélectronique, au laser et aux télécommunications optiques, aux horloges atomiques et au GPS, c’est-à-dire aux bases technologiques de la société de l’information et de la communication.
INFORMATION ET ORDINATEUR QUANTIQUES
Selon la célèbre maxime de Rolf Landauer, l’information est de nature physique. Un support quantique de l’information doit donc permettre la transmission et le traitement quantique de cette information, avec des règles du jeu différentes de celles connues classiquement.
Les chercheurs ont accès à de nouvelles méthodes de cryptographie, dont la sécurité s’appuie sur les bases mêmes de la physique, ou à de nouvelles méthodes de calcul, qui peuvent être exponentiellement plus efficaces.
En ce qui concerne la sécurité de la transmission des données, la cryptographie quantique est une technologie bien maîtrisée, avec de premiers systèmes commerciaux. Il est maintenant possible de distribuer des « clés secrètes », avec des débits atteignant 1 Mbit/s pour des distances de l’ordre de 50 kilomètres.
Avec des relais réputés sûrs séparés par quelques dizaines de kilomètres, les réseaux cryptés peuvent atteindre des distances arbitraires. Des liaisons sécurisées sans sites intermédiaires sont à l’étude, en utilisant des satellites, ou une méthode appelée téléportation quantique.
UN CONCEPT RÉVOLUTIONNAIRE
L’ordinateur quantique est l’objet de recherches intenses dans le champ académique, avec une implication forte et croissante de grandes compagnies industrielles. Le concept d’ordinateur quantique, mettant en jeu de nouvelles règles de calcul basées sur les superpositions d’état et l’intrication, est effectivement révolutionnaire.
Des théoriciens de l’information, de l’algorithmique, et de la théorie de la complexité, se sont emparés des nouvelles règles pour imaginer de nouveaux algorithmes et de nouvelles architectures de calcul, basées sur des portes quantiques sans équivalent classique.
La rencontre entre la théorie de l’information et la mécanique quantique renouvelle les outils théoriques utilisés de part et d’autre et suggère aussi de nouvelles approches des fondements de la théorie quantique.
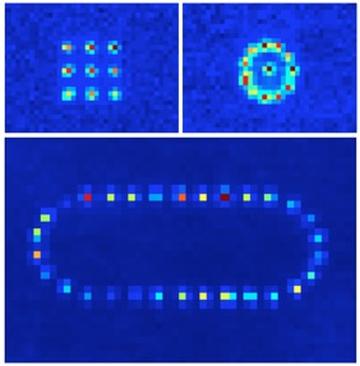
SOURCE : LABORATOIRE CHARLES FABRY, PALAISEAU
DU BIT AU QUBIT
La mise en œuvre pratique du calcul quantique progresse aussi remarquablement, mais plus lentement. De nombreux systèmes sont étudiés en tant que supports de l’unité quantique d’information, le qubit.
Un qubit peut être soit dans l’état zéro soit dans l’état un, comme un bit classique, mais aussi dans une superposition quantique de ces deux états. Il faut de plus pouvoir intriquer ces bits quantiques, c’est-à-dire pouvoir créer des superpositions quantiques de registres contenant plusieurs qubits.
Les premiers qubits ont été naturels (cf. supra) : photons polarisés, atomes et ions piégés, spins nucléaires d’atomes piégés, inclus dans des molécules, implantés dans des semi-conducteurs, des nanotubes de carbone, du diamant, etc.
Mais se développent aussi des qubits artificiels (cf. infra), comme les systèmes supraconducteurs à quantum de flux ou de charge. Un enjeu majeur est de manipuler ces systèmes sans détruire leur « cohérence quantique », associée en particulier à l’intrication.
Le problème devient crucial lorsqu’il s’agit d’assembler un grand nombre de qubits, et il faut insister sur l’importance des codes correcteurs quantiques qui ont été conçus pour préserver la cohérence des qubits.
La mise en œuvre expérimentale de ces codes correcteurs progresse à grands pas, et le nombre de qubits disponibles dans les systèmes les plus avancés (jusqu’à une vingtaine) devrait permettre une démonstration de principe dans un futur proche .
L’assemblage à grande échelle de qubits capables d’effectuer des calculs protégés des erreurs demeure néanmoins un défi majeur. Même si un assemblage de qubits supraconducteurs est commercialisé par la compagnie canadienne D‑Wave, une réelle accélération quantique dans un calcul n’a pas encore été démontrée de manière indiscutable.
LES PREMIERS SIMULATEURS QUANTIQUES
Au stade actuel, les premiers résultats utiles du calcul quantique devraient provenir des simulateurs quantiques, proposés par Feynman dans son article fondateur de 1982. Il s’agit de laisser la nature calculer pour nous, en réalisant des expériences sur des systèmes parfaitement contrôlés, par exemple des atomes ultra-froids placés dans des potentiels lumineux.
Suivant la structure périodique ou désordonnée de ces potentiels, les atomes simulent la physique des électrons dans un cristal, ou dans un matériau amorphe comme un verre. Il est aussi possible de capturer des atomes individuels dans des pièges de géométrie arbitraire, et de les faire interagir entre eux.
L’ordinateur quantique associe donc des concepts révolutionnaires au développement de technologies qui s’efforcent de devenir une ingénierie quantique. Il n’existe pas encore d’ordinateur quantique plus rapide que tout calculateur classique, mais cette possibilité attire l’intérêt de nombreux mathématiciens, physiciens, informaticiens, biologistes, etc., et aussi des grandes compagnies de l’informatique et d’Internet.
En parallèle, les nouvelles technologies quantiques résultant de ces études sont utilisées pour dépasser les limites usuelles de précision dans la métrologie des temps ou des fréquences, des longueurs ou des angles, de la gravitation, des champs magnétiques, etc. La liste ne sera limitée que par l’imagination des physiciens et des ingénieurs
RÉFÉRENCES BIBLIOGRAPHIQUES
A. ASPECT – « Une nouvelle révolution quantique », in É. Brézin et S. Balibar (dir.), Demain, la Physique, Odile Jacob, 2009.
À propos du calcul quantique, deux vidéos :
PETIT GLOSSAIRE QUANTIQUE
Dualité onde-particule
Les états accessibles à un système quantique incluent la possibilité de « superpositions quantiques », qui sont d’autres états associés à d’autres mesures possibles. Par exemple il est possible de superposer des amplitudes de probabilités associées aux deux chemins possibles d’une particule dans un interféromètre, ce qui se manifeste par l’apparition de propriétés ondulatoires (interférences) de cette particule.
Intrication
Il est possible de faire des superpositions quantiques d’états impliquant plusieurs particules : on a alors des états « globaux », dans lesquels il n’est plus possible d’attribuer un état bien défini à chaque particule. Ces états présentent des propriétés particulières de non-localité quantique, qui se traduisent expérimentalement par la possibilité de violer les « inégalités de Bell », contraignant toute description « réaliste locale » d’inspiration classique.
Téléportation quantique
Lorsqu’on dispose de deux particules intriquées 1 et 2 séparées spatialement, il est possible de « téléporter » l’état d’une troisième particule, en détruisant cet état (ainsi que celui de la particule 1), mais en le récréant sur la particule 2. Cette transmission n’est pas instantanée, mais elle est « parfaitement sûre » d’un point de vue cryptographique, c’est-àdire que l’état téléporté n’est pas « lisible » par un espion extérieur.
Qubit
Unité d’information quantique, qui possède deux états mutuellement exclusifs 0 et 1 comme un bit classique, mais qui a aussi accès à toutes les superpositions quantiques de ces états 0 et 1.
Portes quantiques
Il s’agit de portes logiques quantiques, c’est-à-dire d’opérations logiques effectuées entre qubits. Elles sont toujours réversibles, donc le nombre de qubits reste le même avant et après l’action de la porte (ce n’est en général pas le cas pour une porte classique, par exemple les portes classiques « ET » ou « OU » ont deux bits en entrée, et un seul bit en sortie). La porte quantique « NON contrôlé » est une version réversible de la porte « OU exclusif », avec deux qubits en entrée et deux en sortie, et elle peut bien sûr agir sur des superpositions quantiques de 0 et de 1. La porte « NON » classique (ou quantique) transforme 0 en 1 et 1 en 0, et la porte quantique « racine de NON » est telle qu’on obtient une porte NON en l’appliquant deux fois de suite. Elle n’a pas d’équivalent classique.
Accélération quantique (quantum speed-up)
Possibilité pour un ordinateur quantique d’exécuter certains algorithmes (bien choisis) plus rapidement que n’importe quel calculateur classique. Une démonstration concrète de cette accélération, même pour un algorithme peu utile en pratique comme le « boson sampling », est un gros enjeu en information quantique.
Photons polarisés
Un photon est un quantum d’énergie du champ électromagnétique, et c’est un très bon qubit, qui peut se propager sur de grandes distances en portant l’information sur sa polarisation (analogue à une direction de vibration). Il est difficile de réaliser des portes logiques entre qubits photoniques, mais de nombreuses méthodes sont actuellement explorées.
Atomes et ions piégés
Atomes ou ions individuels, que l’on peut contrôler dans des pièges électromagnétiques (ions) ou lumineux (atomes). Les qubits ioniques sont actuellement mieux contrôlés, mais par contre il est plus facile d’avoir un grand nombre de qubits atomiques, en particulier dans des structures bidimensionnelles.
Qubits artificiels
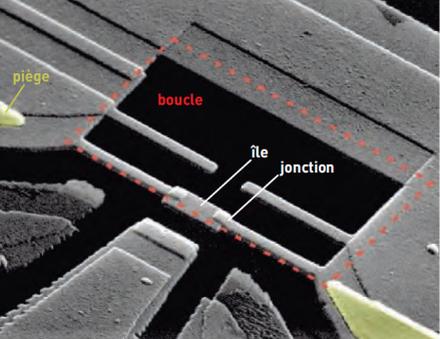
À la différence des qubits basés sur des ions ou des atomes, ce sont des circuits supraconducteurs, impliquant le plus souvent des jonctions Josephson, et une quantification du flux ou de la charge. On peut ainsi obtenir un qubit de très bonne qualité, mettant en jeu collectivement un nombre élevé d’électrons, et ces systèmes semblent très prometteurs.
Théorie de la complexité
Branche des mathématiques dont l’objectif est de catégoriser la difficulté des algorithmes de calcul ou de traitement des données.
Spins nucléaires
Les noyaux des atomes ont en général un moment magnétique (ce sont de petits aimants), associé à une valeur non nulle de leur spin (moment cinétique intrinsèque).
Supraconducteurs
À température très basse la résistance électrique de certains matériaux peut s’annuler ; on dit alors qu’ils deviennent supraconducteurs.
Quantum de flux ou de charge
Dans un supraconducteur les valeurs du courant, de la charge, ou du flux magnétique peuvent prendre des valeurs discrètes, ou quantifiées. Ces grandeurs physiques sont alors susceptibles de « porter » des qubits (voir ce mot).
Atomes ultra-froids
Atomes dont l’énergie cinétique a été diminuée par diverses méthodes (refroidissement laser, refroidissement évaporatif), jusqu’à atteindre des températures cinétiques dans la gamme du μK (millionième de degré Kelvin).
Potentiels lumineux
Un faisceau lumineux modulé en intensité, par exemple à cause d’effets d’interférences, peut exercer un effet mécanique sur des atomes. Il apparaît ainsi comme un potentiel, avec des minima et maxima, susceptible de piéger les atomes dans des « puits » d’énergie potentielle.