Biomédecine et physique : Mouvements collectifs de micronageurs confinés

L’essor de nou­velles tech­niques de micro­scopie et de micro­ma­nip­u­la­tion a per­mis dans les dernières décen­nies des avancées spec­tac­u­laires dans l’étude des nageurs micro­scopiques, en par­ti­c­uli­er celle des bac­téries. De nom­breuses ques­tions per­sis­tent cepen­dant quand l’environnement de ces nageurs est com­plexe, par exem­ple en présence de parois ou d’autres nageurs. Le présent tra­vail allie expéri­ences et théorie pour analyser le com­porte­ment d’une sus­pen­sion con­finée de bac­téries mag­né­to­tac­tiques, avec des appli­ca­tions en biolo­gie et en ingénierie médi­cale. 

Dans Le Voy­age fan­tas­tique, film de sci­ence-fic­tion de 1966, le sous-marin Pro­teus et son équipage sont minia­tur­isés et injec­tés dans le corps d’un sci­en­tifique : ils ont une heure pour détru­ire un cail­lot dans son cerveau et le sauver. 

Micronageurs : de la fiction à la médecine ? 

Les effets spé­ci­aux qui illus­trent le monde micro­scopique de notre organ­isme et les dan­gers qui y rôdent ont valu à l’équipe du film deux Oscars. Mais qu’en diraient un médecin, un biol­o­giste ou un physi­cien ? Quelques heures dans les salles obscures ont déjà pu suf­fire à vous con­va­in­cre qu’Hollywood ne va pas de pair avec la rigueur sci­en­tifique. Une telle minia­tur­i­sa­tion, en par­ti­c­uli­er, est irréal­is­able : en physique, la taille car­ac­téris­tique d’un sys­tème compte. On ne peut pas réduire ou grossir arbi­traire­ment un objet tout en con­ser­vant ses pro­priétés et son fonc­tion­nement. Ain­si, et nous y revien­drons, les lois qui régis­sent les flu­ides à l’échelle macro­scopique et à l’échelle micro­scopique ne sont pas les mêmes. Et pour­tant : l’idée d’injecter dans le corps d’un patient un nageur micro­scopique con­trôlé de l’extérieur pour des opéra­tions moins inva­sives que par des moyens clas­siques n’est pas réservée aux pro­duc­teurs de ciné­ma. Elle est l’objet d’une recherche bio­médi­cale pluridis­ci­plinaire dont les appli­ca­tions envis­agées sont nom­breuses. Comme dans Le Voy­age fan­tas­tique, on imag­ine déloger les cail­lots san­guins, mais aus­si réalis­er des chirur­gies artérielles plus complexes. 

Si le nageur peut trans­porter des médica­ments jusqu’à une zone déter­minée, des traite­ments locaux pour­raient être élaborés, notam­ment pour s’attaquer de façon ciblée aux tumeurs can­céreuses. De tels robots sont déjà dévelop­pés dans de nom­breux lab­o­ra­toires et leurs con­cep­teurs cherchent à les ren­dre plus petits, plus pré­cis, plus con­trôlables. Pour­tant, leur réal­i­sa­tion soulève de nom­breuses ques­tions : quelle sera la réponse du sys­tème immu­ni­taire à leur présence ? Com­ment les fab­ri­quer de manière repro­ductible et peu coû­teuse ? Après leur util­i­sa­tion, com­ment seront-ils dégradés ou évac­ués ? Leur motil­ité (i.e. leur capac­ité à se déplac­er con­tinû­ment dans un liq­uide en défor­mant leur corps) pose en par­ti­c­uli­er des prob­lèmes fon­da­men­taux, abor­dés dans la présente thèse : com­ment parviendraient-ils à se déplac­er, s’orienter, éviter les obsta­cles et inter­a­gir effi­cace­ment avec d’autres nageurs ? 

De la difficulté de nager à l’échelle microscopique

Pour mieux appréhen­der les enjeux de la nage à l’échelle micro­scopique, nous devons revenir à la dif­férence, évo­quée plus haut, entre un flu­ide à l’échelle macro­scopique, celle des océans, des lacs, des piscines, mais aus­si d’un verre d’eau, et un flu­ide à l’échelle micro­scopique, celle d’une goutte d’huile, de nos capil­laires san­guins, des cel­lules. La pre­mière nous est bien plus famil­ière ; et pour­tant c’est dans la deux­ième qu’évoluent la plu­part des êtres vivants de la pièce où vous vous trou­vez. 

En général, le com­porte­ment d’un flu­ide est régi par l’inertie et la vis­cosité. La pre­mière cor­re­spond au fameux terme « masse fois accéléra­tion » des équa­tions de New­ton, qui rend la chute d’une pomme sur la tête dudit New­ton plus douloureuse si le pom­mi­er est haut. La vis­cosité est une grandeur plus élu­sive, qui mesure la résis­tance d’un liq­uide à l’écoulement : l’acétone ou l’eau ont une vis­cosité faible, alors que celle de la gly­cérine ou de la résine est élevée. Le nom­bre de Reynolds per­met de com­par­er l’importance rel­a­tive de l’inertie et de la viscosité. 

Pour l’évaluer, con­sid­érons un nageur de taille L, qui se déplace à une vitesse U, dans un flu­ide car­ac­térisé par sa den­sité ρ et sa vis­cosité µ. Le nom­bre de Reynolds est le ratio adi­men­sion­nel des forces iner­tielles et visqueuses : Re = ρUL/µ. Dans le monde micro­scopique, U et L étant très petites, ce nom­bre de Reynolds est très inférieur à un et l’inertie dis­paraît : l’environnement est entière­ment régi par les forces visqueuses. On notera qu’un très petit nom­bre de Reynolds peut aus­si exis­ter à de très grandes tailles : il suf­fit pour cela que la vis­cosité du liq­uide soit très élevée. C’est le cas dans le man­teau ter­restre, dont la vis­cosité est 10²⁴ plus élevée que celle de l’eau ! Les forces grav­i­ta­tion­nelles de la Terre ont beau être immenses, l’écoulement du man­teau reste très lent et dom­iné par la vis­cosité. 

Le nom­bre de Reynolds pour un nageur dans une piscine est de l’ordre de 10⁴ ; pour les micronageurs biologiques que nous étu­dions, comme les bac­téries et les sper­ma­to­zoïdes, il est de 10^-4. Alors, à quoi ressem­ble la vie à très bas nom­bre de Reynolds ? Edward Mills Pur­cell, dans une con­férence de 1977, pro­po­sait l’analogie suiv­ante : vous êtes dans une piscine de mélasse, et de plus vous ne pou­vez bouger votre corps qu’à 1 cm/min, si bien que vos mou­ve­ments de bras ne dépassent pas la vitesse des aigu­illes d’une hor­loge. Si dans ces con­di­tions vous par­venez à vous déplac­er de plusieurs mètres en quelques jours, vous êtes bien un nageur à bas nom­bre de Reynolds. 

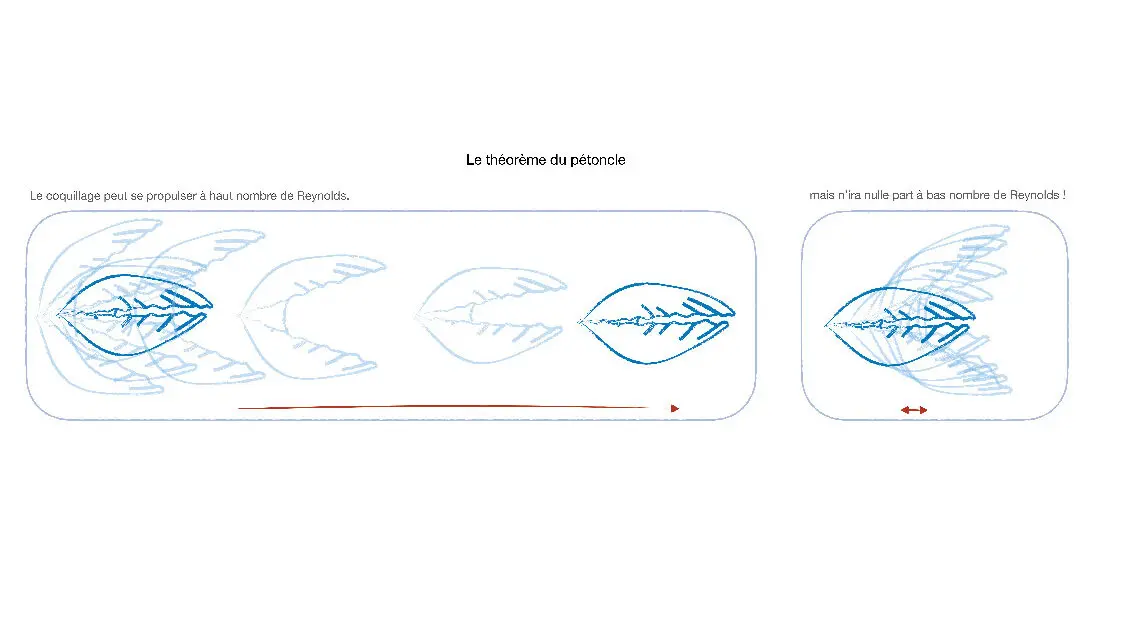
La per­for­mance n’est pas anodine, puisque l’inertie représente la capac­ité à avancer encore quand nous arrê­tons de bouger, par exem­ple après la poussée con­tre le mur d’une piscine. Elle est inex­is­tante pour une bac­térie : si celle-ci arrête de nag­er, elle s’immobilise après 0,1 angström – la taille d’un atome. Son déplace­ment est entière­ment déter­miné par son action présente, et par rien de ce qui est arrivé dans le passé : la nage est instan­ta­née. Se mou­voir est d’autant plus dif­fi­cile que l’absence d’inertie a une con­séquence addi­tion­nelle : un mou­ve­ment réversible (i.e. iden­tique si le temps avance ou remonte) ne peut con­duire à aucun déplace­ment. Aucune mod­u­la­tion de rythme ne peut y remédi­er : cette pro­priété est surnom­mée « théorème du péton­cle » et est illus­trée ci-dessous. Ni le bat­te­ment des nageoires, ni celui des ailes, ni le mou­ve­ment d’une coquille ou l’expulsion de l’eau du corps d’une méduse ne per­met de quit­ter le point de départ. 

Stratégies de nage microscopique

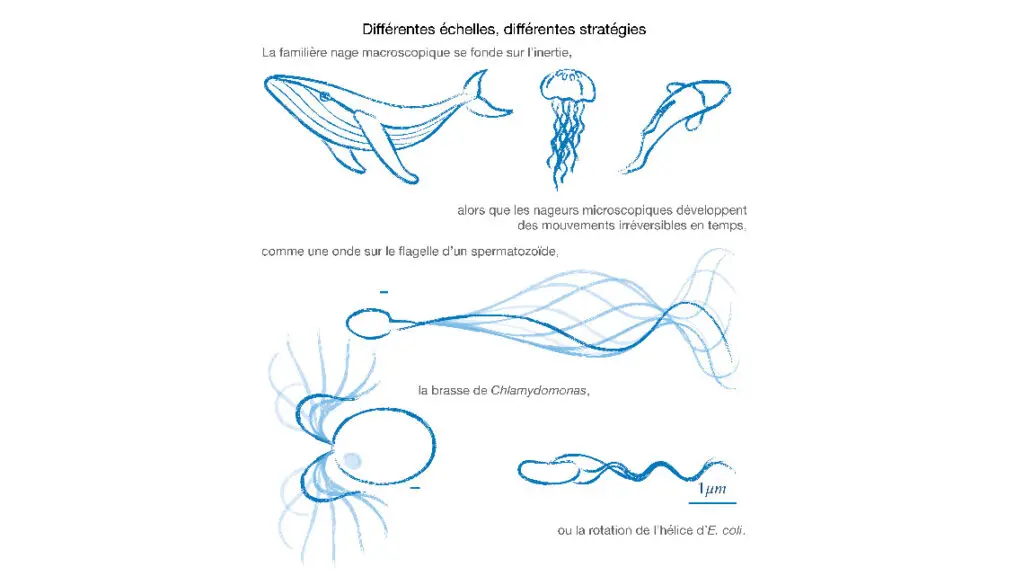
Une stratégie de nage à l’échelle macro­scopique sera inap­plic­a­ble à l’échelle micrométrique. Mais alors, com­ment se déplac­er ? L’image ci-après donne quelques exem­ples de nage micro­scopique, dont le point com­mun est de bris­er la symétrie entre le mou­ve­ment exé­cuté à l’endroit, vu en marche avant, et à l’envers, en marche arrière. Cer­tains planc­tons utilisent des fla­gelles qu’ils défor­ment en mou­ve­ments non réversibles, comme la brasse de l’algue verte Chlamy­domonas rein­hardtii. Les sper­ma­to­zoïdes, eux, exploitent l’asymétrie d’une onde qui se propage de leur queue vers leur tête. Les bac­téries, enfin, pos­sè­dent un ou plusieurs appendages rigides, en forme d’hélice, dont la rota­tion dans le sens con­traire des aigu­illes d’une mon­tre per­met un mou­ve­ment net. L’efficacité de la nage bac­téri­enne est remar­quable : E. coli, quand elle nage, se déplace à plus de 20 µm/s, soit env­i­ron qua­tre fois sa taille à chaque sec­onde, plus vite rel­a­tive­ment qu’un nageur olympique ou même un dauphin. 

L’étude des nageurs micro­scopiques, en par­ti­c­uli­er celle des bac­téries, a pris son essor dans les années 2000 grâce à l’avènement de tech­niques de micro­scopie qui ont per­mis d’observer pour la pre­mière fois les fla­gelles de bac­téries. Si leur nage en milieu homogène est depuis lors bien car­ac­térisée, de nom­breuses ques­tions per­sis­tent quand l’environnement est plus com­plexe, par exem­ple en présence d’autres nageurs ou de parois. Or la plu­part des micro-organ­ismes évolu­ent dans de tels milieux, comme l’humus ter­restre ou le corps humain pour les appli­ca­tions médi­cales. L’objet de ma thèse est juste­ment de pro­pos­er des mod­èles valides pour les micronageurs con­finés, en par­ti­c­uli­er pour les sus­pen­sions, qui désig­nent un grand nom­bre de nageurs dis­per­sés dans un même liq­uide. La suite de cet arti­cle présente une par­tie de ce tra­vail, qui s’est con­cen­tré sur des sus­pen­sions de bac­téries dites mag­né­to­tac­tiques. 

Se diriger grâce aux champs magnétiques

Ces bac­téries ont une pro­priété sin­gulière : elles s’orientent en suiv­ant les champs mag­né­tiques de leur envi­ron­nement. En effet, elles pos­sè­dent dans leur corps des nano-aimants, appelés mag­né­to­somes. Un champ extérieur crée un moment qui aligne ces aimants et donc le corps de la bac­térie, avec lui. La force exer­cée étant nég­lige­able, la vitesse de la bac­térie est con­trôlée par sa nage, mais elle est ori­en­tée par le champ extérieur. Une pos­si­ble expli­ca­tion à ce com­porte­ment est l’utilité pour une bac­térie de se guider en util­isant le champ mag­né­tique ter­restre, puisque la grav­ité est nég­lige­able et que les bac­téries ne peu­vent dis­tinguer le haut du bas ou de toute autre direc­tion dans leur envi­ron­nement. 

Le mag­né­to­tac­tisme est promet­teur pour de nom­breuses appli­ca­tions puisqu’il per­met de guider un nageur avec un champ inof­fen­sif pour un être humain, soit en util­isant directe­ment les bac­téries, soit en con­férant la même pro­priété à un nageur arti­fi­ciel. Il mod­i­fie cepen­dant de manière sig­ni­fica­tive le com­porte­ment des nageurs, tant pour un nageur isolé que pour une sus­pen­sion, ce qui requiert un tra­vail spé­ci­fique pour mod­élis­er et prédire leur com­porte­ment. Par exem­ple, puisqu’ils sont guidés par le champ mag­né­tique plutôt que par les pro­priétés locales de leur envi­ron­nement, ils ont ten­dance à s’accumuler con­tre des obsta­cles et des parois. 

Comment des bactéries magnétotactiques interagissent-elles avec leur environnement ? 

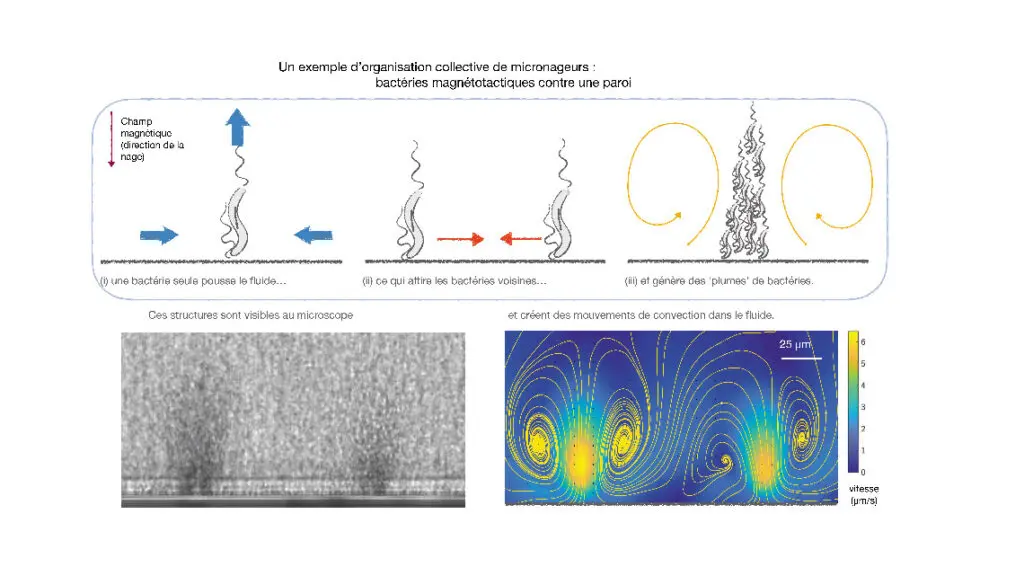
Notre tra­vail allie des expéri­ences et un mod­èle pour analyser le com­porte­ment d’une sus­pen­sion de bac­téries mag­né­to­tac­tiques. De nom­breuses bac­téries sont intro­duites dans un capil­laire en verre à sec­tion car­rée, puis nous générons un champ mag­né­tique per­pen­dic­u­laire à l’axe du tube. Ce dis­posi­tif nous per­met d’observer l’accumulation de bac­téries mag­né­to­tac­tiques con­tre l’une des parois et de mesur­er la cir­cu­la­tion du flu­ide dans le capil­laire. Plutôt qu’en une couche uni­forme de bac­téries qui nageraient per­pen­dic­u­laire­ment au mur, nous obser­vons rapi­de­ment la for­ma­tion de « plumes » per­pen­dic­u­laires à la paroi. Ces plumes créent des recir­cu­la­tions sem­blables à de larges cel­lules de con­vec­tion, qui gran­dis­sent jusqu’à attein­dre la taille du capil­laire. 

“Le magnétotactisme est prometteur pour de nombreuses applications.”

Ce phénomène d’accumulation locale de nageurs peut être décrit par un mod­èle hydro­dy­namique sim­ple. Lorsqu’elle nage con­tre une paroi, une bac­térie ne peut pas bouger et se con­tente alors d’expulser du flu­ide der­rière elle. Tout se con­serve, en par­ti­c­uli­er la masse du flu­ide envi­ron­nant : cette expul­sion vers l’arrière est com­pen­sée par l’arrivée de liq­uide sur les côtés, comme sur le sché­ma ci-con­tre. Lorsque plusieurs bac­téries poussent ain­si con­tre le mur, elles attirent donc le flu­ide autour d’elle et, avec lui, leurs voisines. De petits groupes se for­ment et se regroupent à leur tour. Lorsqu’ils atteignent une taille cri­tique, le flu­ide qu’ils expulsent vers l’arrière entraîne des bac­téries, d’où la for­ma­tion de plumes allongées per­pen­dic­u­laires au mur. 

La cir­cu­la­tion de flu­ide déplacé par la nage des bac­téries crée en retour les struc­tures que nous obser­vons dans le flu­ide. Cette attrac­tion entre bac­téries voisines et l’organisation de la sus­pen­sion qui en découle ne peu­vent avoir lieu qu’en présence du champ mag­né­tique. Si le champ est éteint, ou que les bac­téries ne s’alignent pas, la solu­tion reste uni­forme et désor­don­née. Notre tra­vail a ain­si per­mis de mon­tr­er que l’existence d’un mécan­isme d’orientation externe aux nageurs, mag­né­tique ou non, trans­forme rad­i­cale­ment l’interaction des bac­téries avec les parois de leur envi­ron­nement. 

À l’échelle microscopique, les petits détails comptent

D’autres expéri­ences obser­vaient les bac­téries dans une goutte sphérique plutôt que con­tre une paroi. Bien que les deux sys­tèmes soient très proches, leurs com­porte­ments sont très dif­férents : les bac­téries créent un vor­tex d’axe ver­ti­cal et la goutte se met à tourn­er dans le sens des aigu­illes d’une mon­tre. C’est cette dernière pro­priété, une rota­tion avec une direc­tion définie, qui nous a le plus intrigués : pourquoi tourn­er dans ce sens et non par­fois dans le sens horaire et par­fois dans l’autre, comme le prédi­s­ait le mod­èle que nous avions dévelop­pé ? Nous avons alors mon­tré que la cour­bu­re des parois de la goutte per­me­t­tait d’observer un autre phénomène, jusqu’alors nég­ligé : la chi­ral­ité du fla­gelle de la bac­térie. 

La chi­ral­ité, du grec kheir – main, est la pro­priété d’un objet qui n’est pas super­pos­able à sa réflex­ion dans le miroir : une main ou, ici, une hélice. Cette chi­ral­ité est trans­mise, de par la rota­tion de l’hélice, au flu­ide autour d’une bac­térie ou d’un groupe de bac­téries, et influe sur leur inter­ac­tion avec une paroi courbe ou inclinée. La rota­tion de tous les fla­gelles dans le même sens, cou­plée à la géométrie de l’environnement et à la grav­ité, est finale­ment trans­mise à la goutte entière et la fait tourn­er dans le sens horaire. Cette pro­priété micro­scopique dev­enue dom­i­nante à l’échelle de la goutte doit donc être prise en compte dans nos mod­èles de nage dans des géométries com­plex­es. À cette échelle, même les plus petits détails comptent ! 

En somme, notre tra­vail a per­mis de mieux com­pren­dre le rôle d’une ori­en­ta­tion externe dans le com­porte­ment de groupes de micronageurs, avec des appli­ca­tions pos­si­bles en biolo­gie et en ingénierie médi­cale. Plus large­ment, il s’agit d’un exem­ple des prob­lèmes inter­dis­ci­plinaires très rich­es qui se posent en biolo­gie et peu­vent être abor­dés avec les out­ils de la physique et de la mécanique clas­sique. Récipro­que­ment, le monde vivant génère une pro­fu­sion de nou­velles ques­tions en mécanique des flu­ides, avec un cadre très dif­férent des ques­tions clas­siques d’ingénierie, comme ici les flu­ides à très petites échelles. C’est sur ces ques­tions que por­tent l’ensemble de ma thèse et ma recherche actuelle. 

Ressources

• E.M. Pur­cell, Life at low Reynolds num­ber, Amer­i­can Jour­nal of Physics 45,3 (1977). https://doi.org/10.1119/1.10903
• B. Vicen­ti, G. Ramos, M.L. Cordero, C. Douarche, R. Soto et É. Clé­ment, Mag­ne­to­tac­tic bac­te­ria in a droplet self-assem­ble into a rotary motor, Nature com­mu­ni­ca­tions 10, arti­cle n° 5082 (2019). https://doi.org/10.1038/s41467-019–13031‑6
• A. Théry, L. Le Nagard, J.-C. Ono-dit-Biot, C. Fradin, K. Dal­no­ki-Ver­ess, E. Lau­ga. Self-organ­i­sa­tion and con­vec­tion of con­fined mag­ne­to­tac­tic bac­te­ria. Sci­en­tif­ic Reports 10, arti­cle n° 13578 (2020). https://doi.org/10.1038/s41598-020–70270‑0

Informations sur la thèse 

Le tra­vail présen­té ici a été réal­isé dans le cadre d’une thèse en math­é­ma­tiques appliquées à l’Université de Cam­bridge inti­t­ulée Con­fine­ment-medi­at­ed accu­mu­la­tion and col­lec­tive dynam­ics of microswim­mers (Accu­mu­la­tion et organ­i­sa­tion col­lec­tive de micronageurs con­finés). La thèse a été soutenue en mai 2022, le jury de thèse était com­posé de Ray­mond E. Gold­stein (Uni­ver­sité de Cam­bridge) et Cécile Cot­tin-Bizonne (Insti­tut Lumière Matière, Lyon).

https://doi.org/10.17863/CAM.85810

Laboratoire d’accueil

Cette thèse a été réal­isée dans le groupe d’Éric Lau­ga au DAMTP (Départe­ment de Math­é­ma­tiques Appliquées et Physique Théorique) de l’Université de Cam­bridge au Roy­aume-Uni. Elle a été financée par une ERC de l’Union Européenne attribuée à Éric Lau­ga dans le cadre du pro­gramme Hori­zon 2020. L’activité de recherche du groupe est cen­trée sur le développe­ment de mod­èles quan­ti­tat­ifs pour les nou­velles ques­tions en mécanique des flu­ides biologiques, grâce à une com­bi­nai­son de mod­èles ana­ly­tiques, d’analy­ses asymp­to­tiques et de sim­u­la­tions numériques. Les prob­lèmes étudiés inclu­ent la loco­mo­tion dans des flu­ides visqueux, ain­si que la mod­éli­sa­tion des flu­ides biologiques à l’échelle cel­lu­laire, et de mul­ti­ples prob­lèmes d’hydrodynamique physique à petite échelle.

https://www.damtp.cam.ac.uk/user/lauga/index.html

Les expéri­ences décrites ci-dessus ont été réal­isées dans le lab­o­ra­toire de Kari Dal­no­ki-Ver­ess, au Départe­ment de Physique et Astronomie de l’Université McMas­ter, au Cana­da. Elles ont été réal­isées par AT, Lucas Le Nagard, Jean-Christophe Ono-dit-Biot, sous la super­vi­sion de Cécile Fradin et Kari Dalnoki-Veress.

http://kdvlab.net/kdv

---

Articles similaires :

La rece­herche médi­cale et sa valorisation On a détec­té les ondes gravitationnelles Com­po­si­tion de physique — ses­sion de print­emps — ver­sion française Guer­bet, un nou­veau leader de l’imagerie médicale La mod­éli­sa­tion mécanique en car­di­olo­gie : vers le patient virtuel Den­tal­Moni­tor­ing : la licorne qui révo­lu­tionne l’orthodontie et la dentisterie