Covid-19 en 2021
Quelles mesures privilégier pour éviter d’être submergés en mars avril par l’arrivée d’une 3e vague due au variant « anglais » ?
Comparaison entre l’efficacité de différentes options
Théoriquement, le remplacement progressif du virus « 2020 » par un variant « anglais » nettement plus contagieux risque de provoquer l’arrivée d’une 3e vague capable de submerger le système hospitalier. L’expérience de 2020 prouve qu’il est possible de contrecarrer une telle évolution, mais quelles sont les mesures les plus efficaces pour y arriver ? Accélération des vaccinations ? Quarantaines ? Couvre-feux ou confinements, généraux ou localisés ?
À partir du modèle épidémiologique le plus simple, le SIR de Kermack et McKendrick (1927) où une équation inadaptée aux évolutions fortement dynamiques a été corrigée (voir notre article de la J&R en ligne de février) il est possible de reconstituer l’évolution de la Covid-19 depuis son arrivée en France début 2020 et de répondre à cette question sans avoir de connaissances particulières en mathématiques.
Savoir utiliser un tableur de type Excel suffit
Remarques importantesL’article étudie les effets opposés de la vaccination et de l’apparition d’un variant « anglais » nettement plus contagieux que le Covid-19 de 2020. Il compare l’efficacité d’actions permettant de limiter le nombre maximal d’infections (attendu pour avril 2021) à un niveau compatible avec les capacités du système hospitalier national. Il ne prévoit pas la sortie finale de crise, celle qui (espérons-le !) permettra le retour à un mode de vie comparable à celui que nous avons connu jusqu’en février 2020. Mais attention ! Actuellement un virus de coefficient R0 égal à 3 dans les conditions que nous connaissions avant le début de l’épidémie est en train d’être remplacé par un variant pour lequel, dans les mêmes conditions, R0 = 4,5. Ceci fait passer la population minimale devant théoriquement être immunisée (par vaccination, immunité acquise suite à une guérison ou éventuelle immunité innée) de 67% à 78% de la population totale pour voir commencer le reflux spontané de l’épidémie (calcul approximatif basé sur l’équation du SIR de 1927 non corrigée et ne tenant pas compte de l’hétérogénéité entre contaminateurs). Les nombres de nouvelles infections annoncés quotidiennement par les pouvoirs publics correspondent aux seules infections constatées par des tests. En 2021, le nombre réel d’infections (détectées ou non détectées, symptomatiques ou asymptomatiques) est vraisemblablement environ deux fois plus important (au printemps 2020, ce rapport était beaucoup plus élevé, compte tenu de la pénurie de tests). |
Chiffres quotidiens début mars 2021
Nouvelles infections : environ 50 000 par jour dont 50 % constatées par des tests
Par rapport au nombre total d’infections :
- Admissions à l’hôpital : 2,5 % du nombre total d’infections
- Admissions en réanimation, en moyenne 1 semaine après infection : 0,4 %
- Décès, en moyenne 2 semaines après infection : 0,5 %
Document du 23 février traitant du même sujet : « A race between SARS-CoV‑2 variants and vaccination : the case of the B.1.1.7 variant in France » par Paolo Bosetti, Cécile Tran Kiem, Alessio Andronico, Juliette Paireau, Daniel Levy Bruhl, et al.
https://hal.archives-ouvertes.fr/pasteur-03149525
A noter qu’à la différence de ce document, notre article n’inclut pas l’effet d’éventuelles mesure de relâchement de la distanciation physique de la population après le pic d’avril.
Covid-19 en 2021
Influences contraires de la vaccination et du variant « anglais »
Une campagne de vaccination a commencé début 2021, et un couvre-feu à partir de 18 heures est entré en vigueur à la mi-janvier. Ces mesures seront-elles suffisantes pour éviter une 3ème vague due au remplacement progressif du virus « 2020 » par un variant « anglais » plus contagieux ? Que disent les courbes générées par un tableur de type Excel appliqué à un modèle SIR dont une des équations a été rectifiée ? (voir https://www.lajauneetlarouge.com/covid-19-interrogations-sur-le-modele-epidemiologique-prise-en-compte-de-la-vaccination-et-du-variant-anglais/ )
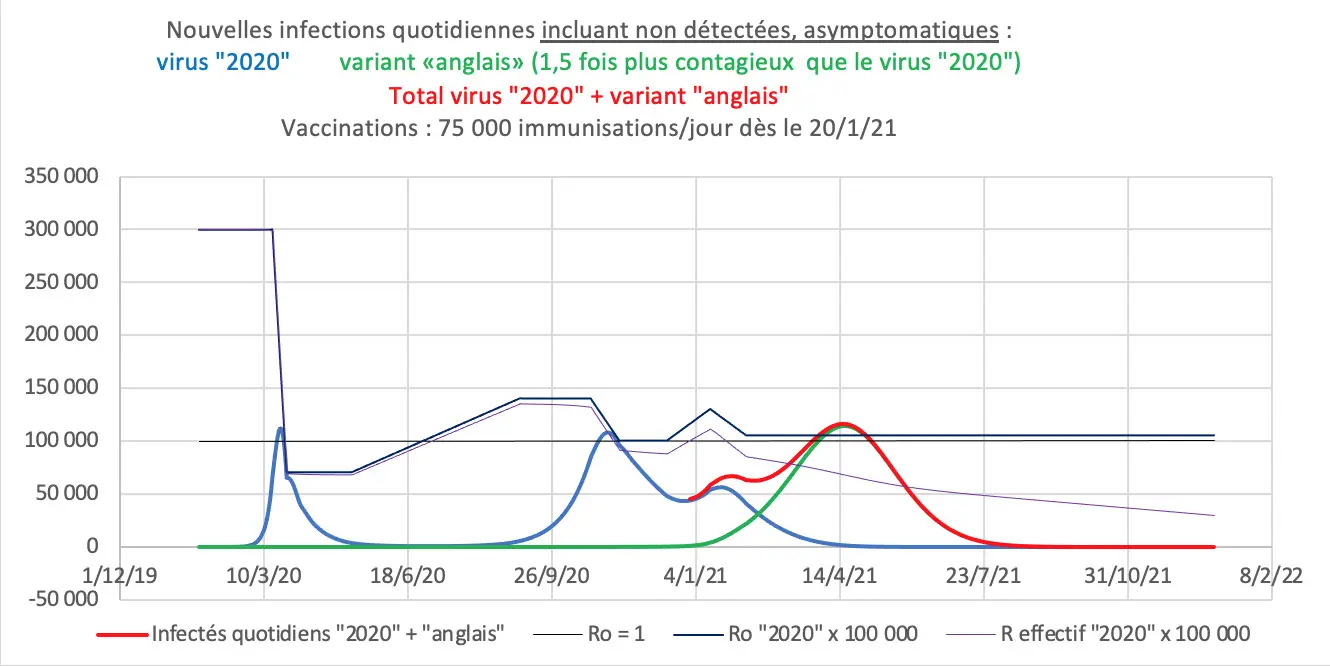
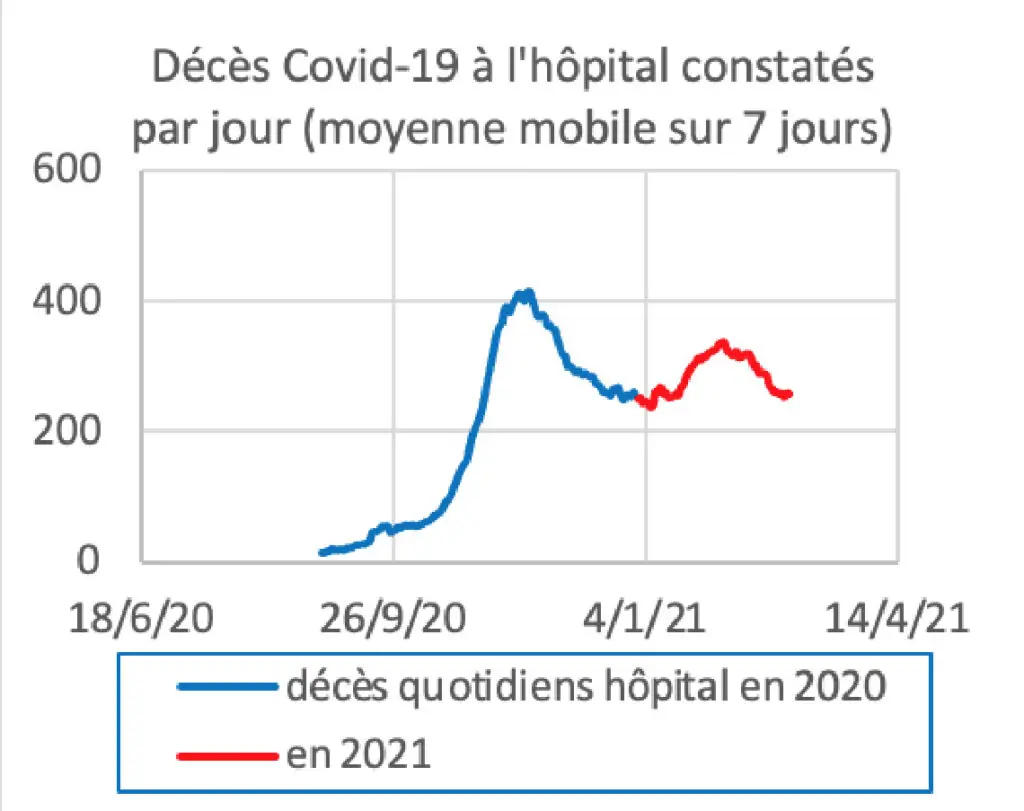
A comparer avec la courbe des décès constatés à l’hôpital qui est décalée d’une quinzaine de jours par rapport à la courbe des infections (courbe bleue en 2020, puis courbe rouge en 2021 à partir de la montée des infections dues au variant « anglais »).
Si aucune nouvelle mesure n’est prise, le maintien des R0 des virus « 2020 » et « anglais » à leurs niveaux actuels (R0 « 2020 » = 1,05 et R0 « anglais » = 1,57) va conduire en mars-avril à une 3ème vague présentant un nombre maximum quotidien d’infections sensiblement égal à celui des 2 vagues précédentes, mais pendant une durée plus longue (car l’ascension de chacune des vagues précédentes a été arrêtée par un confinement).
Pour tenter de réduire l’impact de cette 3e vague, deux possibilités théoriques dont nous allons comparer l’efficacité :
- augmentation très significative du rythme des vaccinations (passant de 75 000 immunisations/jour à 150 000 immunisations/jour à partir du 15 mars)
- diminutions modérées (2 hypothèses : – 5% et – 10%) des R0 du virus « 2020 » et de son variant « anglais » grâce à des mesures ayant une influence sur le comportement de la population. D’après notre modèle la proportion de la population S susceptible d’être infectée (car ni vaccinée, ni immunisée suite à une guérison, et ne bénéficiant pas d’une éventuelle immunité naturelle) notée habituellement S/N – N étant la population totale – est égale en début d’année 2021 à environ 0,86.
Les Reffectif correspondants sont alors 1,05 x 0,86 = 0,9 pour le virus « 2020 » et 1,57 x 0,86 = 1,35 pour le virus anglais. En début d’année 2021, l’infection due au virus « 2020 » est donc en train de régresser, tandis que l’infection due au variant « anglais » va croître jusqu’ à ce que S/N passe en-dessous de 1⁄1,57 = 0,64.
Bien noter que pour l’instant la part la plus importante de la différence entre S et N ne provient pas encore des vaccinations, dont l’effet n’a commencé à se faire sentir que fin janvier 2021, mais de l’immunisation acquise suite à des infections (auxquelles s’ajoutent d’éventuelles immunités naturelles).
Le point important est de déterminer l’évolution cumulée des deux types de virus dans différentes hypothèses.
Effet d’une accélération des vaccinations
Passage à 150 000 immunisations par jour à partir du 15 mars 2021
R0 « 2020 » stable à 1,05 à partir du 15/2/2021
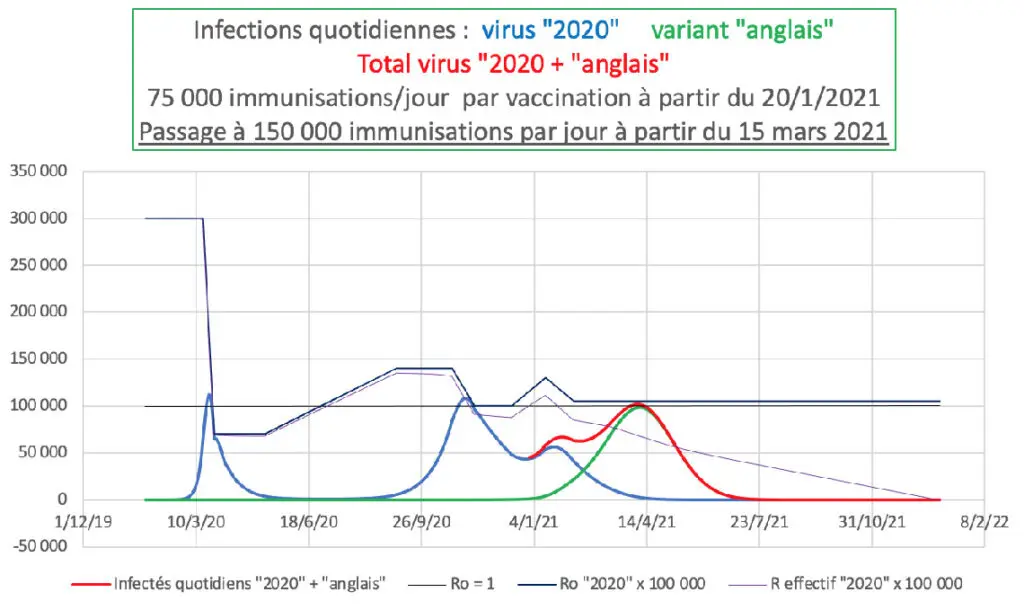
De toute évidence, une augmentation réaliste du rythme de vaccination n’est pas en mesure de réduire à elle seule et de façon satisfaisante l’ampleur de cette 3e vague.
Néanmoins, la vaccination prioritaire des plus fragiles aura un effet bénéfique rapide sur les évolutions de la charge des hôpitaux et de la létalité moyenne.
Effet d’un durcissement des mesures modifiant le comportement de la population
Réduction de 5 % des R0 (« 2020 » et « anglais ») à partir du 1er mars
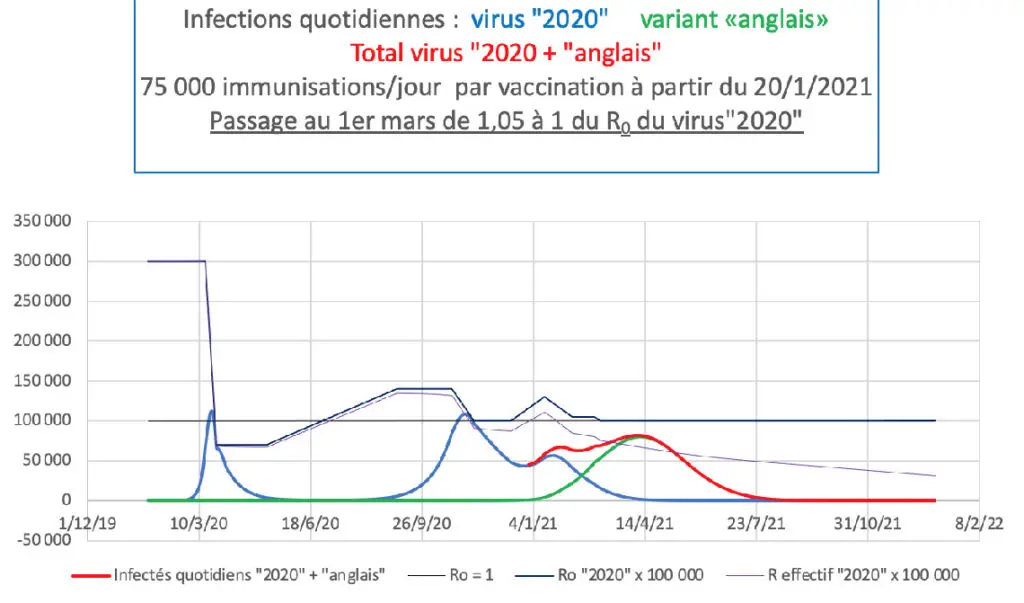
A court terme, cette diminution de 5% des R0 des deux types de virus a un effet plus important que le doublement des immunisations de 75 000 à 150 000 par jour au 15 mars.
Effet d’un durcissement des mesures modifiant le comportement de la population
Réduction de 10 % des R0 (« 2020 » et « anglais ») à partir du 1er mars
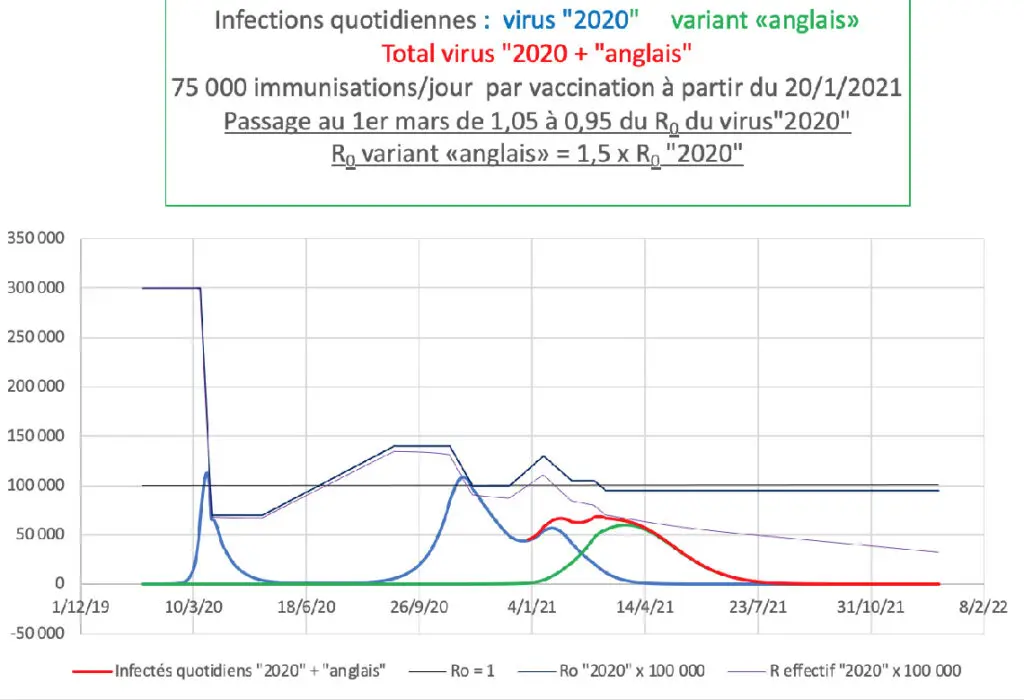
Effet accentué lorsqu’on passe à une diminution de 10% des R0 des deux types de virus.
Sensibilité des résultats à la contagiosité exacte du variant « anglais »
En fait, la contagiosité exacte du variant « anglais » est mal connue. Si on remonte à la source de l’information donnée par la plupart des médias, c’est-à-dire la note de Nicholas G. Davies (Centre for Mathematical Modelling of Infectious Diseases, London School of Hygiene and Tropical Medicine de Londres)
https://www.medrxiv.org/content/10.1101/2020.12.24.20248822v2
on y lit : « we estimate that VOC 202012⁄01 is 43–82% more transmissible than pre‑existing variants of SARS-CoV‑2 »
En comparant la courbe des décès à l’hôpital donnée plus haut à celles fournies par notre modèle (SIR rectifié) pour différentes valeurs de contagiosité, la meilleure estimation semble être une augmentation de 50% par rapport à celle du virus « 2020 ».
Les 3 diagrammes qui suivent montrent combien l’évolution de l’épidémie est sensible à la valeur exacte de l’augmentation de contagiosité due au remplacement du virus « 2020 » par son variant « anglais ».
Rappel de l’évolution avec un variant de contagiosité de + 50% par rapport au virus « 2020 »
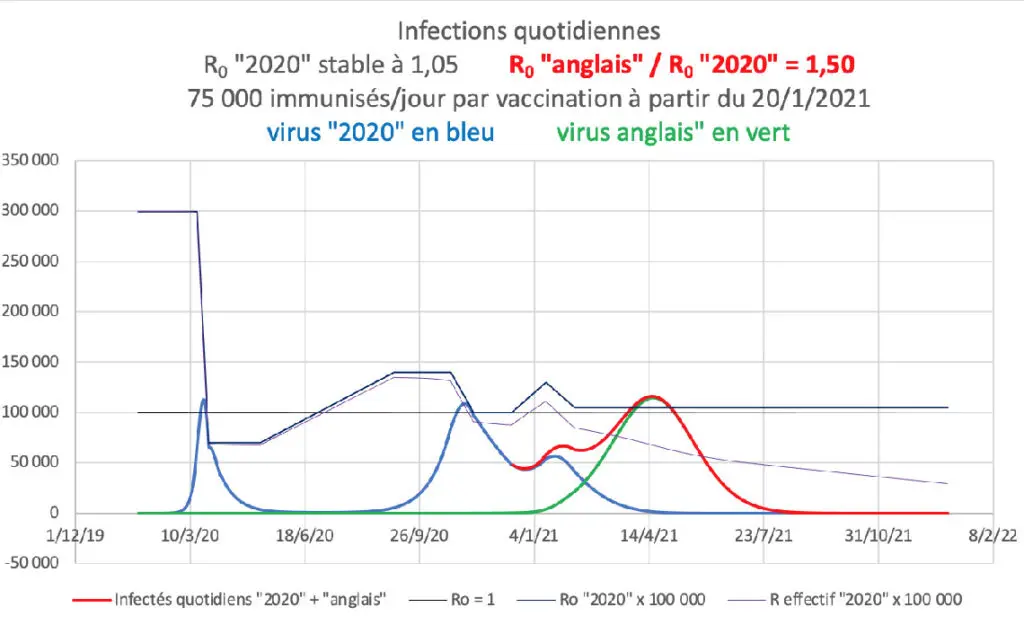
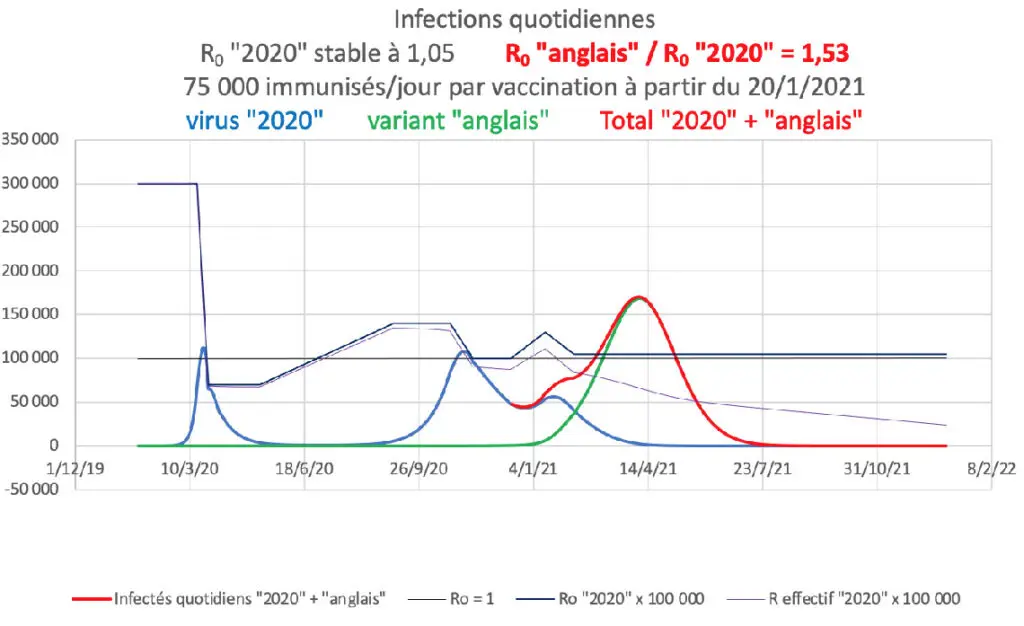
Le passage de 50% à 53% de la contagiosité additionnelle du variant « anglais » par rapport au virus « 2020 » fait croître de près de 50% le nombre quotidien maximum d’infections prévisibles en avril.
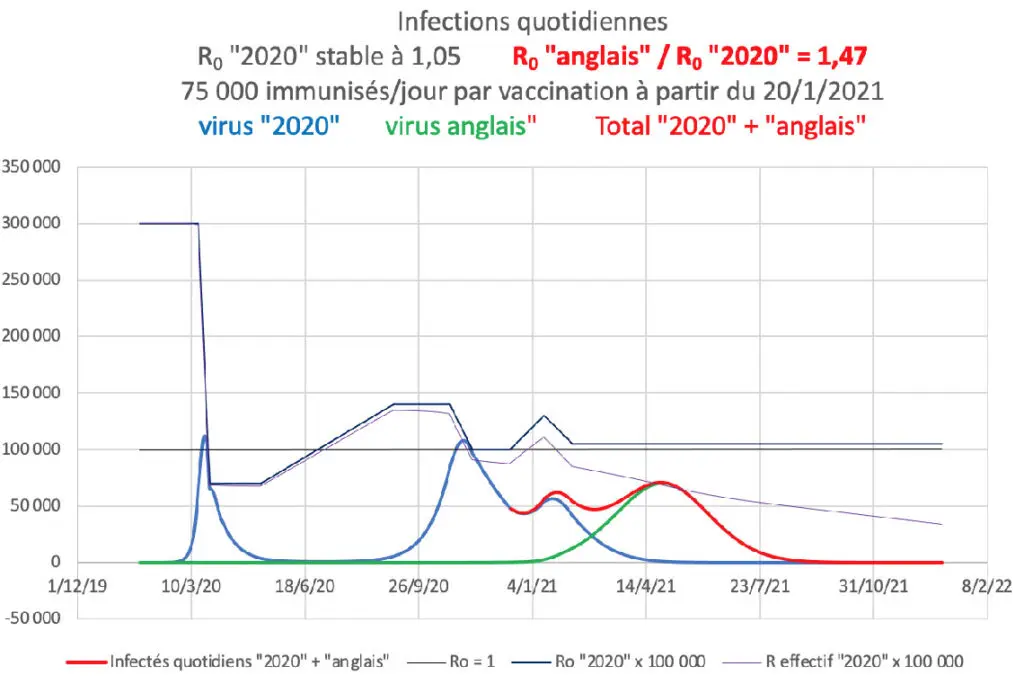
Le passage de 50% à 47% de la contagiosité additionnelle du variant « anglais » par rapport au virus « 2020 » réduit de près de 40% le nombre quotidien maximum d’infections prévisibles en avril.
Conclusions
NOMBRE DE NOUVELLES INFECTIONS QUOTIDIENNES : PIC D’AVRIL 2021
(infections non détectées – dont asymptomatiques – comprises)
|
R0 « 2020 » à partir du 15/2/2021 |
R0 variant « anglais » à partir du 15/2/2021 | Vaccinations : nombre d’immunisations par jour à partir du 20/1/2021 | Nombre quotidien maximum d’infections |
|
1,05 |
1,05 x 1,5 = 1,57 |
75 000 |
115 000 |
|
1,05 |
1,05 x 1,5 = 1,57 |
75 000 |
105 000 |
|
1 |
1,5 |
75 000 |
81 000 |
|
0,95 |
0,95 x 1,5 = 1,42 |
75 000 |
70 000 |
|
1,05 |
1,05 x 1,47 = 1,54 |
75 000 |
67 000 |
| 1,05 | 1,05 x 1,53 = 1,61 | 75 000 |
170 000 |
Pour réduire l’amplitude prévisible de la vague de mars-avril, des mesures modifiant le comportement de la population et destinées à faire baisser de 5 à 10% les R0 des 2 types de virus seront plus efficaces qu’une forte augmentation du rythme des vaccinations (telles qu’un doublement du nombre quotidien des immunisés à partir du 15 mars).
A aussi court terme, la contribution d’un accroissement du rythme de vaccination à une modération de la vague attendue en mars avril ne peut être que modeste. Néanmoins, la vaccination prioritaire des plus fragiles aura un effet bénéfique rapide sur les évolutions de la charge des hôpitaux et de la létalité moyenne.
A moyen terme cette vaccination jouera un rôle majeur dans la diminution progressive de la population susceptible d’être contaminée, donc de Reffectif (courbe violette).
Une extrême attention devra être apportée à la connaissance précise du supplément de contagiosité du variant « anglais » (ou d’autres variants !) par rapport au virus « 2020 » : s’il dépasse 50%, un confinement « dur » paraît inévitable.
Articles similaires :
Covid-19 : interrogations sur le modèle épidémiologique, Prise en compte de la vaccination et du « variant anglais »
La modélisation des épidémies à l’épreuve de la Covid-19
« Deuxième vague » Covid-19 : perspectives 2020–2021
La précaution, pas le principe !
Covid-19 : perspectives d’infection par le variant Omicron
3 Commentaires
Ajouter un commentaire
merci de cet article formatif quoique un peu technique . Quels sont les logiciels utilisé pour prévisions / et comment dans une interview sur you tube le directeur de l’OMS à Geneve au début de la pandémie pouvait il chiffrer les pertes à 30 millions ? / pensez vous que nous aurons une quatrieme vague malgré un bon taux de vaccination cet Automne ?
suite à commentaire cf ” the concept of Ro in epidemiology ” article dans journal of the Royal Society .CQFD
Pour une population N considérée comme homogène, il y a vague dès que Ro x S / N est supérieur à 1, S étant la population susceptible d’être infectée (donc n’ayant pas été vaccinée, n’étant pas immunisée suite à une infection et ne bénéficiant pas d’une éventuelle immunité naturelle).
Ro dépend du virus et des variables comportementales de la population. Avec les virus « 2020 » Ro = 3 dans les conditions de vie françaises avant février 2020, environ 1 avec les conditions actuelles (confinement modéré, mesures-barrières). Avec le virus « anglais » on passe à Ro = 4,5 dans les conditions de vie françaises avant février 2020 et environ 1,5 avec les conditions actuelles. Début 2021 (avant début des vaccinations), vraisemblablement entre 10% et 15% de la population était immunisée. Donc, avec le seul virus « 2020 », maintenir Ro un peu au-dessus de 1 devait suffire à faire régresser l’épidémie, la vaccination permettant ensuite de laisser remonter lentement ce Ro jusqu’à celui du « monde d’avant » (3).
Le variant « anglais » a déjoué ces calculs. Il est en train de remplacer totalement le virus « 2020 » et impose donc de faire passer rapidement S/N en dessous de 1⁄1,5 = 0,67 grâce aux effets combinés de la vaccination et d’un reconfinement. Une fois passé le risque de 3ème vague en avril, le problème sera de laisser remonter le So du variant anglais (ou d’un autre variant encore plus contagieux !) pour retrouver les conditions de vie de 2019 !
Enfin il faut bien voir qu’atteindre l’immunité collective ne signifie pas que l’épidémie est terminée : elle commence simplement à régresser. Je vous donne les ordres de grandeur : avec un Ro de 3 on atteint théoriquement l’immunité collective quand 67% de la population a été contaminée ou vaccinée, mais pour la fin de l’épidémie il faut atteindre un taux de 94%, la formule permettant le calcul théorique (facile par itération avec Excel) étant : Taux = 1 – exp( – Ro x Taux). Pour un Ro de 4,5 la quasi-totalité de la population aura été ou contaminée ou vaccinée.
Au début de l’épidémie on estimait la létalité à un peu plus de 0,5%. Sans vaccination ni aucune modification du comportement de la population mondiale (donc Ro = 3), on pouvait estimer que 94% de la population mondiale serait infectée ce qui correspond bien à environ 30 millions de décès. Mais ceci ne tenait pas compte du fait que Ro = 3 correspond à un mode de vie occidental (frénésie de contacts, de circulation des individus …), des diverses mesures de confinement, de quarantaine, de port de masques, de l’âge moyen dans les différentes parties du monde … D’autre part, même en absence de consignes gouvernementales, les populations évitent spontanément les contacts avec les malades ! (voir mon article d’octobre 2020).
Enfin les modèles. Au départ tous sont basés sur celui de 1927 (communication de Kermack et McKendrick à la Royal Society de Londres). Au départ ceux-ci ont écrit des équations permettant de tout rendre variable en fonction du temps. En l’absence d’ordinateurs, ces équations étaient inexploitables. Ils ont donc défini un « special case » utilisable qui contenait une option de simplification malheureuse (probabilité de guérison uniforme, ne dépendant pas du temps depuis lequel un individu était contaminé, alors que c’est la durée de la maladie qui est assez uniforme). Leurs successeurs ont « oublié » la partie complexe de la communication de 1927 et pris pour argent comptant (et présenté comme tel aux étudiants en épidémiologie) le « special case » erroné. Comme celui-ci donnait des résultats incompatibles avec la réalité (il est insuffisamment réactif aux variations dans le temps du nombre d’infectés, à la hausse comme à la baisse) les mathématiciens ne voulant pas donner l’impression qu’ils touchaient aux sacro-saintes équations de 1927 se sont lancés dans l’élaboration de modèles d’une grande complexité dont une partie ne servait qu’à corriger le caractère erroné de ces équations, action camouflée car noyée dans d’autres développements destinés à affiner le modèle. Le résultats est une floraison de modèles, chacun établi avec des recettes mathématiques « maison », généralement mal documentés et dont les codes informatiques ne sont pas rendus publics (voir en particulier les justifications données par N. Ferguson, considéré comme le meilleur spécialiste de ce domaine : « En mars, Ferguson a admis que son modèle de la maladie Covid-19 de l’Imperial College était basé sur un code informatique vieux de 13 ans, non documenté, destiné à être utilisé pour une pandémie de grippe redoutée, plutôt que pour un coronavirus. Ferguson a refusé de divulguer son code original pour que d’autres scientifiques puissent vérifier ses résultats. Il n’a publié une série de codes fortement révisés que la semaine dernière, après un délai de six semaines).
C’est la raison pour laquelle je préconise d’utiliser, au moins de façon complémentaire, un modèle simplifié corrigeant le « special case » de 1927 (ce qui est très facile, voir mes articles) et utilisant Excel, afin que des non-mathématiciens (en particulier les énarques et les médecins qui co-gèrent actuellement les actions des pouvoirs publics) puissent mieux comprendre l’évolution de l’épidémie et demander éventuellement aux responsables des modèles institutionnels des vérifications ou les résultats d’hypothèses différentes.