Covid-19 : Enseignements et crédibilité des modèles épidémiologiques

Covid-19 : Enseignements et crédibilité des modèles épidémiologiques. Essayer d’y voir clair grâce à un mini-modèle graphique interactif basé sur un simple tableur et n’utilisant que les mathématiques enseignées à l’école primaire.
Rappel du modèle fondateur de 1927
La modélisation moderne des épidémies remonte à une communication faite en 1927 à la Royal Society de Londres par les Écossais Kermack (biochimiste) et McKendrick (médecin militaire).
Cette communication, dont dérivent la plupart des modèles actuels, est en fait une variante du traditionnel problème de réservoir et de robinet de l’ex Certificat d’études primaires. La population est répartie en 3 réservoirs (dits compartiments SIR) : les Sains (susceptibles d’être infectés), les Infectés (malades pouvant contaminer des personnes saines) et les Rétablis (ne pouvant plus contaminer personne, car guéris et immunisés, ou décédés).
Les équations du modèle de 1927 définissent les débits dynamiques entrant (robinet) et sortant (bonde) dans le réservoir/compartiment des Infectés, leur sortie tenant compte du débit d’entrée et de la durée de la période d’infection (dans ce modèle simple, on considère que les durées d’infection et de contagiosité coïncident).
Au début de leur communication (page 702), Kermack et McKendrick ont envisagé un modèle où tous les paramètres, dont les taux de contamination φ(t) et de sortie d’infection ψ(t) pouvaient varier au cours de l’épidémie. Mais comme en 1927 n’existaient ni ordinateurs ni solveurs informatiques, ils ont défini des versions simplifiées (« Special cases », voir page 709) des équations générales, vraisemblablement dans l’espoir (vain) de pouvoir trouver une manière d’exprimer S, I et R sous forme de fonctions analytiques du temps.
Le deuxième « Special case » (page 712) dit « Constant rates » suppose que les taux d’infections φ et de « removal » (guérisons et décès) ψ sont constants, ce qui conduit à la forme classique figurant depuis 1927 dans tous les cours d’épidémiologie :

Ces équations sont à la base de la plupart des multiples systèmes de simulation d’épidémies proposés depuis cette époque, avec des notations qui sont habituellement :
dS / dt = – β S I nouvelles infections
dI / dt = β S I – γ I
dR / dt = γ I guérisons ou décès
γ est l’inverse de la durée moyenne d’infection D supposée relativement uniforme
L’erreur provenant de l’expression γ I
La dernière équation est tout à fait inexacte dans le cas d’une hausse ou d’une baisse rapide du nombre d’infectés I.
En cas de hausse de I, les personnes qui guérissent (ou meurent) à l’instant t sont celles qui sont tombées malades à l’instant (t‑D). Dire que le rythme de ces guérisons est égal à γ I revient à le surestimer en le calculant non pas à partir de la population infectée à l’instant (t‑D), mais à partir de celle qui a été infectée de façon croissante entre (t‑D) et t. Ceci conduit donc à sous-estimer le nombre d’infectés et donc le nombre de nouvelles infections qui lui est proportionnel d’après la 1ère équation.
Inversement, en cas de baisse de I, l’utilisation de γ I revient à sous-estimer le rythme des guérisons en le calculant à partir de la population qui a été infectée de façon décroissante entre (t‑D) et t, ce qui conduit à surestimer le nombre d’infectés et donc le nombre de nouvelles infections.
L’équation à « Constant rates » « étouffe » donc par effet tampon les variations rapides du nombre de personnes infectées et de nouvelles infections, à la hausse (début de l’épidémie, déconfinement) comme à la baisse (confinement).
Curieuses dérives mathématiques
Un mystèrePourquoi les modélisateurs épidémiologiques réputés sérieux ont-ils préféré conserver (et enseigner sans mise en garde dans leurs cours aux étudiants) l’équation erronée de 1927, tout en utilisant dans leurs modèles des procédés divers, propres à chacun d’entre eux, pour en corriger les défauts ? Il semble qu’aurait été plus simple de remplacer l’équation dR / dt = γ I par dR / dt = – dS(t ‑ D) /dt où D = 1/ γ |
Quand les mathématiciens qui cherchaient à simuler l’évolution des épidémies ont réalisé que les résultats de modèles basés sur les « Constant rates » de 1927 ne correspondaient pas à la réalité, ils n’ont pas voulu remettre en cause de façon visible l’équation erronée de 1927. Plutôt que de remplacer cette dernière par une équation presqu’aussi simple, mais adaptée aux contextes dynamiques (voir encadré plus haut), ils ont préféré donner l’illusion qu’ils conservaient l’équation de 1927 comme base de leurs modèles, tout en introduisant dans ces derniers diverses corrections mathématiques plus ou moins complexes. On peut citer par exemple le passage à des modèles stochastiques ou à ce que Cédric Villani a qualifié de « discrétisation du modèle, de façon à pouvoir incorporer un effet mémoire » dans sa note sur la modélisation épidémiologique remise le 30 avril 2020 à l’Office parlementaire d’évaluation des choix scientifiques et technologiques qu’il préside actuellement.
Modèles stochastiques
Ayant constaté que l’utilisation des équations différentielles du « Constant rates » conduisait à un démarrage trop lent d’une épidémie simulée à partir de l’arrivée d’un unique infecté (le « patient 0 ») certains mathématiciens ont estimé qu’il était indispensable de passer à de complexes modèles probabilistes. Voir par exemple « Modéliser la propagation d’une épidémie » d’Hugo Falconet et Antoine Jego https://docplayer.fr/56627577-Modeliser-la-propagation-d-une-epidemie.html qui contient de nombreuses pages de calcul basées sur des chaînes de Markov, choix quelque peu étrange puisqu’il reproduit à chaque étape l’ « erreur de 1927 » (probabilité de guérison ne dépendant pas de l’ « âge » de l’infection).
Discrétisation du modèle
Voici le commentaire qu’a déposé après l’article https://www.lajauneetlarouge.com/modeles-mathematiques-depidemies-les-plus-elabores-pourquoi-leurs-previsions-initiales-sont-elles-souvent-excessivement-pessimistes/ un membre du CNRS (qui n’est pas spécialiste du domaine, mais a visiblement été bien renseigné par ses collègues qui le sont).
» Malgré ce que vous semblez penser les modélisateurs professionnels connaissent évidemment ce que vous appelez l’erreur de 1927, et savent quand elle est gênante ou pas, selon ce que l’on veut faire. S’il le faut ils l’éliminent. On peut le faire de différentes façons. Par exemple en la multipliant, si je puis dire : supposons qu’on veut décrire la cinétique du passage I–>R d’un modèle SIR.
La version basique du modèle donne dI/dt=-I/D et dR/dt=I/D, soit une décroissance de type exponentielle de I (avec une probabilité de guérison indépendante de la date d’infection, comme vous le dites). Maintenant introduisez n stades intermédiaires entre I et R, appelons les J1, J2 etc, et écrivez : dI/dt=-I/D, dJ1/dt=I/D‑J1/D’, dJ2/dt=J1/D’-J2/D’ etc … jusqu’à dR/dt=Jn/D’. Ce faisant vous introduisez un retard à la guérison. L’effectif total des personnes infectées (la somme de I et de tous les Jn) ne décroit plus exponentiellement, mais selon une fonction de type sigmoïde, avec une période pendant laquelle il ne se passe pas grand‑chose, suivie d’une décroissance concentrée autour d’une durée bien déterminée depuis la date de contamination. De cette façon on génère très facilement une distribution de type loi gamma pour la probabilité de guérison en fonction du temps écoulé depuis la contamination (on peut jouer sur n et D’).Je ne suis pas l’inventeur de cette astuce numérique, elle fait partie de celles couramment utilisée par les modélisateurs.… Ils n’en restent évidemment pas à la version de 1927 du modèle ! »
On peut légitimement se demander si ces corrections plus ou moins occultes à une insuffisante réactivité de modèles basés sur les équations à « Constant rates » sont efficaces quand on réalise que les prévisions des modélisateurs ont généralement sous-estimé la vigueur de la 2ème vague de septembre-octobre 2020 ainsi que la rapidité de la réaction au confinement de la fin octobre 2020 qui a fait que la prévision présidentielle de 9 000 personnes en réanimation au 15 novembre « quoi qu’on fasse » a été démentie par les faits.
Ne pas faire d’amalgame entre complexification légitime du modèle SIR et complexification destinée à compenser l’erreur du SIR à « Constant rates » de 1927
Bien entendu il existe une forme de complexification tout à fait légitime du modèle SIR de base, mais celle-ci ne devrait venir qu’après une rectification préalable de l’« erreur de 1927 » et ne pas servir de camouflage à l’absence de cette rectification, potentielle cause d’erreurs importantes.
Une forme de complexification « saine » consiste par exemple à tenir compte du fait que les individus n’ont pas une contagiosité homogène, que les interactions entre individus peuvent dépendre de multiples facteurs (âge, type d’habitat, d’activité, …)
Exemple d’un modèle compensant de façon claire l’erreur du SIR à « Constant rates » de 1927
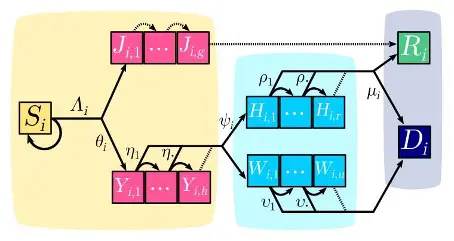
| COVID-19 epidemic discrete time model structure. Each square represents a group of individuals who share the same clinical kinetics and who contribute equally to the epidemic dynamics. Contiguous squares form a compartment, in which each individual progresses day after day, therefore allowing to capture memory effects of the infection age Schéma extrait de ⟨hal-02619546⟩ Mircea Sofonea, Bastien Reyné, Baptiste Elie, Ramsès Djidjou-Demasse, Christian Selinger, et al.. Epidemiological monitoring and control perspectives : application of a parsimonious modelling framework to the COVID-19 dynamics in France. |
Réactions opposées des universitaires mathématiciens et physiciens et des universitaires du milieu médical
Lorsqu’on leur présente ce qui précède, les universitaires mathématiciens et physiciens rompus aux techniques de simulation estiment généralement que ne serait que du replâtrage toute approche qui ne remplacerait pas l’équation erronée de 1927 par une équation adaptée à la modélisation d’un phénomène dynamique.
L’approche du monde médical est radicalement différente. En général, ses membres (même « infectiologues ») fuient tout débat sur ce sujet, en arguant du fait que la simulation épidémiologique est un secteur extrêmement spécialisé, qui fait appel à des notions mathématiques de très haut niveau. Les seules personnes qualifiées pour répondre à une telle remise en cause seraient les rares modélisateurs de grands organismes auxquels ils font confiance.
Conséquences sur les prises de décisions des pouvoirs publics
Les pouvoirs publics sont donc entretenus par le milieu médical dans l’idée que la modélisation épidémiologique est une activité extrêmement complexe, faisant appel à des notions mathématiques de très haut niveau, que ne maîtrise généralement pas la quasi-totalité du personnel administratif et politique qui prend finalement les grandes décisions.
Sont donc présentés aux décideurs les résultats de « boîtes noires » provenant de différentes équipes, dont les codes informatiques ne sont pas rendus publics. Seuls sont accessibles des rapports dont un exemple-type datant du 23 février 2021 :
« A race between SARS-CoV‑2 variants and vaccination : the case of the B.1.1.7 variant in France » par Paolo Bosetti, Cécile Tran Kiem, Alessio Andronico, Juliette Paireau, Daniel Levy Bruhl, et al. https://hal.archives-ouvertes.fr/pasteur-03149525
qui contient l’examen d’un nombre limité d’hypothèses, mais ne permet pas à des non‑spécialistes de modifier eux-mêmes de façon fine des hypothèses telles que le rythme des vaccinations, la date à laquelle sont mises en œuvre des mesures de couvre-feu, de confinement, de déconfinement, etc …
Intérêt d’un mini-modèle graphique interactif basé la correction de l’erreur du « Constant rates » de 1927 et l’utilisation d’un tableur
Pour comprendre les perspectives d’évolution à court terme d’une épidémie il serait intéressant d’évaluer les résultats donnés par l’utilisation d’un tableur après correction de la simplification erronée du « Constant rates » de 1927 (voir plus haut la méthode proposée dans l’encadré « Un mystère »).
Un tableur de type Excel présente l’avantage d’être connu d’une population beaucoup plus large qu’un solveur connu des seuls mathématiciens. Son emploi pour simuler une épidémie est expliqué dans l’annexe de l’article https://www.lajauneetlarouge.com/covid-19-une-modelisation-simple-utilisant-excel-accessible-aux-non-mathematiciens-et-pleine-denseignements/
Voici ce que donne l’exploitation d’un tel tableur après introduction de paramètres connus ou vraisemblables à la date du 6 avril 2021.
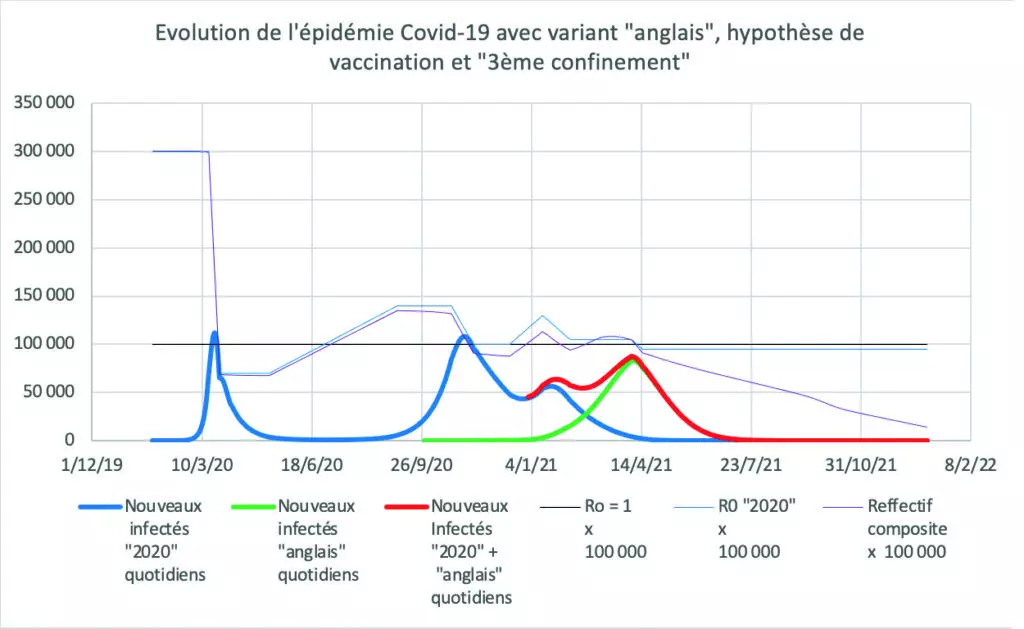
Attention, les nombres de nouveaux infectés annoncés quotidiennement par les pouvoirs publics ne sont pas les nombres réels, mais ceux des seuls nouveaux infectés détectés par des tests. Ils dépendent donc entièrement de la politique de tests. On estime généralement que début 2021 le nombre quotidien réel de nouveaux infectés (dont les asymptomatiques) était le double du nombre de nouveaux infectés annoncé.
| Une version interactive téléchargeable permet au lecteur de voir l’effet de différentes hypothèses qu’il peut introduire lui-même dans le tableur :
- supplément de contagiosité du variant « anglais » par rapport au virus « 2020 » : case W24 - R0 correspondant au virus « 2020 » et au comportement de la population : colonne W à partir du 1er avril 2021 - nombre quotidien de personnes immunisées par vaccination : colonne Q |
Hypothèses (modifiables) du tableur téléchargé :
- supplément de contagiosité du variant « anglais » de 48% par rapport au virus « 2020 ». (soit un R0 très élevé de 4,44 dans les conditions de vie du « monde d’avant »)
- 75% des vaccinés sont immunisés 10 jours après la 1ère injection. Il a été tenu compte du nombre réel d’injections en janvier, février et mars (moyenne journalière établie à partir du total mensuel). Le nombre de mars a été reconduit dans le tableur jusqu’à la fin de l’année. Bien entendu, le nombre quotidien d’immunisations à partir d’avril devra être mis à jour
- le R0 du virus de type « 2020 » suit le mieux possible jusqu’à fin mars l’épidémie réelle, en tenant compte des mesures gouvernementales (confinements, couvre-feux, déconfinements, port de masques, …). Pour mémoire ce R0 était d’environ 3 jusqu’au 1er confinement, pendant lequel il est passé environ à 0,7. Depuis il se promène entre 0,9 et 1,5






