Covid-19 : une modélisation simple utilisant Excel, accessible aux non-mathématiciens et pleine d’enseignements

Les équa­tions dif­féren­tielles établies par Ker­ma­ck et McK­endrick en 1927 per­me­t­tent de mod­élis­er le développe­ment d’une épidémie. Mal­gré leur sim­plic­ité, elles n’ont pas de solu­tion pou­vant être exprimée sous forme ana­ly­tique. Quant aux mul­ti­ples mod­èles dérivés, de plus en plus com­plex­es sur le plan math­é­ma­tique, leurs prévi­sions n’ont pas tou­jours été fiables. Or l’emploi d’Excel n’est pra­tique­ment jamais évo­qué dans les cours d’épidémiologie, alors qu’il per­met de ren­dre la mod­éli­sa­tion d’une épidémie com­préhen­si­ble à des non-math­é­mati­ciens, de leur de mon­tr­er sa per­ti­nence et de leur faire com­pren­dre quelles sont les futures évo­lu­tions possibles.

Pour le non-math­é­mati­cien, tir­er per­son­nelle­ment des enseigne­ments pra­tiques du mod­èle épidémi­ologique de Ker­ma­ck et McK­endrick, même sous sa forme la plus sim­ple dite SIR, paraît très ardu : les spé­cial­istes lui par­lent d’exponentielles, de dérivées, d’équations dif­féren­tielles non linéaires impos­si­bles à résoudre sans recourir à des solveurs infor­ma­tiques. Le résul­tat est une prise de dis­tance fréquente vis-à-vis de cette dis­ci­pline de la part de beau­coup de médecins, qui va pour cer­tains jusqu’à l’affirmation qu’elle n’est pas plus crédi­ble que l’astrologie.

Le modèle SIR 

Rap­pelons que dans ce mod­èle la pop­u­la­tion com­posée de N indi­vidus est divisée en 3 « compartiments » :

• S pop­u­la­tion saine non contaminée ;
• I pop­u­la­tion infec­tée réputée contagieuse ;
• R pop­u­la­tion « remise » c’est-à-dire guérie et réputée immu­nisée, ou décédée.

Exprimées en lan­gage de non-math­é­mati­ciens util­isa­teurs d’Excel, les équa­tions de Ker­ma­ck et McK­endrick sig­ni­fient que :

• La pop­u­la­tion S (au départ égale à N moins quelques indi­vidus infec­tés) dimin­ue quo­ti­di­en­nement de β.S.I indi­vidus (β est égal à R₀ /(N.D), R₀ étant le « taux de repro­duc­tion ini­tial » sou­vent évo­qué par les médias et D la durée moyenne pondérée en jours d’infection avant guéri­son ou décès).

Bien not­er que la nota­tion tra­di­tion­nelle R₀ n’a rien à voir avec R à l’instant 0.

• La pop­u­la­tion R (au départ nulle) aug­mente quo­ti­di­en­nement de γ.I indi­vidus (γ étant l’inverse de D).
• La pop­u­la­tion I (au départ quelques indi­vidus) est la dif­férence entre N et (S + R).

Nota : paraî­trait plus logique une mod­éli­sa­tion où, au lieu de γ.I indi­vidus entrant le jour J dans le com­par­ti­ment R, y bas­culeraient ceux qui ont quit­té le jour (J‑D) le com­par­ti­ment S. Néan­moins les équa­tions clas­siques de Ker­ma­ck et McK­endrick présen­tent l’avantage d’avoir fait depuis 1927 l’objet de nom­breuses études qui ont fourni un cer­tain nom­bre de con­clu­sions validées par l’observation de cas con­crets d’épidémie. Une com­para­i­son entre des mod­éli­sa­tions Excel fondées sur les deux types d’équations n’a pas mon­tré de dif­férence affec­tant de façon fon­da­men­tale les résul­tats exposés dans cet arti­cle, qui est donc basé sur l’utilisation des équa­tions traditionnelles. 

Où Excel excelle

À par­tir de D, N et R₀ il est facile de bâtir un tableau Excel don­nant l’évolution de S, I et R et de leurs vari­a­tions quo­ti­di­ennes pen­dant quelques cen­taines de jours. L’avantage sur des méth­odes math­é­ma­tiques clas­siques est l’extrême sou­p­lesse avec laque­lle ce logi­ciel per­met d’introduire des don­nées d’entrée suiv­ant n’importe quelle évo­lu­tion au cours du temps, en par­ti­c­uli­er pour R₀ (et par voie de con­séquence β).

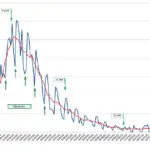
Le dia­gramme suiv­ant mon­tre l’évolution de I et de R au début d’une épidémie qui, dans le cadre de vie habituel d’un pays de 67 mil­lions d’habitants, présente un R₀ de 3. Le 17 mars le nom­bre de nou­veaux infec­tés quo­ti­di­ens atteint 100 000, ce qui risque d’entraîner 20 jours plus tard un nom­bre de décès quo­ti­di­en de 500 à 1 000, compte tenu d’une létal­ité réelle de 0,5 à 1 % (voir plus loin). Les pou­voirs publics décrè­tent alors un con­fine­ment général qui fait baiss­er immé­di­ate­ment R₀ à 0,7 pen­dant 55 jours. Après le décon­fine­ment du 11 mai, en par­ti­c­uli­er sous l’influence de mou­ve­ments lib­er­taires niant la per­sis­tance de l’épidémie, R₀ remonte pro­gres­sive­ment de façon linéaire jusqu’à 1,3 en 4 mois, puis se sta­bilise à ce niveau à par­tir de sep­tem­bre 2020.

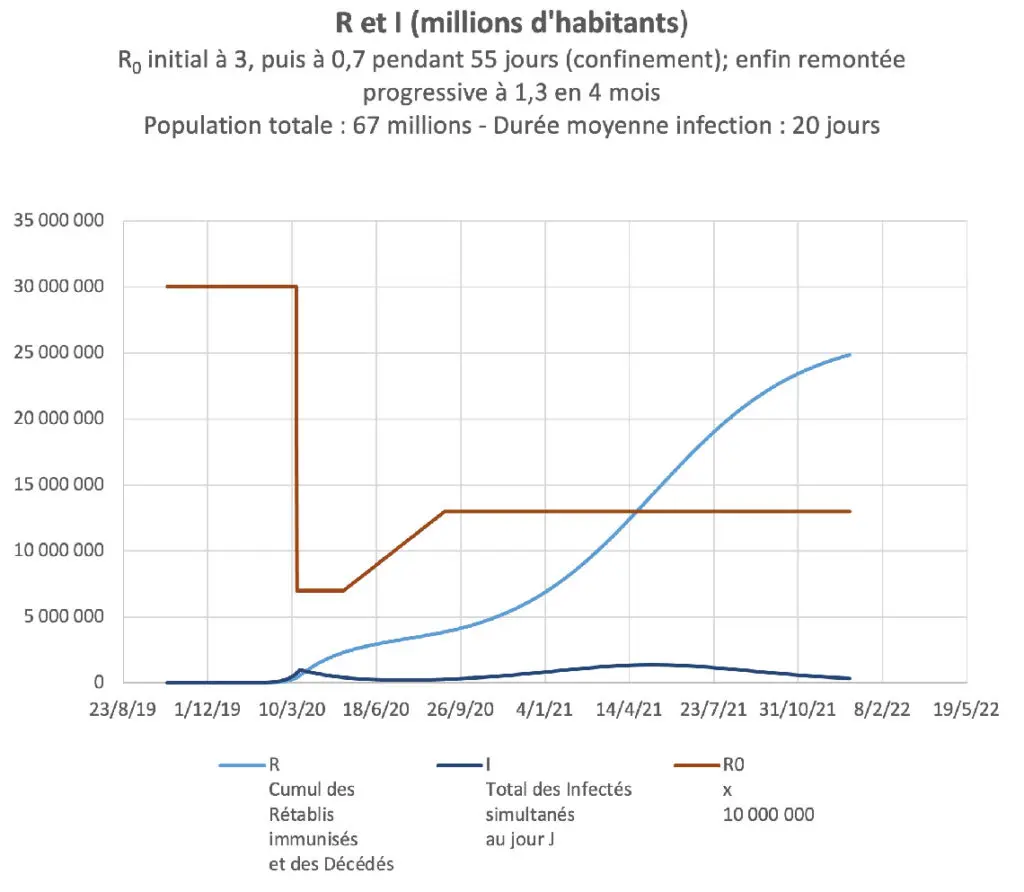
Le mod­èle SIR util­isant Excel mon­tre que le nom­bre d’infectés simul­tanés qui avait aug­men­té jusqu’au début du con­fine­ment (mars 2020) décroît jusqu’à la fin juil­let 2020. Ensuite, si le virus n’évolue pas, si R₀ reste sta­ble à 1,3 et si aucun nou­veau traite­ment effi­cace n’est mis en œuvre, le nom­bre d‘infectés simul­tanés croît jusqu’à un max­i­mum en juin 2021 (courbe bleu fon­cé) puis dimin­ue jusqu’à ce que l’immunité col­lec­tive cor­re­spon­dant à R₀ = 1,3 soit atteinte (env­i­ron 40 % de la pop­u­la­tion immu­nisée suite à guéri­son ou à toute autre cause, voir plus bas), ce qui ne survient qu’en 2022.

À la mi-août 2020, le cumul de per­son­nes qui ont été con­t­a­m­inées (courbe bleu clair) est d’environ 4 mil­lions. Une létal­ité réelle de 0,5 à 1 % con­duit à 20 à 40 000 décès depuis le début de la pandémie, fourchette com­pat­i­ble avec les chiffres observés en France.

Si les con­di­tions rap­pelées plus haut restent inchangées, l’évolution ultérieure prévue par Excel cor­re­spond ensuite à une hausse sen­si­ble entre le creux de juil­let 2020 et le print­emps 2021 du nom­bre quo­ti­di­en de nou­veaux infec­tés. Toute­fois cette hausse sera beau­coup moins rapi­de que celle de mars 2020 où le nom­bre de nou­veaux con­t­a­m­inés et de décès dou­blait chaque semaine. On assis­tera ensuite à une lente décrois­sance jusqu’à extinc­tion de l’épidémie début 2022 (à con­di­tion que R₀ reste à 1,3 !). Mais plusieurs élé­ments sont sus­cep­ti­bles de mod­i­fi­er cette prévi­sion : muta­tions imprévis­i­bles du virus, disponi­bil­ité de traite­ments des malades réduisant la durée d’infection, arrivée de vac­cins, sans oubli­er les réac­tions com­porte­men­tales de la pop­u­la­tion, que ce soit par prise de con­science et ini­tia­tives indi­vidu­elles (surtout chez les plus vul­nérables) ou par respect de con­signes indica­tives ou coerci­tives des pou­voirs publics.

Létalités réelle et apparente 

Le taux de létal­ité réel, ou infec­tion facil­i­ty rate (IFR), est le rap­port entre le nom­bre de décès imputés à l’épidémie et le nom­bre total de per­son­nes (y com­pris les asymp­to­ma­tiques) qui ont été infec­tées par le virus cor­re­spon­dant. Pour des raisons pra­tiques, ce dernier nom­bre ne peut être qu’estimé, car il n’est pas mesurable : pour un pays comme la France, à rai­son de 100 000 tests par jour, il faudrait près de deux ans pour tester une seule fois toute la population.

Cette létal­ité dépend de car­ac­téris­tiques du virus qui, dans le cas de la Covid-19, parais­sent jusqu’à main­tenant assez sta­bles et assez sem­blables dans l’ensemble des pays touchés. Des dif­férences entre pays et régions peu­vent appa­raître pour des raisons de fond (état de san­té général de la pop­u­la­tion, qual­ité du sys­tème de soins) et des méth­odes diver­gentes de saisie des motifs de décès, en par­ti­c­uli­er dans les cas fréquents de comor­bid­ité. Au moment où cet arti­cle est écrit, l’estimation du taux de létal­ité réel de cette infec­tion, au moins en France et dans des pays de niveau de développe­ment com­pa­ra­ble, sem­ble être une fourchette allant de 0,5 à 1 %.

Le taux de létal­ité appar­ent, ou case facil­i­ty rate (CFR), est le rap­port entre le nom­bre de décès imputés à l’épidémie et le nom­bre de per­son­nes qui ont été testées pos­i­tives. La létal­ité appar­ente est donc totale­ment dépen­dante de la poli­tique de tests qui varie énor­mé­ment de pays à pays (par exem­ple aux États-Unis, on a longtemps testé beau­coup plus qu’en France). Lorsqu’ils sont fondés sur des « létal­ités » tout court qui sont en fait des létal­ités appar­entes, les nom­breux arti­cles ou ouvrages qui pré­ten­dent com­par­er à par­tir de ce chiffre l’efficacité de dif­férents sys­tèmes de soins face à ce virus sont donc ineptes.

“La létalité n’a pas d’influence directe sur la propagation de l’épidémie.”

Dans un mod­èle épidémi­ologique, la létal­ité n’a pas d’influence directe sur la prop­a­ga­tion de l’épidémie, puisque ce qui déter­mine cette dernière est la baisse pro­gres­sive du nom­bre d’individus pou­vant être con­t­a­m­inés, que les autres aient été immu­nisés par infec­tion-guéri­son ou vac­ci­na­tion ou qu’ils n’aient pas survécu à l’infection.

Taux de contamination de la population apportant une immunité collective (herd immunity)

L’emploi d’Excel per­met de déter­min­er facile­ment le taux d’immunité col­lec­tive, c’est-à-dire le pour­cent­age de la pop­u­la­tion qui doit avoir été con­t­a­m­iné (ou vac­ciné) pour que l’épidémie s’arrête d’elle-même. Il suf­fit de pro­longer le tableau con­tenant S, I et R jusqu’à ce que I devi­enne nul. La courbe R se ter­mine par une droite hor­i­zon­tale don­nant le taux d’infectés min­i­mal dans la pop­u­la­tion pour que l’épidémie s’arrête.

On remar­que que ce taux est très dépen­dant de R₀. Une série d’essais Excel avec des R₀ allant de 1 à 4 donne la courbe suivante.

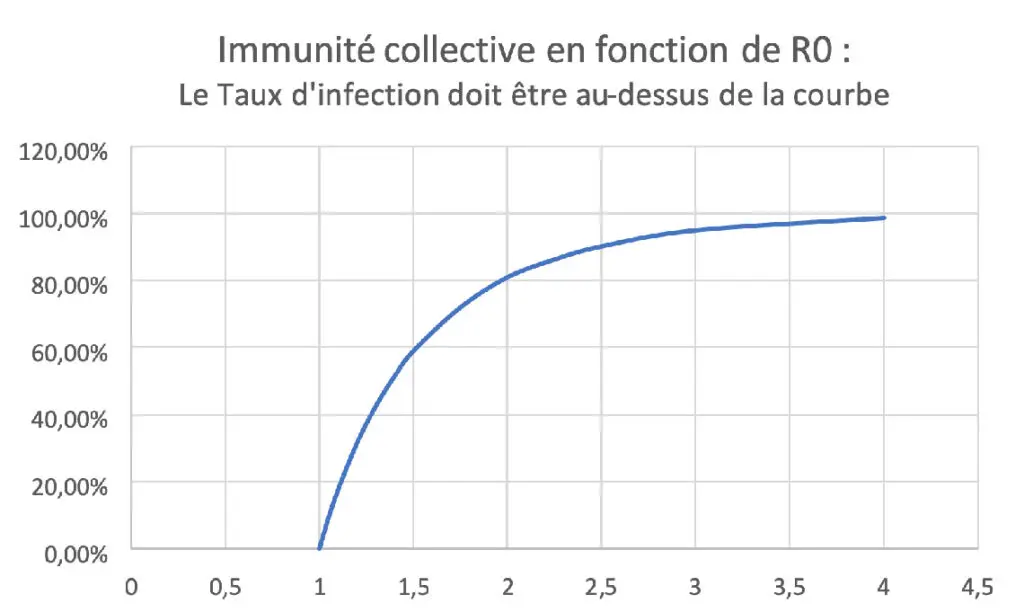
Les cours d’épidémiologie don­nent pour cette courbe l’équation suivante :

Taux_{col­lec­tive} = 1 — exp ( — R0 x Taux_{col­lec­tive} )

qui con­firme les résul­tats obtenus grâce à Excel, méth­ode qui ne demande aucune con­nais­sance math­é­ma­tique particulière.

Est donc inex­acte l’affirmation que l’on entend ou lit sou­vent, selon laque­lle pour attein­dre une immu­nité col­lec­tive il faut que le taux total de per­son­nes ayant été infec­tées dépasse 60 ou 70 %. La courbe mon­tre que, si une pop­u­la­tion réus­sit à main­tenir de façon durable un R₀ inférieur à 1,5, l’immunité col­lec­tive est obtenue pour des valeurs inférieures à 60 % (par exem­ple env­i­ron 40 % pour un R₀ de 1,3). La com­bi­nai­son d’un R₀ et d’un taux d’infection de la pop­u­la­tion per­me­t­tant de se posi­tion­ner au-dessus de la courbe per­met aus­si d’attendre l’arrivée d’un vac­cin, d’un remède ou d’une éventuelle muta­tion favor­able du virus. Il est pos­si­ble que cer­taines zones à forte den­sité de pop­u­la­tion soient actuelle­ment proches de cette immu­nité col­lec­tive (Stock­holm ?), mais s’y main­tenir de façon durable impose de ne pas laiss­er aug­menter le R₀ qui aura per­mis d’en bénéficier.

---

Articles similaires :

Mod­èles math­é­ma­tiques d’épidémies les plus élaborés : pourquoi leurs prévi­sions ini­tiales sont-elles sou­vent exces­sive­ment pessimistes ? SARS-CoV­‑2 : « Où est caché le loup ? » « Deux­ième vague » Covid-19 : per­spec­tives 2020–2021 Covid-19 : inter­ro­ga­tions sur le mod­èle épidémi­ologique,
Prise en compte de la vac­ci­na­tion et du « vari­ant anglais » Le défi du décideur face à l’incertitude Ges­tion de la crise Covid : la manie française de l’uniforme