Des régularités extraordinaires et irréfragables dans les observations interférométriques de Dayton C. Miller, 1925–1926,

Libres propos

Dossier : ExpressionsMagazine N°588 Octobre 2003

« Si les observations du Dr Miller étaient confirmées, la théorie de la relativité serait en défaut. L’expérience est le juge suprême. »

Albert Einstein
Revue Science, 1925

« L’attrait principal de la théorie de la relativité est qu’elle constitue un tout logique. Si une seule de ses conséquences se montrait inexacte il faudrait l’abandonner. »

Albert Einstein
Comme je vois le monde, 1939

« Tout ce que nous connaissons de la réalité vient de l’expérience et aboutit à elle. Des propositions purement logiques sont complètement vides à l’égard de la réalité […].
« Il résulte de là que nos conceptions du réel physique ne peuvent jamais être définitives. Si nous voulons être d’accord d’une manière logique, d’une manière aussi parfaite que possible avec les faits perceptibles, nous devons toujours être prêts à modifier ces conceptions, autrement dit le fondement axiomatique de la physique. De fait, un coup d’œil sur l’évolution de la physique nous permet de constater que ce fondement a subi au cours du temps de profonds changements. »

Albert Einstein
Comme je vois le monde, 1939

« Le physicien qui vient de renoncer à l’une de ses hypothèses devrait être plein de joie, car il vient de trouver une occasion inespérée de découverte. Son hypothèse, j’imagine, n’avait pas été adoptée à la légère : elle tenait compte de tous les facteurs connus qui semblaient pouvoir intervenir dans le phénomène. Si la vérification ne se fait pas, c’est qu’il y a quelque chose d’inattendu, d’extraordinaire : c’est qu’on va trouver de l’inconnu et du nouveau. »

Henri Poincaré
La Science et l’Hypothèse, 1906

« Lorsqu’il se produit une révision ou une transformation d’une théorie physique, on trouve qu’il y a presque toujours au point de départ la constatation d’un ou plusieurs faits qui ne pouvaient pas entrer dans le cadre de la théorie, sous sa forme actuelle. Les faits restent en effet toujours la clef de voûte de laquelle dépend la stabilité de toute théorie, si imposante qu’elle puisse être.
« Pour le théoricien vraiment digne de ce nom il n’y a d’ailleurs rien de plus intéressant qu’un fait en contradiction avec une théorie jusqu’alors tenue pour vraie, c’est alors que commence pour lui le vrai travail. »

Max Planck
Initiations à la Physique, 1941

NOTE DE LA RÉDACTION

Il y a sept ans a déjà été publié dans La Jaune et la Rouge un article de Maurice Allais sous le titre, Les expériences de Dayton C. Miller, 1925–1926 et la Théorie de la Relativité (août-septembre 1996, p. 29–37).

Cet article a été suivi de deux articles (juin-juillet 1997, p. 43–50 ; août-septembre 1997, p. 69–77) où l’auteur a répondu au très nombreux courrier qu’il a reçu de nos lecteurs.

Ces trois articles gardent aujourd’hui tout leur intérêt.
Nous ne saurions trop conseiller à nos lecteurs de s’y reporter. Toutefois nous estimons intéressant de publier aujourd’hui, sous une forme nouvelle, le réexamen par Maurice Allais des résultats des expériences effectuées par Dayton C. Miller en 1925–1926. Cette synthèse des Communications de Maurice Allais à l’Académie des sciences des 23 janvier 1997, 26 avril 1999 et décembre 2000 apporte en effet une cohérence et une force nouvelle à ses analyses.

Il va de soi que l’article de Maurice Allais ne peut manquer de susciter un très large débat et naturellement les remarques et questions de nos lecteurs seront reçues avec le plus grand intérêt.

A – LES OBSERVATIONS DE DAYTON C. MILLER – 1925–1926

1. Il est généralement admis que l’expérience interférométrique de Michelson¹ a toujours donné des résultats négatifs. En particulier les observations résultant des expériences de 1925–1926 de Dayton C. Miller², de loin les plus nombreuses, sont considérées par de très nombreux physiciens comme résultant d’un effet de température³.

Cependant l’examen approfondi des observations de Miller m’a conduit à la conclusion qu’elles présentent des régularités très remarquables qui excluent tout effet pervers de température. Pour simplifier je me borne dans cette Section à l’analyse des hodographes correspondant aux observations de Miller.

2. Le principe des expériences de Miller est le même que celui des expériences de Michelson. Suivant ce principe l’interféromètre permet de mesurer la différence de la vitesse de la lumière suivant deux directions perpendiculaires.

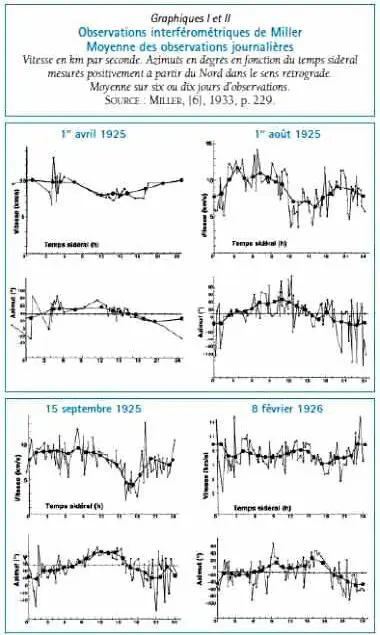
Dans son mémoire de 1933 Miller a présenté ses observations sous la forme de huit graphiques, quatre pour les vitesses et quatre pour les azimuts, en fonction du temps sidéral, pour quatre périodes d’observations continues d’une durée de six à huit jours ([6] 1933, p. 229).

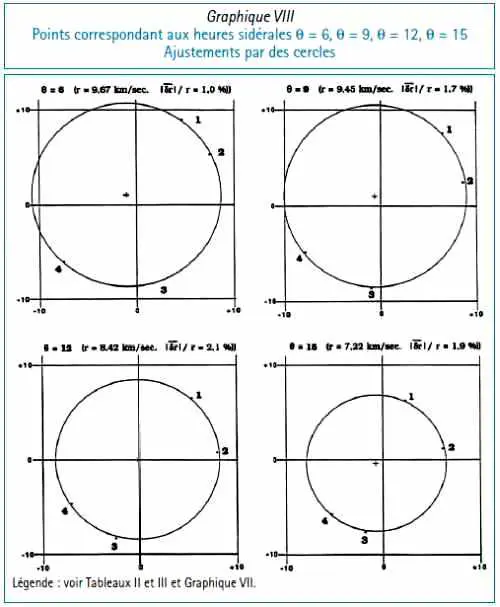
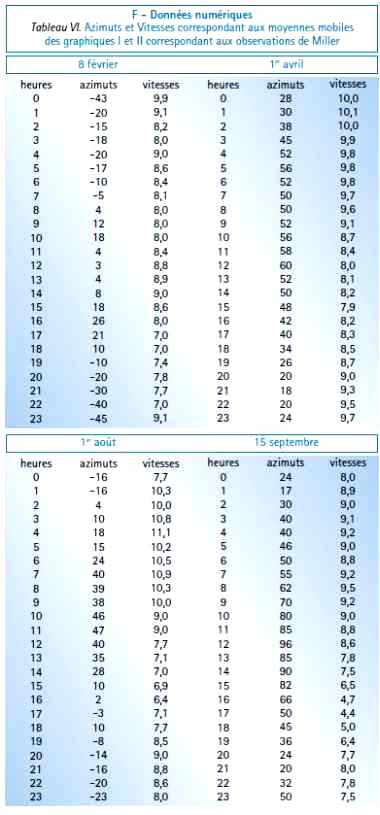
Sur ces huit graphiques Miller a indiqué à la fois les azimuts et les vitesses, et leurs moyennes mobiles. Sur les agrandissements photographiques des huit graphiques de Miller j’ai considéré pour chaque période d’observation les valeurs d’heure en heure des moyennes mobiles v et A des vitesses et des azimuts. Ces données numériques sont indiquées sur le Tableau VI de la Section F.

B – LA DÉTERMINATION DES HODOGRAPHES

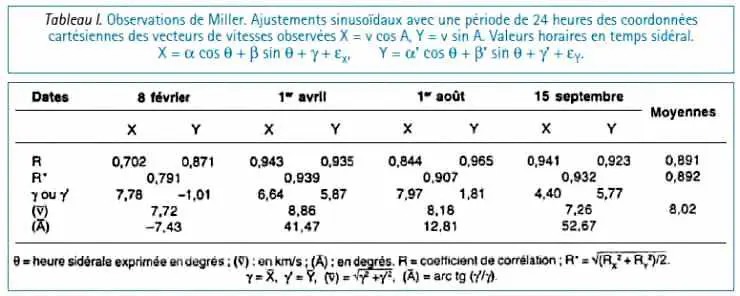
1. les coordonnées cartésiennes X et Y du vecteur vitesse v de coordonnées polaires v et A déterminées par l’interféromètre ont pour expressions : X = v cos A, Y = v sin A.

On peut calculer suivant la méthode des moindres carrés les ajustements diurnes, avec des sinusoïdes d’une période de 24 heures, des valeurs horaires de X et Y en fonction du temps sidéral, et avec les valeurs estimées X* et Y* de X et Y déterminer une estimation H* de l’hodographe H. Cet hodographe estimé est une ellipse dont le centre a pour coordonnées les moyennes ‾X et ‾Y⁴.

Les résultats de ces ajustements sont présentés sur le Tableau I. Au regard des approximations faites, les coefficients des corrélations multiples sont remarquablement élevés. Leur moyenne générale est égale à ‾R = 0,891.

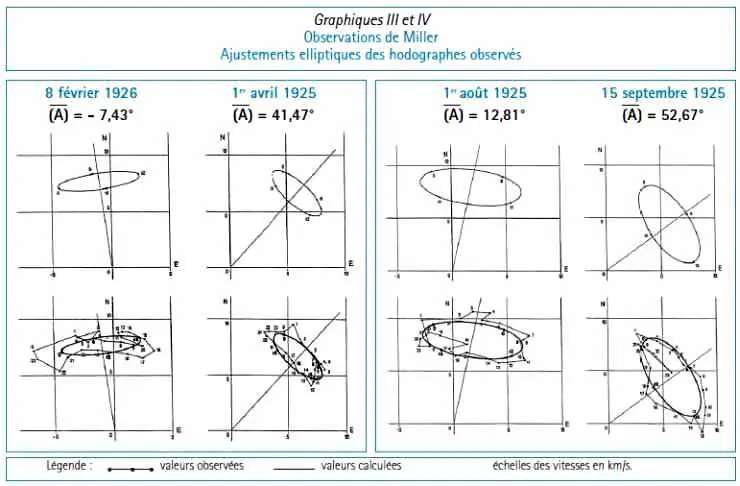
Les Graphiques III et IV représentent les ellipses représentatives des hodographes H* correspondant à ces ajustements. Pour chaque date sont représentés d’une part l’hodographe estimé H* et d’autre part la superposition de l’hodographe observé H et de l’hodographe estimé H*.

Dans l’ensemble la représentation des hodographes observés est tout à fait remarquable.

Il en est également de même des concordances de phase entre les hodographes calculés et observés.

On constate encore que les hodographes estimés sont presque exactement perpendiculaires aux directions moyennes ‾(A) des azimuts A⁵.

2. Toutes ces propriétés correspondent incontestablement à une très grande cohérence sous-jacente aux observations de Miller.

Leur signification est d’autant plus grande que les paramètres considérés ne correspondent pas à des observations isolées, mais à des moyennes de très nombreuses observations.

De là il résulte qu’il est tout à fait inexact de considérer que l’expérience de Michelson ait toujours donné des résultats négatifs.

3. En fait, cette analyse mène à deux conclusions :

La première, c’est qu’il existe une très grande cohérence, tout à fait indiscutable, entre les observations interférométriques de Miller, et qu’elle correspond à un phénomène bien réel.
La seconde, c’est qu’il est tout à fait impossible d’attribuer cette très grande cohérence à des causes fortuites, ou à des effets pervers (de température par exemple).

Ces conclusions sont indépendantes de toute hypothèse et de toute analyse théorique que ce soit.

Les résultats très significatifs sur lesquels elles s’appuient n’ont pas été aperçus par Miller, ni d’ailleurs par qui que ce soit.

C – D’EXTRAORDINAIRES RÉGULARITÉS

1. Dans la Section B j’ai calculé et analysé les hodographes elliptiques correspondant aux observations de Miller. Pour chacune des quatre périodes de Miller (8 février, 1^er avril, 1^er août, 15 septembre) l’hodographe elliptique a pour équation

X* = α cos θ + β sin θ + γ
Y* = α” cos θ + β” sin θ + γ”
où les α, β, γ, α”, β”, γ” diffèrent pour chaque période. Cependant il résulte du processus même de la détermination des vitesses par l’interféromètre que les vitesses ne sont déterminées qu’au signe près. Il en résulte que pour chacune des périodes T_j les équations des hodographes elliptiques doivent s’écrire :

X_j* = ε_j (α cos θ + β sin θ + γ)
Y_j* = εj (α” cos θ + β” sin θ + γ”)
avec : ε_j = ± 1.

Pour déterminer les quatre ε_j il convient de s’assurer que l’on passe d’une période à l’autre de manière cohérente. En avril 1998 cette analyse m’a conduit à conclure qu’il y a deux solutions :
(a) ε₁ = – 1 ε₂ = – 1 ε₃ = + 1 ε₄ = + 1
(b) ε₁ = + 1 ε₂ = + 1 ε₃ = – 1 ε₄ = – 1

La solution (b) est symétrique de la solution (a) par rapport à l’origine et elle se déduit de la solution (a) par une rotation de 180° par rapport à l’origine.

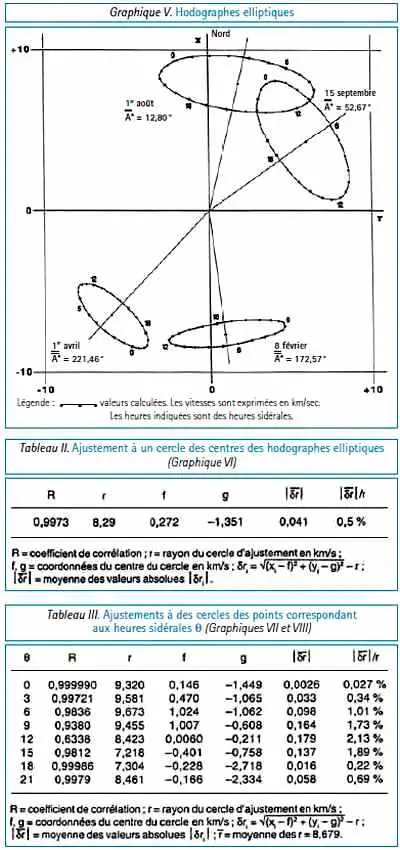
Le Graphique V représente l’ensemble des hodographes elliptiques correspondant aux conditions (a).

En exécutant ce graphique mon collaborateur Alain Villemur a constaté que les quatre centres des hodographes se placent très sensiblement sur un même cercle et qu’il en est de même pour chacun des huit groupes de quatre points correspondant à une heure sidérale donnée.

Ces déductions graphiques sont entièrement vérifiées par le calcul.

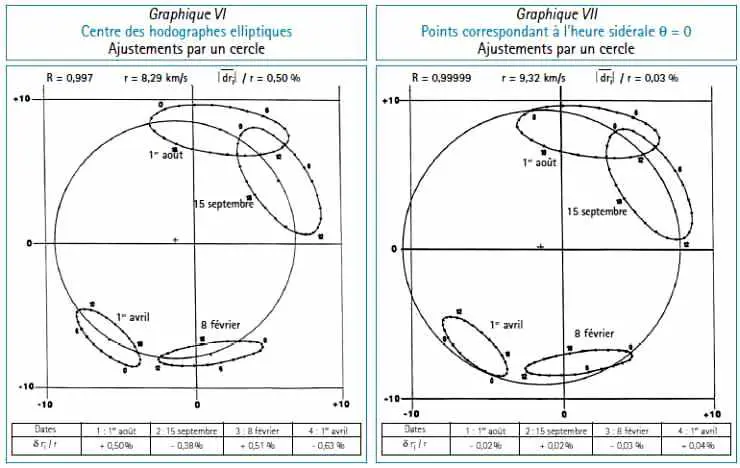
2. Les Tableaux II et III donnent les éléments des ajustements, par la méthode des moindres carrés, à des cercles d’une part des centres des hodographes, et d’autre part des huit groupes de quatre points aux heures sidérales de 3 heures en 3 heures⁶^{, 7}. Les écarts relatifs des ajustements sont tous très petits. Les Graphiques VI et VII représentent respectivement le cercle correspondant aux centres des hodographes et le cercle correspondant aux quatre points pour l’heure sidérale θ = 0.

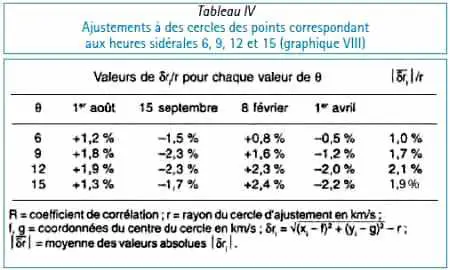Le Graphique VIII représente à titre d’illustration les quatre cercles correspondant aux heures sidérales θ = 6, 9, 12 et 15. Ce sont les moins bons ajustements, mais les écarts relatifs sont très petits, et les ajustements sont très significatifs (Tableau IV)^{8, 9}.

3. Ces nouvelles régularités, à vrai dire tout à fait extraordinaires et inattendues, et qui n’existent qu’en temps sidéral, viennent confirmer totalement les conclusions des paragraphes 2 et 3 de la Section B. Il est effectivement absolument impossible d’attribuer ces nouvelles régularités à des effets de température ou à des causes fortuites. Elles infirment tout aussi bien l’interprétation donnée par Miller à ses observations que les critiques qui ont dénié toute valeur aux observations de Miller.

D – L’ORIGINE DES RÉGULARITÉS CONSTATÉES

La présente Section a pour objet de discuter très brièvement l’origine effective des régularités que j’ai mises en évidence dans les observations interférométriques de Dayton C. Miller 1925–1926 : variations de température ou anisotropie de l’espace. Cette Section s’appuie notamment sur un certain nombre de faits très significatifs et entièrement nouveaux.

1. Aux notations près¹⁰, la formule utilisée par Miller [10] (p. 227) :

v = (d c²/2 D) ^¹⁄₂ (11)

pour calculer la différence de vitesse de la lumière dans un azimut donné et dans la direction perpendiculaire est entièrement valable¹¹. En fait, elle a été utilisée par Michelson et tous ses successeurs et elle est présentée dans tous les traités de physique¹².

Sa validité expérimentale a d’ailleurs été démontrée par le succès de l’expérience de Michelson et Gale en 1925 [3] qui a permis de mesurer la vitesse de rotation de la Terre à 2,6 % près (Allais, [9], p. 553).

2. En fait, en ce qui concerne les effets de température, Shankland et al. [7] ne présentent que des hypothèses et des raisonnements fragiles. Ils soulignent eux-mêmes que les données disponibles sur la température sont tout à fait insuffisantes pour élaborer toute analyse précise¹³. Ils écrivent en effet ([7], p. 175) :

« In what follows, we shall interpret the systematic effects on this basis, but must admit that a direct and general quantitative correlation between amplitude and phase of the observed second harmonic on the one hand and the thermal conditions in the observation hut on the other hand could not be established. The reason for this failure lies in the inherent inadequacy, for our purpose, of the temperature data available. »

2.1. Dans une discussion objective Shankland et al. [7] auraient dû tenir compte de ce qu’écrit Miller en 1933 sur les effets éventuels de la température au regard de toutes ses expériences antérieures ([6], p. 220) :

« An extended series of experiments was made to determine the influence of inequality of temperature in the interferometer room and of radiant heat falling on the interferometer… These experiments proved that under the conditions of actual observation, the periodic displacements could not possibly be produced by temperature effects. »

Miller était un très bon expérimentateur et il a analysé à fond tous les effets possibles de température, et cela dans des conditions expérimentales très différentes (Miller [6], p. 212, 218, 220, 221, et Allais [9], p. 411, 412).

Suivant Einstein lui-même Miller était un expérimentateur extrêmement compétent¹⁴ (Allais [9], p. 586, n. 7).

3. Mes calculs se sont bornés à analyser les moyennes mobiles des observations de vitesses et d’azimuts en temps sidéral telles qu’elles ont été publiées par Miller ([9], p. 388–389) (voir le Tableau VI, Section F).

3.1. Sur les lissages effectués par Miller Roger Balian ([12], p. 250) écrit :

« Ces procédés de lissage ont été conduits en imposant la contrainte que le résultat final soit une fonction périodique, de période 24 heures, du temps sidéral. Il n’est donc guère surprenant, après de tels lissages avec contrainte de périodicité, que les données soient ajustables par des ellipses. »

Cette affirmation est totalement erronée. Si on considère les mêmes données en temps civil on obtient en effet pratiquement les mêmes ellipses. Au cours d’une même période de six à huit jours les différences entre temps sidéral et temps civil sont en effet relativement négligeables, et une périodicité diurne sidérale est indiscernable d’une périodicité diurne solaire (Allais [9], p. 378, n.1)¹⁵.

Une différence entre temps civil et temps sidéral n’apparaît que sur des moyennes annuelles comme le démontre la comparaison des graphiques représentatifs des expériences d’Esclangon en temps sidéral et en temps civil (Esclangon [5], p. 52, et Allais [9] p. 380 et 381).

En fait, comme pour les observations d’Esclangon, les moyennes des quatre séries d’observations de vitesse et d’azimut de Miller ne présentent une périodicité diurne très marquée de 24 heures qu’en temps sidéral (Allais [9], p. 381 et 393). Voir tout particulièrement les Graphiques présentés par Miller lors de la Conférence du Mont Wilson en février 1927 ([4], p. 362).

Si les régularités constatées dans les observations de Miller résultaient d’un effet de température, elles ne se constateraient en moyenne qu’en temps civil et non en temps sidéral.

3.2. Le Tableau V ci-dessous indique les heures θ en temps sidéral et θ” en temps civil pour lesquelles l’azimut A est égal à sa valeur moyenne (A) (avec dA/dt < 0) et pour lesquelles la vitesse v passe par son minimum. Il indique également les valeurs absolues des écarts de θ et θ” avec leurs moyennes ‾θ et ‾θ”.

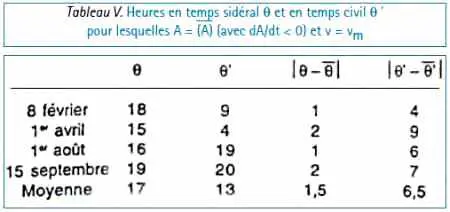On voit que les θ s’écartent relativement peu de leur moyenne (Allais [9], p. 393) alors que les θ” s’en écartent considérablement, en fait quatre fois plus (6,5÷1,5 = 4,3). Il résulte de là que les concordances de phase que l’on constate en temps sidéral ne se constatent pas en temps civil. C’est d’ailleurs ce qu’a souligné Miller ([6], p. 231).

Il résulte de là encore que les effets observés ont une origine cosmique et qu’ils sont, par là même et pour l’essentiel, indépendants des variations diurnes et annuelles de la température.

Il est dès lors totalement impossible de soutenir, comme le suggère Roger Balian [12], à la suite de Shankland [7], qu’une différence de température de 0,001° de la température de l’air dans l’espace des bras de l’interféromètre puisse suffire pour expliquer les régularités très significatives que j’ai mises en évidence dans les observations de Miller.

3.3. Au total l’affirmation de Roger Balian suivant laquelle « Il est difficile de tirer des conclusions des deux types de régularités signalées par M. Allais » ne repose sur aucune justification réelle¹⁶.

Que de simples perturbations de température puissent entraîner des régularités aussi marquées que celles présentées ci-dessus est manifestement totalement impossible¹⁷.

4. Quant aux expériences postérieures aux expériences de Miller sur lesquelles s’appuie Roger Balian (Allais [9], p. 415–416, et Miller [6], 1933, p. 239–240) elles se sont bornées à des observations limitées faites à un instant donné pour tester des hypothèses spécifiques.

En fait, aucune de ces expériences n’a reposé sur des observations continues de jour et de nuit au cours de différentes périodes de six à huit jours au cours d’une même période de douze mois comme cela a été le cas des expériences de Miller en 1925–1926 et qui ont comporté en tout 6 400 tours d’horizon avec 200 000 lectures au cours de quatre périodes de six à huit jours (Allais [9], p. 416).

4.1. En tout cas il y a lieu de considérer également les expériences interférométriques de Michelson, Morley, et Miller antérieures aux expériences de 1925–1926 de Miller. On constate en effet qu’il n’y a aucune contradiction entre les résultats de Miller et les résultats précédents de Michelson et Morley (Allais [9], p. 414).

Dans son mémoire de 1933 ([4], p. 207) Miller illustre sur un graphique la compatibilité des résultats des expériences de 1887 de Michelson et Morley, et de 1902, 1904 et 1905 de Morley et Miller avec les résultats qu’il a obtenus en 1925–1926. Dans tous les cas les vitesses sont de l’ordre de 8 à 9 km/s à des heures sidérales comparables. Tout particulièrement l’expérience de Michelson et Morley de 1887 donnait une estimation de 8 km/s pour la vitesse, résultat interprété à tort à l’époque comme correspondant à une erreur de mesure.

Cette comparaison (dont Shankland et al. [7] omettent totalement de tenir compte) montre que les effets constatés, indûment attribués à des circonstances fortuites, sont en réalité tous du même ordre de grandeur de 8 km/s pour la vitesse (Miller [6], p. 206–207).

Si donc ces effets devaient être considérés comme des effets de température, il faudrait admettre que les effets de température auraient été les mêmes, de l’ordre de 8 km/s, en 1887, 1902, 1904, 1905 et 1925 alors que les situations géographiques à Cleveland et au Mont Wilson différaient totalement et que les appareillages et les conditions expérimentales étaient très différents dans toutes ces expériences, ce qui est manifestement totalement impossible.

4.2. Il convient de souligner qu’à aucun moment Roger Balian [12] ne met en doute la correction des calculs que j’ai effectués à partir des données de Miller et qu’il se limite à dire que « la question essentielle est de déterminer la cause physique » des variations constatées des observations.

Comme l’explication par les variations de température, seule explication considérée par Roger Balian, doit être exclue pour toutes les raisons ci-dessus, il faut incontestablement conclure que les régularités constatées dans les observations de Miller résultent des variations de la vitesse de la lumière suivant sa direction¹⁸.

E – LES THÉORIES DE LA RELATIVITÉ RESTREINTE ET DE LA RELATIVITÉ GÉNÉRALE TOTALEMENT INVALIDÉES PAR LES DONNÉES DE L’OBSERVATION

De tout ce qui précède résulte en toute certitude la validité de quatre propositions :

la première, c’est qu’il existe une très grande cohérence tout à fait indiscutable dans les observations interférométriques de Miller et qu’elle correspond à un phénomène bien réel ;
la seconde, c’est qu’il est tout à fait impossible d’attribuer cette très grande cohérence à des causes fortuites, ou à des effets pervers (de température par exemple) ;
la troisième, c’est que la vitesse de la lumière n’est pas invariante quelle que soit sa direction.
Il en résulte dès lors que la théorie de la relativité restreinte d’Einstein qui repose fondamentalement sur un principe, l’invariance de la vitesse de la lumière, est contredite par les données de l’observation¹⁹.
la quatrième, c’est que la théorie de la relativité générale, dont la théorie de la relativité restreinte n’est qu’un cas particulier, est également infondée²⁰^{, 21}.

G – RÉFÉRENCES (par ordre chronologique)

[1] Michelson A., 1881. The Relative Motion of the Earth and the Luminiferous Aether, The American Journal of Science, Third Series, Vol. XXII, Art. XXI, p. 120–129.

[2] Michelson A. and Morley E., 1887. On the Relative Motion of the Earth and the Luminiferous Aether, The American Journal of Science, Third Series, Vol. XXIV, n° 203, Art. XXXVI, p. 333–345.

[3] Michelson A., and Gale H., The effect of the Earth’s rotation on the velocity of light, Astrophys. J. (1925) p. 137–145.

[4] Conference on the Michelson-Morley Experiment, 4–5 February 1927, Astrophys. J. LXVIII (1928) p. 341–402.

[5] Esclangon E. Sur l’existence d’une dissymétrie optique de l’espace, J. Observ. XI (4) (1928) p. 49–63.

[6] Miller Dayton C., 1933. The Ether-Drift Experiment and the Determination of the Absolute Motion of the Earth, Review of Modern Physics, Vol. 5, July 1933, n° 3, p. 203–242.

[7] Shankland Robert S., Mc Cuskey S.W., Leone E.C. and Kuersi G., 1955. New Analysis of the Interferometer Observations of Dayton C. Miller, Reviews of Modern Physics, Vol. 27, p. 167–178.

[8] Foch A., Mécanique, Masson, 1967.

[9] Allais M., L’Anisotropie de l’Espace, Éditions Clément Juglar (62 av. de Suffren. 75015-Paris), 1997, 758 p.

[10] Allais M., C.R. Acad. Sci. Paris Sér. IIb 327 (1999), p. 1405–1 410.

[11] Allais M., C.R. Acad. Sci. Paris Sér. IIb 327 (1999), p. 1411–1 419.

[12] Balian R., C.R. Acad. Sci. Paris Sér. IV 1 (2000), p. 249–250.

[13] Allais M., C.R. Acad. Sci. Paris Sér. IV (2000), p. 1205–1 210.

__________________________________________________
1. Michelson, 1881, [1], et Michelson et Morley, 1887, [2].

2. Miller, 1933, [6].

3. Voir notamment Shankland et al. 1955, [7].

4. On considère les 24 séries de valeurs de X et Y correspondant aux 24 valeurs horaires en temps sidéral q : 0, 1, …, 23.
Les deux corrélations considérées s’écrivent :
X = α cos θ + β sin θ + γ + εX (1)
Y = α” cos θ + β” sin θ + γ” + εY (2)
θ désigne l’heure sidérale, exprimée en degrés, égale à la valeur horaire multipliée par 15. Les a, b, a”, b” désignent les coefficients de régression.
Comme les valeurs moyennes de cos θ et sin θ sont nulles, on a
γ = ‾X γ” = ‾Y (3)
où ‾X et ‾Y représentent les valeurs moyennes de X et Y. Les quantités εX et εY désignent les résidus des deux corrélations.
On a naturellement
X* = α cos θ + β sin θ + γ (4)
Y* = α” cos θ + β” sin θ + γ” (5)
où X* et Y* représentent les valeurs estimées de X et Y.
Les relations linéaires (4) et (5) permettent de déterminer cos θ et sin θ en fonction linéaire de X* et Y*, et en portant ces valeurs de cos θ et sin θ dans la relation d’identité :
cos² θ + sin² θ = 1 (6)
on obtient une équation du second degré en X* et Y*. Il résulte de là que l’hodographe ainsi estimé est une ellipse dont le centre a pour coordonnées les valeurs moyennes ‾X et ‾Y de X et Y. L’angle ‾(A) joignant l’origine à ce centre a pour expression :
‾(A) = arc tg (‾Y / ‾X) (7)

5. Dans le cas le plus général, et suivant la théorie classique, l’hodographe de la projection de la vitesse de la Terre (vitesse orbitale plus vitesse cosmique) sur le plan horizontal est une ellipse symétrique par rapport au méridien dont le grand axe est perpendiculaire au méridien, et dont le rapport du petit axe au grand axe est égal à sinφ, φ désignant la latitude du lieu.
En comptant les abscisses x le long du méridien positivement vers le Nord et les ordonnées y sur la perpendiculaire au méridien positivement vers l’Est, l’équation classique de l’hodographe est :
( (x ‑V sinδ cosφ) / sinφ) ² + y² = V² cos² δ (8)
où V est la vitesse totale de la Terre et δ sa déclinaison, et où φ est la latitude du lieu d’observation. Comme la déclinaison δ varie suivant l’époque considérée de l’année, il en est de même de l’hodographe, qui reste cependant toujours symétrique par rapport au méridien.
Les Graphiques III et IV infirment donc la théorie classique.

6. Le principe des ajustements est très simple. Considérons en effet un cercle de rayon r et dont le centre a pour coordonnées f et g. On a pour tout point (X, Y) du cercle (X — f)² + (Y — g)² = r². Dès lors que l’on considère la corrélation X² + Y² = AX + BY + C + ε, on a f = A/2, g = B/2, r² = C + f² + g².

7. Pour les huit cercles correspondant aux huit heures sidérales considérées les coefficients de corrélation sont tous très élevés sauf pour le cercle correspondant à θ = 12 heures sidérales. Cependant pour ce cercle l’écart relatif moyen ‾|δ r| / r n’est que de 2 %. Pour l’ensemble des huit cercles la valeur moyenne des écarts relatifs ‾|δ r| / r n’est que de 1 % (Tableau III).

8. L’analyse harmonique de la distribution sur ces cercles des points correspondant aux quatre dates de Miller met en évidence des régularités très remarquables correspondant à des ajustements sinusoïdaux centrés sur l’équinoxe de printemps du 21 mars.

9. Les hodographes calculés en temps civil sont très voisins des hodographes calculés en temps sidéral. Il en est donc de même du cercle, lieu des centres des hodographes.
Par contre les ajustements à des cercles des points correspondant aux huit heures civiles, correspondant aux huit heures sidérales considérées, sont très différents. Ils sont relativement mauvais et irréguliers. En fait, les régularités du Tableau III n’existent qu’en temps sidéral.

10. La notation v, universellement adoptée, est très fâcheuse et elle ne peut que susciter de très regrettables confusions.
Elle dérive en effet de l’hypothèse implicite que la différence mesurée de vitesse est égale à la vitesse de la Terre par rapport à l’éther. C’était là l’idée fixe de tous les expérimentateurs et de tous les commentateurs de l’expérience de Michelson.
En réalité il faudrait réécrire la formule classique (11) sous la forme Δv = (d c²/2 D) ^¹⁄₂
où Δv représente la différence mesurée de la vitesse de la lumière dans l’azimut considéré et dans la direction perpendiculaire.
Aujourd’hui l’hypothèse d’un éther immobile au sein duquel la Terre se déplacerait doit être considérée comme totalement contredite par les données de l’observation (Allais [9], p. 417–424).

11. Pour une analyse approfondie des observations de Miller, voir Allais [9], 1997, L’Anisotropie de l’Espace, p. 382–432 et 452–492. Sur les relations des observations de Miller avec la théorie classique et la théorie de la relativité d’Einstein, voir Allais [9] p. 547–644.

12. Sur l’analyse harmonique de ses observations Miller a donné toutes les indications utiles ([6], p. 206, 207, 226, 227 et 238).

13. Trop souvent les affirmations de Shankland et al. sont dénuées de toute justification. Ainsi, après avoir souligné à juste titre l’incompatibilité avec la théorie admise des écarts entre les moyennes A des azimuts avec la direction du méridien ils écrivent ([7], p. 172 ) :
« Under these circumstances little significant can be attached to the remarkable agreement between Miller’s Tables I and II (Miller [6], p. 230). »
C’est là une conclusion totalement erronée. Ce que mettent en cause en effet les valeurs différentes de zéro des moyennes A des azimuts ce n’est pas la validité des observations de Miller, mais la validité du Modèle considéré (Allais [9], p. 417–419).

14. Miller a été élu en 1921 membre de la National Academy of Sciences et il était en 1925 President of the American Physical Society.

15. Si de simples lissages peuvent permettre de déterminer l’amplitude d’une composante périodique si elle existe, ils ne peuvent en aucun cas la créer.

16. Pour le moins Roger Balian aurait dû démontrer comment selon lui des variations de température pourraient expliquer les extraordinaires régularités en temps sidéral (répartition sur un même cercle des points des quatres hodographes correspondant à une même heure sidérale) présentées ci-dessus.

17. Il faut en conclure qu’il est tout à fait inexact d’affirmer que l’expérience de Michelson a toujours donné des résultats négatifs (voir, par exemple, A. Foch [8] Chapitre XXX, Notion de Mécanique Relativiste, p. 695 ; voir également Allais [9], p. 577–586).

18. Il n’y a aucune commune mesure entre « la corrélation qualitative » de Shankland et al. dont fait état Roger Balian et la précision des calculs présentés ci-dessus.
Il convient d’ailleurs de souligner qu’il ne s’agit pas d’une » hutte « , mot employé indûment par Roger Balian pour désigner les locaux utilisés au Mont Wilson par Miller, mais d’une construction (Ether-drift house ») dont la photographie est donnée par Miller [6], Fig. 15, p. 221.

19. En fait les observations de Miller infirment également la Théorie classique et le Modèle utilisé par Miller ([6], p. 417–424 ). Ce qu’elles mettent en évidence c’est une Anisotropie de l’Espace.

20. Dans un prochain article, L’effondrement de la Théorie de la Relativité, Implications et Nouvelles Perspectives, j’analyserai les implications et la signification de l’invalidation de la théorie de la relativité au regard notamment des autres expériences invalidant à la fois la théorie de la relativité et les théories classiques (Allais [9], L’Anisotropie de l’Espace, 1997).
Quant aux déductions de la théorie de la relativité qui ont fait l’objet de vérifications expérimentales, il est certain que d’autres explications ont déjà été ou pourront être données (voir Allais [9], p. 629–633).

21. En fait, l’intolérance aveugle et fanatique de certains partisans de la théorie de la relativité ont fait perdre un siècle à la pensée physique.

N.D.L.R. : cet article a paru dans la revue Fusion de mai-juin 2003.