« Deuxième vague » Covid-19 : perspectives 2020–2021

L’utilisation d’Excel appliquée à la ver­sion la plus sim­ple du tra­di­tion­nel mod­èle SIR de Ker­ma­ck et McK­endrick per­met à des non-math­é­mati­ciens de mod­élis­er très facile­ment et de façon fidèle la sit­u­a­tion française jusqu’à fin octo­bre 2020. La cor­rec­tion d’une équa­tion de ce mod­èle de 1927 améliore la con­for­mité du mod­èle avec la réal­ité observée dans cette épidémie, ce qui per­met de mieux éval­uer les risques d’évolution fin 2020 et début 2021.

Aux lecteurs : pren­dre con­nais­sance avant de lire cet arti­cle de : https://www.lajauneetlarouge.com/covid-19-une-modelisation-simple-utilisant-excel-accessible-aux-non-mathematiciens-et-pleine-denseignements/ (J&R n° 758 d’octobre 2020) en sautant le dernier para­graphe sur l’immunité col­lec­tive qui est repris de façon plus explicite dans l’annexe 2 du présent article.

Rappel

Dans la ver­sion en ligne du n° 758 de La Jaune et la Rouge (octo­bre 2020) fig­urent deux arti­cles sur la mod­éli­sa­tion math­é­ma­tique des épidémies.

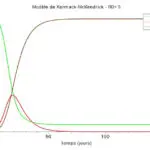
Le deux­ième inti­t­ulé « Une mod­éli­sa­tion sim­ple util­isant Excel … » inclut le dia­gramme suivant :

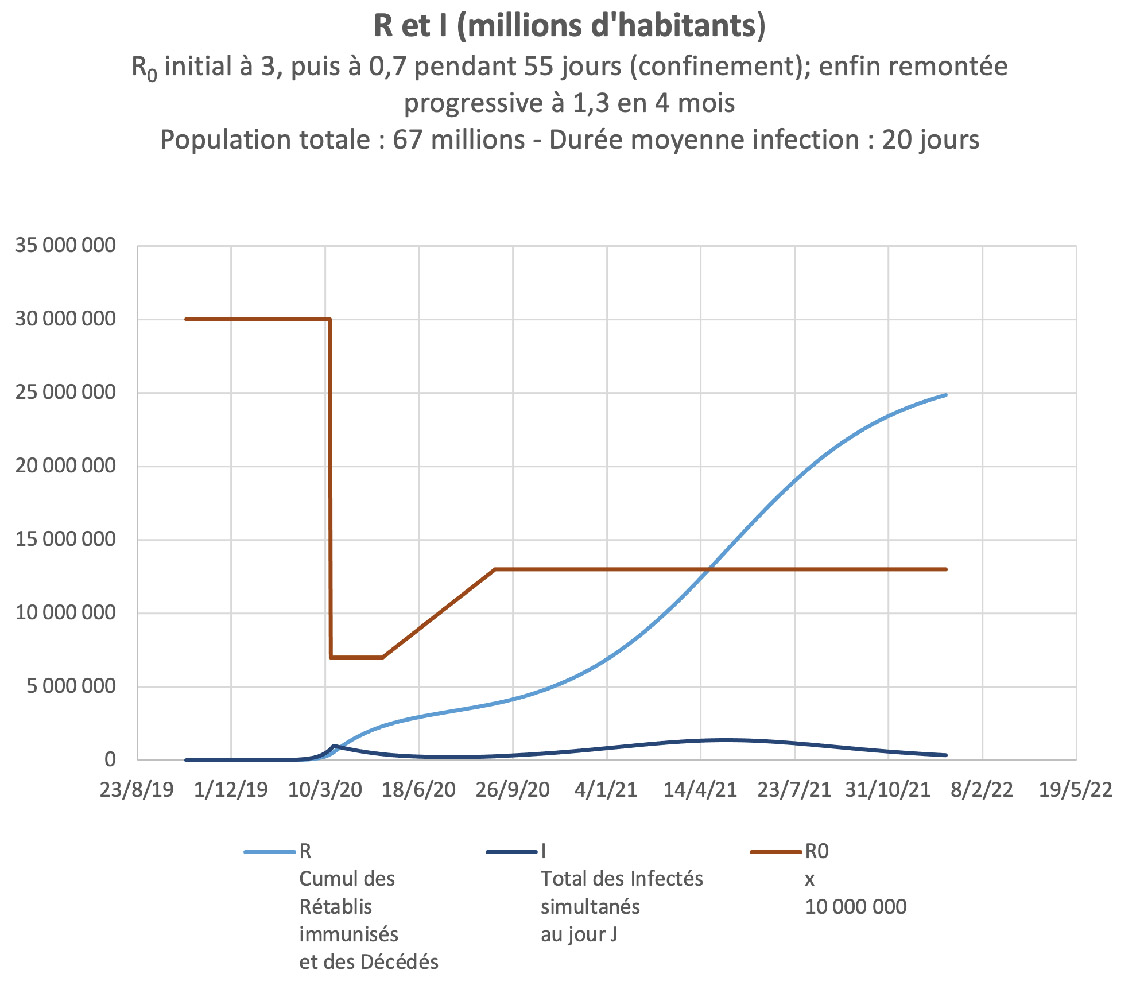
Ce dia­gramme est basé sur l’utilisation du mod­èle clas­sique SIR de Ker­ma­ck et McK­endrick et l’hypothèse d’une évo­lu­tion de R₀ pas­sant de 3 avant la pandémie à 0,7 pen­dant le con­fine­ment (17 mars – 11 mai), puis d’une remon­tée pro­gres­sive jusqu’à 1,3.

Si R₀ se sta­bil­i­sait ensuite de façon durable à cette valeur de 1,3, on con­stat­erait une remon­tée de l’épidémie à par­tir de l’automne 2020 jusqu’au début de l’été 2021, moment où serait atteint le seuil d’immunité col­lec­tive cor­re­spon­dant à R = 1,3 (voir annexe 2).

“Si R₀ se stabilisait de façon durable à cette valeur de 1,3,
on constaterait une remontée de l’épidémie à partir de l’automne 2020
jusqu’au début de l’été 2021.”

Avait été indiqué dans les deux arti­cles de la J&R d’octobre com­bi­en l’une des équa­tions de 1927 (util­isée dans tous des cours d’épidémiologie !) parais­sait, pour repren­dre un qual­i­fi­catif util­isé dans un autre con­texte par le Pr Didi­er Raoult, « foireuse ». Il s’agit de celle qui rend compte du débit de sor­tie (par guéri­son immu­nisante ou décès) du « com­par­ti­ment des infec­tés » qui serait pro­por­tion­nelle à tout instant au nom­bre I des infec­tés divisé par D, durée moyenne de l’infection pen­dant laque­lle les indi­vidus sont réputés contagieux.

Si cette approx­i­ma­tion est jus­ti­fiée en régime établi d’arrivée et de sor­tie d’individus dans I, elle est inex­acte en régime dynamique, où elle devrait être rem­placée par une équa­tion exp­ri­mant que les indi­vidus de I qui arrê­tent d’être con­tagieux à l’instant t sont ceux qui ont été infec­tés à l’instant (t – D), D étant la durée moyenne séparant leur infec­tion de leur guéri­son ou de leur décès.

Pour pren­dre en compte cette remar­que, il suf­fit de rem­plac­er dans les équa­tions tra­di­tion­nelles de 1927 :

dR(t)/dt = γ I (t) (mod­élisé en util­isant Excel)

par

dR(t)/dt = — dS(t – D)/dt (dont la mod­éli­sa­tion via Excel est tout aus­si simple)

ce qui, de façon intu­itive, cor­re­spond beau­coup mieux à la sim­u­la­tion d’un phénomène où tous les indi­vidus passent à peu près le même temps dans le « com­par­ti­ment I ».

Les ordi­na­teurs n’existant pas en 1927, Ker­ma­ck et McK­endrick ont vraisem­blable­ment préféré se rac­crocher à la forme clas­sique de la pre­mière équa­tion dif­féren­tielle, ce qui leur a per­mis, ain­si qu’à leurs suc­cesseurs, d’obtenir un cer­tain nom­bre de con­clu­sions par des méth­odes de pur raison­nement math­é­ma­tique, sans avoir besoin de recourir aux fas­ti­dieux cal­culs manuels itérat­ifs néces­saires à l’époque pour trac­er les courbes de S, I et R.

Observations sur le développement de l’épidémie fin octobre 2020

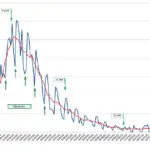
La baisse du nom­bre de per­son­nes infec­tées pen­dant l’été 2020 prévue par le mod­èle (mal­heureuse­ment non mesurable, sauf à utilis­er des tech­niques de sondage, ce qui n’a pas été fait pour des raisons inex­plic­a­bles) a bien été con­statée au niveau de ses con­séquences sur les hos­pi­tal­i­sa­tions et les décès, et a même per­mis à cer­tains de dire que l’épidémie était en train de s’éteindre d’elle-même. Mais depuis sep­tem­bre, la sit­u­a­tion a beau­coup changé : le nom­bre de morts Covid dans les hôpi­taux, qui est l’information la plus fiable, con­naît depuis cette époque une hausse de type expo­nen­tiel (voir fig­ure), certes beau­coup plus lente que celle de mars 2020, mais qui néan­moins amène notre pays à déplor­er fin octo­bre plus de 200 décès Covid quo­ti­di­ens, soit déjà le tiers du pic de la « pre­mière vague » sur­venu une ving­taine de jours après le début du pre­mier confinement.

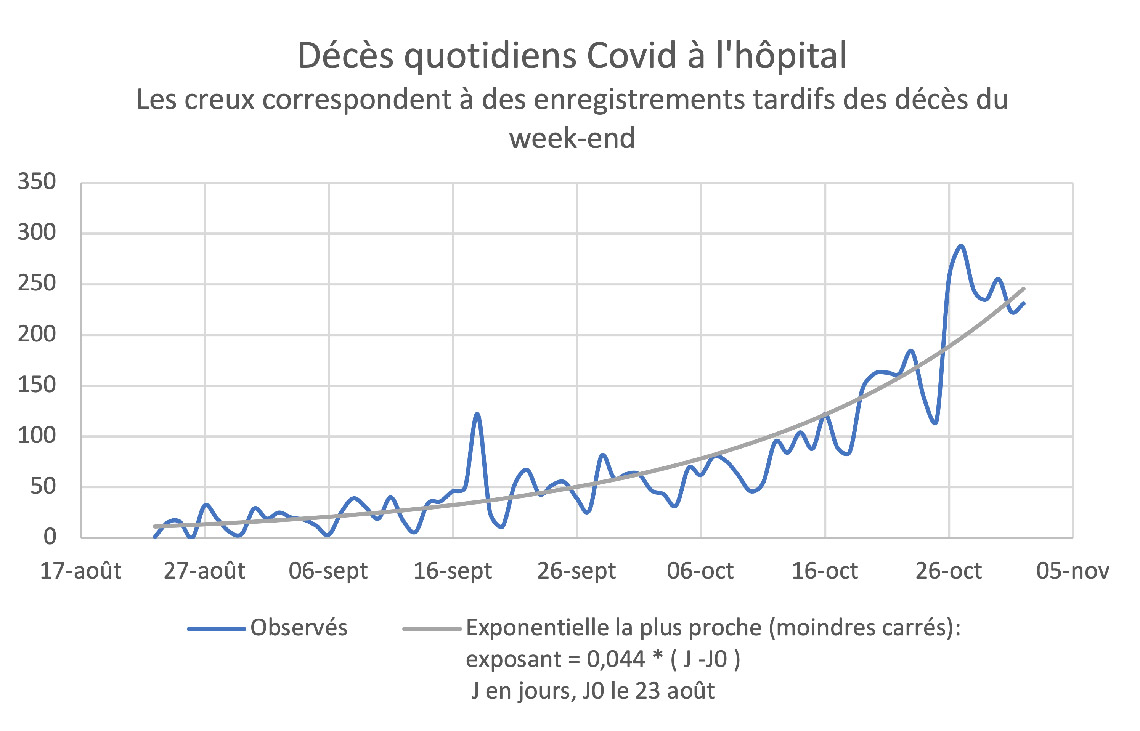
Ceci amène immé­di­ate­ment deux questions :

• le coef­fi­cient R₀ serait-il mon­té au-dessus de 1,3 ?
• que se passe-t-il si on replace l’équation « foireuse » du SIR clas­sique de 1927 par celle sug­gérée plus haut ?

Mon­tée de R₀ au-dessus de 1,3 ?

(une fois de plus, bien not­er que la nota­tion tra­di­tion­nelle R₀ n’a rien à voir avec R(0), nom­bre d’individus dans le com­par­ti­ment R à l’instant 0).

Rap­pelons d’abord ce que sig­ni­fient les dif­férentes ver­sions de R.

R₀ est le nom­bre moyen de cas sec­ondaires pro­duits pen­dant toute la durée de son infec­tion par un infec­tieux placé dans une pop­u­la­tion saine sus­cep­ti­ble d’être infec­tée (donc non vac­cinée et ne béné­fi­ciant pas – si ce cas existe – d’une immu­nité naturelle l’empêchant d’être infec­tée puis contagieuse).

Rap­pelons que R₀ est égal au nom­bre quo­ti­di­en de ren­con­tres poten­tielle­ment con­t­a­m­i­nantes d’un infec­té avec n’importe quel autre mem­bre de la pop­u­la­tion mul­ti­plié par la pro­por­tion de ces ren­con­tres débouchant sur une infec­tion réelle puis divisé par le nom­bre moyen de jours entre infec­tion et guéri­son ou décès.

R_effec­tif (nom­bre de repro­du­tion effec­tif) est égal à R₀ à deux conditions :

(voir à ce sujet la page 5 de la note de 14 pages présen­tée par Cédric Vil­lani à l’Office par­lemen­taire d’évaluation des choix sci­en­tifiques et tech­nologiques le 30 avril 2020)

• l’ensemble de la pop­u­la­tion est sus­cep­ti­ble d’être con­t­a­m­iné. Dans le cas con­traire (par­tie de la pop­u­la­tion vac­cinée ou ne pou­vant être ren­due con­tagieuse par infec­tion) il est pos­si­ble d’introduire via Excel au moment oppor­tun cette pop­u­la­tion dans le « com­par­ti­ment R » sans pass­er par le « com­par­ti­ment I » et de main­tenir pour l’autre par­tie de la pop­u­la­tion un coef­fi­cient R_effec­tif égal à R₀.
• les indi­vidus infec­tés ne sont pas sys­té­ma­tique­ment isolés de façon effi­cace. Dans cer­tains pays, un indi­vidu détec­té posi­tif ou même ayant sim­ple­ment eu un con­tact avec une per­son­ne infec­tée est sys­té­ma­tique­ment mis sans délai en quar­an­taine sévère, par exem­ple dans une cham­bre d’hôtel. Ce n’est pas le cas de la France (en dehors de quelques cas par­ti­c­uliers tels que l’équipage et les pas­sagers de navires).

Compte tenu de ce qui précède et de la sit­u­a­tion actuelle en France, dans la suite de cet arti­cle aucune dis­tinc­tion ne sera faite entre R₀, R_effec­tif et R.

Les doc­u­ments disponibles sur Inter­net don­nent la courbe suiv­ante pour l’évolution de R_effec­tif depuis le décon­fine­ment de mai (avant le con­fine­ment R était d’environ 3 ; durant le con­fine­ment d’environ 0,7). À not­er la baisse inex­pliquée d’août‑septembre suiv­ie de la remon­tée d’octobre.

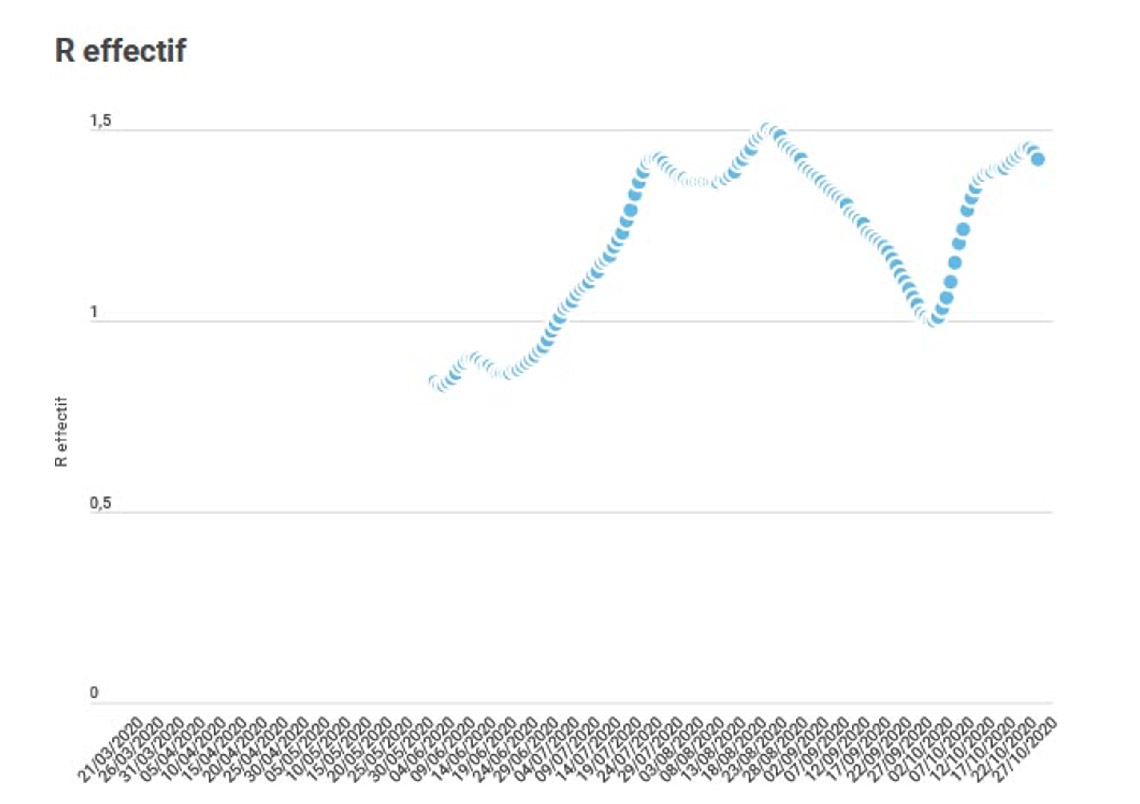
Conséquences sur le développement de l’épidémie

Modélisation utilisant Excel 

(voir tableaux Excel en annexe 1)

Nous con­sta­tons que le R_effec­tif à la sor­tie du con­fine­ment est mon­té net­te­ment plus haut que le 1,3 ini­tiale­ment prévu. Plusieurs caus­es sont pos­si­bles : bras­sage de pop­u­la­tion dû aux vacances d’été puis à la ren­trée sco­laire, volon­té de retrou­ver rapi­de­ment une vie qua­si-nor­male, sen­ti­ment d’absence de risque entretenu par cer­tains mem­bres du corps médi­cal affir­mant avec con­vic­tion que l’épidémie était ter­minée, ral­liement à cette idée via les réseaux soci­aux d’une frange impor­tante de la population.

Si R restait après le 1^er novem­bre au niveau 1,45 atteint vers la fin octo­bre 2020, l’utilisation des équa­tions SIR de 1927 don­nerait le dia­gramme suiv­ant qui tient compte des vari­a­tions de R con­statées depuis mai 2020 :

On voit que ce dia­gramme rend bien compte du creux dans la courbe I représen­tant le nom­bre d’infectés simul­tanés pen­dant l’été 2020, suivi d’une remon­tée à par­tir de sep­tem­bre. Néan­moins ces mou­ve­ments à la baisse puis à la hausse sem­blent timides par rap­port à la réal­ité observée. Il paraît donc intéres­sant de voir si le mod­èle SIR béné­fi­ciant de la cor­rec­tion (a pri­ori rel­a­tive­ment min­ime) pro­posée dans les arti­cles de la J&R d’octobre donne une meilleure représen­ta­tion de ce qui s’est passé jusqu’à maintenant.

Le rem­place­ment dans Excel de

dR(t)/dt = γ I (t)

par

dR(t)/dt = — dS(t – D)/dt

ne pose aucune dif­fi­culté (voir annexe 1) et donne de façon inat­ten­due pour le nom­bre d’infectés simul­tanés une forte accen­tu­a­tion de la baisse de l’été puis de la hausse de l’automne, net­te­ment plus con­formes à la réal­ité observée jusqu’à maintenant.

Pour le 1^er semes­tre 2021 il indique, si R reste égal à 1,45, une hausse à la fois plus rapi­de et plus impor­tante du nom­bre d’infections que le mod­èle SIR de 1927.

Cette pro­priété con­statée empirique­ment en util­isant Excel est con­fir­mée par l’étude fig­u­rant dans le blog de David Madore (ancien de l’ENS Ulm, pro­fesseur de math­é­ma­tiques à Télé­com Paris) qui est arrivée à une con­clu­sion sem­blable par une méthode dif­férente en com­para­nt les deux types de mod­éli­sa­tion (effec­tuées à R con­stant) : SIR tra­di­tion­nel (qu’il appelle « rétab­lisse­ment en proces­sus expo­nen­tiel ») et SIR mod­i­fié suiv­ant la même cor­rec­tion que celle pro­posée dans l’article (« rétab­lisse­ment en temps con­stant »). Les deux courbes qui suiv­ent font appa­raître ce que l’utilisation d’Excel avait per­mis de met­tre en évi­dence : le change­ment d’équation n’est pas anodin et mod­i­fie de façon assez sig­ni­fica­tive les courbes S (verte), I (rouge) et R (bleue), la courbe de vari­a­tion de I étant plus « pointue ».

Conclusions — Perspectives

Si R reste à son niveau actuel, il existe un risque impor­tant de forte aug­men­ta­tion du nom­bre d’infectés pen­dant la fin de 2020 et la pre­mière moitié de 2021. Il sem­ble donc vraisem­blable que les pou­voirs publics chercheront dans l’immédiat à faire repass­er R en-dessous de 1 « quoi qu’il en coûte ». Mais ceci ne règle pas le prob­lème de façon défini­tive : les con­fine­ments ne peu­vent pas être éternels …

Alors quelles sont les issues ?

Un miracle …

Pour­raient sur­venir des muta­tions ren­dant la Covid-19 moins con­tagieuse ou moins vir­u­lente. On pour­rait égale­ment décou­vrir qu’une par­tie impor­tante de la pop­u­la­tion béné­fi­cie d’une immu­nité naturelle… et tir­er immé­di­ate­ment des mod­èles épidémi­ologiques les con­clu­sions per­me­t­tant de guider une mod­i­fi­ca­tion de la poli­tique sanitaire.

La recherche de l’immunité collective

Si nous revenons à l’absence de con­traintes du mode de vie que nous con­nais­sions avant l’épidémie, le R₀ Covid-19 cor­re­spon­dant est de l’ordre de 3. La courbe de l’annexe 2 mon­tre qu’à ce niveau, les deux tiers de la pop­u­la­tion devront avoir été con­t­a­m­inés avant que l’épidémie com­mence à régress­er. Mais ceci ne veut pas dire que l’épidémie cessera immé­di­ate­ment : la péri­ode d’extinction fera pass­er le nom­bre total de per­son­nes ayant été con­t­a­m­inées depuis le début de l’épidémie à près de 95 % de la pop­u­la­tion. À moins bien sûr qu’existe chez beau­coup de nos conci­toyens l’hypothétique immu­nité naturelle évo­quée plus haut.

Si on estime que le taux de létal­ité (nom­bre de décès / nom­bre total d’infectés) depuis le début de l’épidémie est de l’ordre de 0,5 à 1 % et que l’amélioration de la prise en charge des cas graves va per­me­t­tre de le divis­er par 2, ceci cor­re­spondrait à un total de 100 à 200 000 décès entre le début de l’épidémie et l’atteinte de l’immunité col­lec­tive, suiv­is de 50 à 100 000 pen­dant la péri­ode d’extinction de l’épidémie qui suiv­rait. Une autre con­séquence serait la sub­mer­sion com­plète de notre sys­tème hospitalier.

Ni le gou­verne­ment ni l’opinion publique ne sont prêts à laiss­er délibéré­ment se dévelop­per une telle option basée sur la remon­tée à 3 du coef­fi­cient R.

Une navigation opportuniste permettant d’attendre l’arrivée d’un vaccin et/ou d’un remède

En dehors de l’éventuel mir­a­cle évo­qué plus haut, ceci sem­ble être la seule voie pos­si­ble. Mais elle risque d’être de plus en plus mal accueil­lie par la pop­u­la­tion. Le retour péri­odique de péri­odes de con­fine­ment total ou de restric­tions sévères aura un effet dés­espérant sur l’opinion publique et amèn­era vraisem­blable­ment des réac­tions imprévis­i­bles qui pour­ront être amal­gamées avec d’autres types de mécontentements.

Enfin con­tin­ueront à prospér­er, trans­mis­es par les médias et les réseaux soci­aux, des idées com­plo­tistes chez toute une frange de la pop­u­la­tion influ­encée par des mem­bres du corps médi­cal ayant bien com­pris que des pris­es de posi­tion à con­tre­pied de la doxa offi­cielle étaient la meilleure façon d’accéder à la notoriété.

Tout ceci risque d’entraîner le refus de la vac­ci­na­tion par une part impor­tante de la pop­u­la­tion et d’induire un retard dans la dis­pari­tion de l’épidémie ou même de la ren­dre chronique.

Annexe 1 : Modélisation utilisant Excel

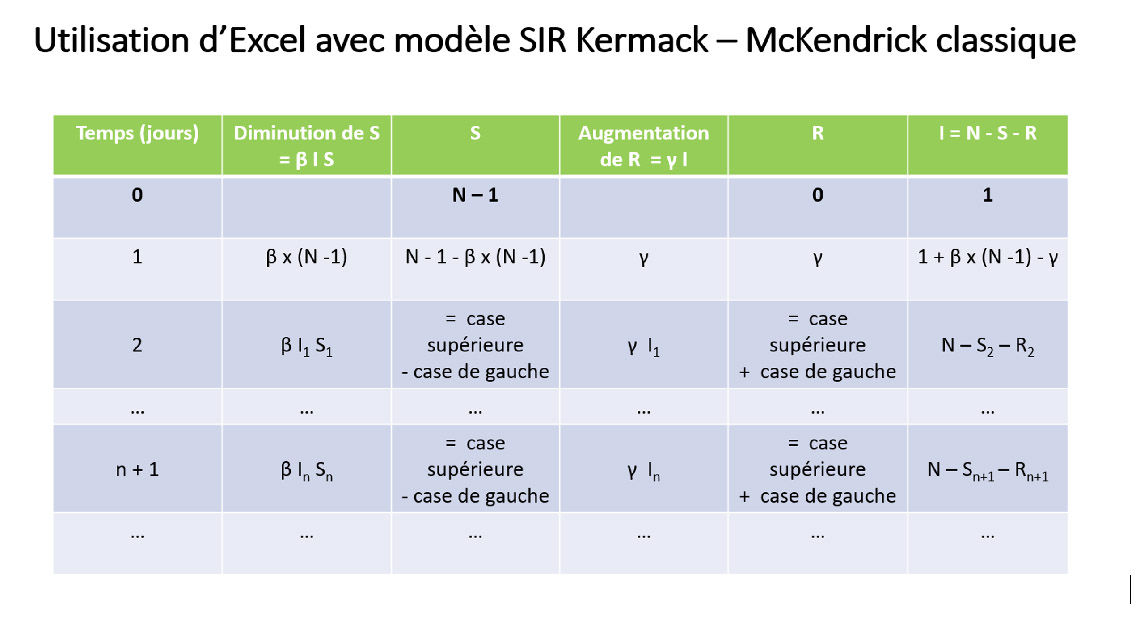
Annexe 2 : Précision sur le taux de contamination de la population apportant une immunité collective (herd immunity)

(cf. l’article « Une mod­éli­sa­tion sim­ple util­isant Excel … » dans la J&R n° 758 d’octobre 2020)

L’emploi d’Excel per­met de déter­min­er facile­ment le taux d’immunité col­lec­tive, c’est-à-dire le pour­cent­age de la pop­u­la­tion qui doit avoir été con­t­a­m­iné (ou vac­ciné, ou éventuelle­ment ne pou­voir devenir con­tagieuse) pour que l’épidémie s’arrête d’elle-même. Il suf­fit de pro­longer le tableau con­tenant S, I et R jusqu’à ce que I atteigne son max­i­mum I_max.

On remar­que que ce taux est très dépen­dant de R. Une série d’essais Excel avec des R allant de 1 à 4 donne la courbe suiv­ante, qui est con­forme avec la for­mule don­née dans les cours d’épidémiologie pour une épidémie à R constant :

Seuil d’immunité col­lec­tive selon le mod­èle SIR de 1927 = 1 – 1/R.

N’est donc pas totale­ment exacte l’affirmation que l’on entend ou lit sou­vent, selon laque­lle pour attein­dre une immu­nité col­lec­tive il faut que le taux total de per­son­nes ayant été infec­tées dépasse 60 ou 70 %. Ceci n’est vrai si on souhaite simul­tané­ment per­me­t­tre à la pop­u­la­tion de retrou­ver exacte­ment le même mode de vie qu’avant l’épidémie (aucune restric­tion aux ren­con­tres, aux déplace­ments, aucun port de masque, pas de gestes-bar­rières, pra­tique uni­verselle des bis­es et des accolades …).

La courbe mon­tre que si une pop­u­la­tion réus­sit à main­tenir de façon durable un R inférieur à 1,5 l’immunité col­lec­tive est obtenue dès que le cumul d’infectés atteint 33 % de la pop­u­la­tion (par exem­ple un peu plus de 20 % pour un R de 1,3). La com­bi­nai­son d’un R et d’un taux cumulé d’infection de la pop­u­la­tion per­me­t­tant de se posi­tion­ner au-dessus de la courbe per­met d’attendre l’arrivée d’un vac­cin, d’un remède ou d’une éventuelle muta­tion favor­able du virus. Cer­taines zones à forte den­sité de pop­u­la­tion sont vraisem­blable­ment en train d’atteindre ce niveau, mais s’y main­tenir de façon durable impose de ne pas laiss­er aug­menter le R qui aura per­mis d’en bénéficier.

À not­er qu’existe à la fin de l’article de la J&R n° 758 « Une mod­éli­sa­tion sim­ple util­isant Excel … » une erreur d’interprétation du terme « immu­nité col­lec­tive » : tra­di­tion­nelle­ment son seuil cor­re­spond à l’atteinte du pic de l’épidémie – nom­bre max­i­mum d’infectés simul­tanés ou I_max –, moment à par­tir duquel l’épidémie com­mence à régress­er. Le sché­ma de l’article du n° 758 rend compte d’un pour­cent­age dif­férent (et plus impor­tant) qui est celui du total de la pop­u­la­tion qui aura été con­t­a­m­iné à la fin de l’épidémie.

Pour­cent­age de la pop­u­la­tion ayant été con­t­a­m­iné en fin d’épidémie en fonc­tion de R

Taux _{I final} = Taux final d’infectés selon le mod­èle SIR de 1927

Taux _{I final} = 1 – exp ( ‑R x Taux _{I final} )

Les deux courbes sont dif­férentes car l’épidémie con­tin­ue après le pic de I_max jusqu’à son extinc­tion totale, et il y a donc encore de nom­breuses infec­tions après l’atteinte du seuil d’immunité collective.

Le e = mc²  de l’épidémiologie

D’après le mod­èle SIR de 1927, dans une pop­u­la­tion non-vac­cinée et sans aucune immu­nité naturelle,

tant que la pro­por­tion d’individus ayant été infec­tés est faible, à l’instant t

le nom­bre d’infectés croît (ou décroît) comme une fonc­tion expo­nen­tielle d’exposant (R‑1) x t / D

R étant le « taux de repro­duc­tion » dif­fusé régulièrement

D la durée moyenne d’infection

Pour les non math­é­mati­ciens : expo­nen­tiel n’est pas sys­té­ma­tique­ment syn­onyme de crois­sance rapide

Si R est plus petit que 1, l’exposant est négatif et le nom­bre d’infectés décroît

Si R est très légère­ment supérieur à 1, l’exposant est très petit et le nom­bre d’infectés croît lentement

---

Articles similaires :

Covid-19 : inter­ro­ga­tions sur le mod­èle épidémi­ologique,
Prise en compte de la vac­ci­na­tion et du « vari­ant anglais » Mod­èles math­é­ma­tiques d’épidémies les plus élaborés : pourquoi leurs prévi­sions ini­tiales sont-elles sou­vent exces­sive­ment pessimistes ? Covid-19 : une mod­éli­sa­tion sim­ple util­isant Excel, acces­si­ble aux non-math­é­mati­ciens et pleine d’enseignements SARS-CoV­‑2 : « Où est caché le loup ? » Covid-19 et impres­sion 3D : une crise peut-elle chang­er le des­tin d’une technologie ? Le cuiv­re, ses alliages et les épidémies