Essai d’analyse des expériences de Maurice Allais sur le pendule paraconique

Dans un livre récent, L’a­ni­so­tro­pie de l’es­pace¹, Mau­rice Allais a racon­té ses tra­vaux des années 1954–1960 et ses déboires qui ont sui­vi. Ayant lu ce livre qui nous a beau­coup trou­blés nous avons déci­dé sinon de refaire les expé­riences du moins de refaire avec des ordi­na­teurs modernes l’a­na­lyse sta­tis­tique qui avait conduit Mau­rice Allais à pen­ser que l’in­fluence de la Lune et du Soleil sur ses pen­dules était cent mil­lions de fois supé­rieure à ce que pré­voyait la théo­rie moderne de la gravitation.

Nous avons donc deman­dé à Mon­sieur Allais ses cahiers de labo­ra­toire qu’il nous a aima­ble­ment four­nis. Les résul­tats se pré­sentent sous la forme de sept séries de mesure de l’a­zi­mut du plan prin­ci­pal d’os­cil­la­tion d’un lourd pendule.

Ces « séries enchaî­nées » sont obte­nues en lâchant le pen­dule à 11 cen­ti­mètres de la ver­ti­cale du sup­port et en le lais­sant oscil­ler pen­dant qua­torze minutes (il ne s’é­carte plus alors qu’à 9 cen­ti­mètres de la ver­ti­cale) puis en rame­nant le pen­dule à 11 cen­ti­mètres dans le plan prin­ci­pal d’os­cil­la­tion final des qua­torze minutes pré­cé­dentes et en le lâchant à nou­veau vingt minutes après le lâcher précédent.

Les six minutes inter­mé­diaires sont néces­saires pour des rai­sons expé­ri­men­tales, en par­ti­cu­lier afin d’ef­fec­tuer le chan­ge­ment de la bille de sup­port du pen­dule (les billes sont sys­té­ma­ti­que­ment chan­gées à chaque expé­rience pour éli­mi­ner tout effet d’u­sure) puis pour assu­rer des lâchers suc­ces­sifs tout à fait neutres.

L’in­té­rêt prin­ci­pal de ces expé­riences est leur durée : envi­ron un mois cha­cune. Par exemple les séries simul­ta­nées de juillet-août 1958, l’une à Saint-Ger­main dans les labo­ra­toires de l’IR­SID et l’autre à Bou­gi­val dans la car­rière du « Blanc Miné­ral » à 57 mètres sous la sur­face du sol, ont com­men­cé le 1^er juillet à 17 heures 40 (TU) et se sont ter­mi­nées à 4 heures TU le 1^er août. Cela repré­sente 2 192 mesures d’a­zi­mut (à 0,1 grade près) et donc 2 191 lâchers successifs.

On pour­rait s’é­ton­ner que les oscil­la­tions des pen­dules ne suivent pas pure­ment et sim­ple­ment la pré­ces­sion de Fou­cault, comme cela se pro­duit d’ailleurs juste après chaque lâcher. Cepen­dant bien­tôt diverses per­tur­ba­tions font que le pen­dule n’os­cille plus dans un plan ver­ti­cal mais selon une ellipse très allon­gée (dont le « plan prin­ci­pal » est le plan ver­ti­cal du grand axe). Cette ellipse subit aus­si la pré­ces­sion d’Ai­ry des pen­dules sphé­riques, ce qui fait que d’une part les expé­riences clas­siques du pen­dule de Fou­cault uti­lisent de très longs pen­dules pour mini­mi­ser les effets per­tur­ba­teurs² et d’autre part les pen­dules d’un peu moins d’un mètre de Mau­rice Allais sont d’ex­cel­lents détec­teurs de ces effets perturbateurs.

Ces effets per­tur­ba­teurs sont si forts pour un pen­dule métrique que son plan prin­ci­pal ne pivote pas per­pé­tuel­le­ment dans le même sens, comme le vou­drait la pré­ces­sion de Fou­cault, et dans les « séries enchaî­nées » de Mau­rice Allais il oscille un mois durant au voi­si­nage de son plan ori­gi­nel de lan­ce­ment lequel est en géné­ral dans l’a­zi­mut 160 ou 170 grades.

Sans donc refaire ces expé­riences nous avons ana­ly­sé les séries numé­riques cor­res­pon­dantes. L’é­quipe de Paul Alba et G. P. a ana­ly­sé les séries 3, 5 et 6 (soit celles de juin-juillet 1955, novembre-décembre 1959 et mars-avril 1960), tan­dis que l’é­quipe Georges Hoy­nant-Chris­tian Mar­chal ana­ly­sait les séries 4, 5 et 7 (les séries 4 et 7 étant les séries simul­ta­nées de Saint-Ger­main et Bou­gi­val pré­sen­tées ci-dessus).

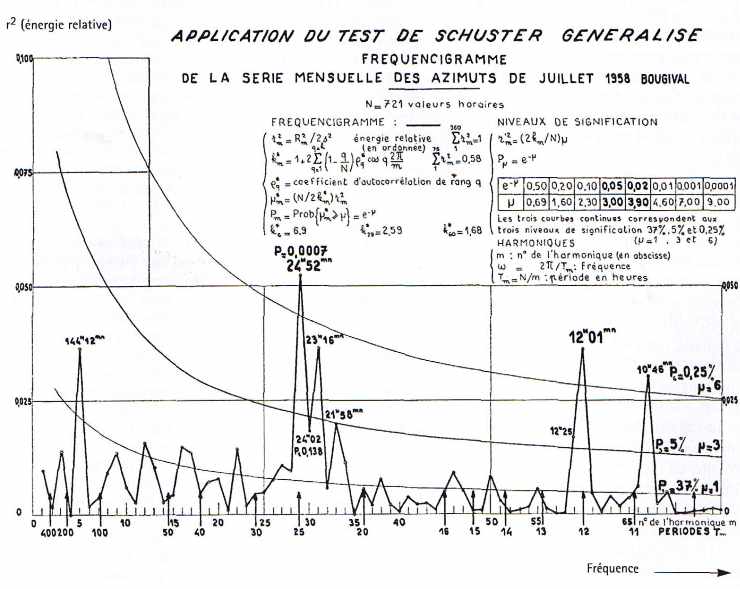
Je dois me faire ici le témoin de l’é­mer­veille­ment de Georges Hoy­nant consta­tant la concor­dance de ses résul­tats, obte­nus par des mil­liards d’o­pé­ra­tions en machine, avec ceux de Mau­rice Allais obte­nus en appli­quant sa méthode « géné­ra­li­sa­tion du test de Schus­ter » avec les moyens numé­riques des années 1955–1960 (cf. figure 1 et note 3).

Cepen­dant nous ne trou­vions aucune cor­ré­la­tion signi­fi­ca­tive entre les séries simul­ta­nées 4 et 7 de Saint-Ger­main et Bou­gi­val, contrai­re­ment à ce qu’é­crit Mau­rice Allais dans son livre. Très ennuyés nous lui expo­sons la situa­tion, mais il nous répond : « faites donc l’é­tude non en fonc­tion du temps mais en fonc­tion de l’angle horaire de la Lune ». Ce der­nier, que nous appel­le­rons L, est par défi­ni­tion nul quand la Lune passe au méri­dien du lieu et croît de 15°, ou une heure, chaque fois que la Lune pro­gresse de 15° vers l’ouest. Cet angle n’est pas une fonc­tion uni­forme du temps et le mou­ve­ment de la Lune a d’im­por­tantes irrégularités.

Cette seconde étude est évi­dem­ment plus com­plexe mais le meilleur ajus­te­ment sinu­soï­dal (moindres car­rés) de cha­cune des deux séries montre une évi­dente parenté :

Pour la série de Saint-Ger­main : Azi­mut ~ 164,2 gr + 0,9 gr sin (L‑150°)

Pour la série de Bou­gi­val : Azi­mut ~ 161,4 gr + 1,2 gr sin (L‑165°)

Ain­si donc l’un des maxi­mums impor­tants du fré­quen­ci­gramme de la figure 1 a une période très voi­sine de 24 heures 50 minutes, période moyenne de l’angle L, les azi­muts des deux séries simul­ta­nées ont mani­fes­te­ment une cor­ré­la­tion signi­fi­ca­tive en fonc­tion de cet angle L et « l’ef­fet lunaire » est maxi­mal quelques heures après le pas­sage de la Lune au méri­dien ou à l’an­ti-méri­dien, exac­te­ment comme pour les marées… Recon­nais­sons qu’il y avait là de quoi être trou­blé ou enthousiasmé !

Figure 1.A.
Fré­quen­ci­gramme de l’expérience de Bou­gi­val obte­nu par la méthode du “ test de Schus­ter géné­ra­li­sé ”.

Cepen­dant les pré­cau­tions d’u­sage, que l’on ne pou­vait guère prendre en 1960 étant don­né la lon­gueur des cal­culs, conduisent à modé­rer cet enthousiasme.

Tout d’a­bord, même si l’on met à part les très rares « grandes excur­sions », l’é­cart-type des résul­tats par rap­port à la droite de régres­sion, soit 3,5 grades envi­ron, est beau­coup plus impor­tant que l’am­pli­tude des réso­nances obser­vées ce qui est évi­dem­ment très défavorable.

Ensuite, et sur­tout, si l’on ana­lyse sépa­ré­ment les deux quin­zaines d’une expé­rience on ne retrouve plus du tout les mêmes réso­nances ce qui n’est pas très éton­nant étant don­né l’im­por­tance du bruit de fond mais est évi­dem­ment très gênant quant à l’interprétation.

Enfin les tests plus com­plexes mais mieux adap­tés que l’a­na­lyse de Fou­rier clas­sique à l’é­tude des phé­no­mènes très brui­tés (test du maxi­mum de vrai­sem­blance ou de Kol­mo­go­rov-Smir­nov, etc.) conduisent eux aus­si à des conclu­sions miti­gées : il y a quelque chose mais on ne sait pas quoi et à ce jour l’on ne peut pas être sûr que la Lune ou le Soleil jouent un rôle impor­tant dans les oscil­la­tions du pen­dule paraconique…

On peut donc conclure que :

1) Mau­rice Allais est un excellent mathé­ma­ti­cien et sta­tis­ti­cien et sa méthode « géné­ra­li­sa­tion du test de Schus­ter« ³ mérite de deve­nir un outil majeur des études statistiques.

2) Les mou­ve­ments du pen­dule para­co­nique ne sont pas du « bruit blanc ». Il y a là des phé­no­mènes encore igno­rés et sans doute très ins­truc­tifs mais dif­fi­ciles à analyser.

3) Il convien­drait donc de refaire cette série d’ex­pé­riences dans les meilleures condi­tions pos­sibles. Tout d’a­bord en éli­mi­nant au maxi­mum l’a­ni­so­tro­pie du sup­port, ce qui amoin­dri­ra gran­de­ment une source de bruits nui­sibles, ensuite en exa­mi­nant si le sup­port par l’in­ter­mé­diaire d’une bille sphé­rique est bien le meilleur : les sphères sont sou­vent en fait des poly­èdres à un grand nombre de faces, sur­tout si la struc­ture est cris­tal­line, et le contact sphère-plan donne des défor­ma­tions impor­tantes et variables. Sans doute une cuvette en saphir avec une pointe en acier don­ne­rait de meilleurs résultats.

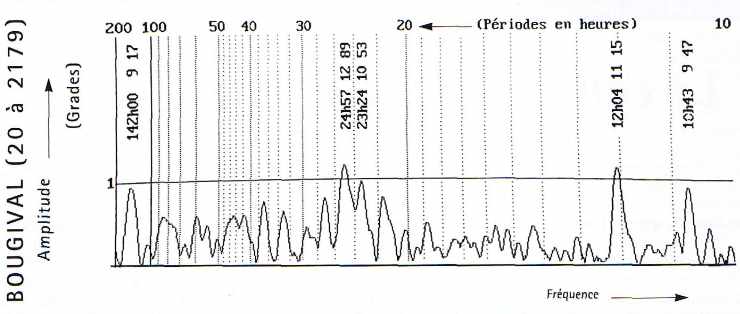
Figure 1.B.
Le même fré­quen­ci­gramme (don­nant l’amplitude au lieu de l’énergie) obte­nu par une méthode sta­tis­tique actuelle. L’amplitude est pro­por­tion­nelle à la racine car­rée de l’énergie.

Il fau­dra aus­si bien sûr faire les longs, oné­reux et dif­fi­ciles mais néces­saires essais de fidé­li­té et de répé­ta­bi­li­té avec deux ou plu­sieurs pen­dules iden­tiques à quelques déca­mètres les uns des autres, essais faute des­quels on risque tou­jours de ne « mesu­rer que la tem­pé­ra­ture » ou toute autre variable analogue.

Enfin les méthodes modernes d’en­re­gis­tre­ment auto­ma­tique et peut être aus­si la pos­si­bi­li­té d’ef­fec­tuer l’ex­pé­rience sous pres­sion réduite, pour dimi­nuer l’ar­mor­tis­se­ment, devraient pou­voir sim­pli­fier consi­dé­ra­ble­ment la tâche à accomplir.

Il serait très inté­res­sant qu’une étude post-doc­to­rale voire une thèse soit entre­prise sur le sujet géné­ral des pen­dules courts, sujet cer­tai­ne­ment très riche et très instructif.

________________________________
1. Mau­rice Allais. L’a­ni­so­tro­pie de l’es­pace – 1. Les don­nées de l’ex­pé­rience. Clé­ment Juglar édi­teur, 1997.
2. Alain Mar­vil­liers. « L’ex­pé­rience du pen­dule de Fou­cault » Revue du Palais de la Décou­verte. Vol 26, n° 258 pages 30–45. Mai 1998.
3. Mau­rice Allais. « Test de pério­di­ci­té. Géné­ra­li­sa­tion du test de Schus­ter au cas des séries tem­po­relles auto­cor­ré­lées, dans l’hy­po­thèse d’un pro­ces­sus de per­tur­ba­tions aléa­toires d’un sys­tème stable ». Bul­le­tin de l’Ins­ti­tut Inter­na­tio­nal de Sta­tis­tique, 33^e ses­sion, pages 1–35. Paris, 1961.

---

Articles similaires :

Fron­tin, un ingé­nieur au pre­mier siècle (après Jésus-Christ) ? Cais­sier de la pro­mo 42–43 24 sep­tembre 1904 Le Prin­cipe de Rela­ti­vi­té d’Henri Poin­ca­ré (1854−1912) Un antique oublié : Eugène VERLANT (1867−1958) Éga­li­té des chances ou égalitarisme