Étymologie :
À propos des mathématiques

Le nom des mathématiques vient du grec.
La notion de mathématiques en grec
Le mot mathêmatikos appartient à la famille du verbe grec manthanein, signifiant d’abord « apprendre par l’expérience, apprendre à faire », puis sans plus de précision, « étudier, apprendre », d’où aussi « comprendre ». Ce verbe avait donc un sens très général, tout comme les mots mathos « connaissance » (d’où amathês « ignorant » et polumathês « très savant, polymathe »), mathêsis « apprentissage », mathêma, atos « discipline enseignée, science », au pluriel, mathêmata, d’où enfin mathêmatikos « qui s’adonne à l’étude ».
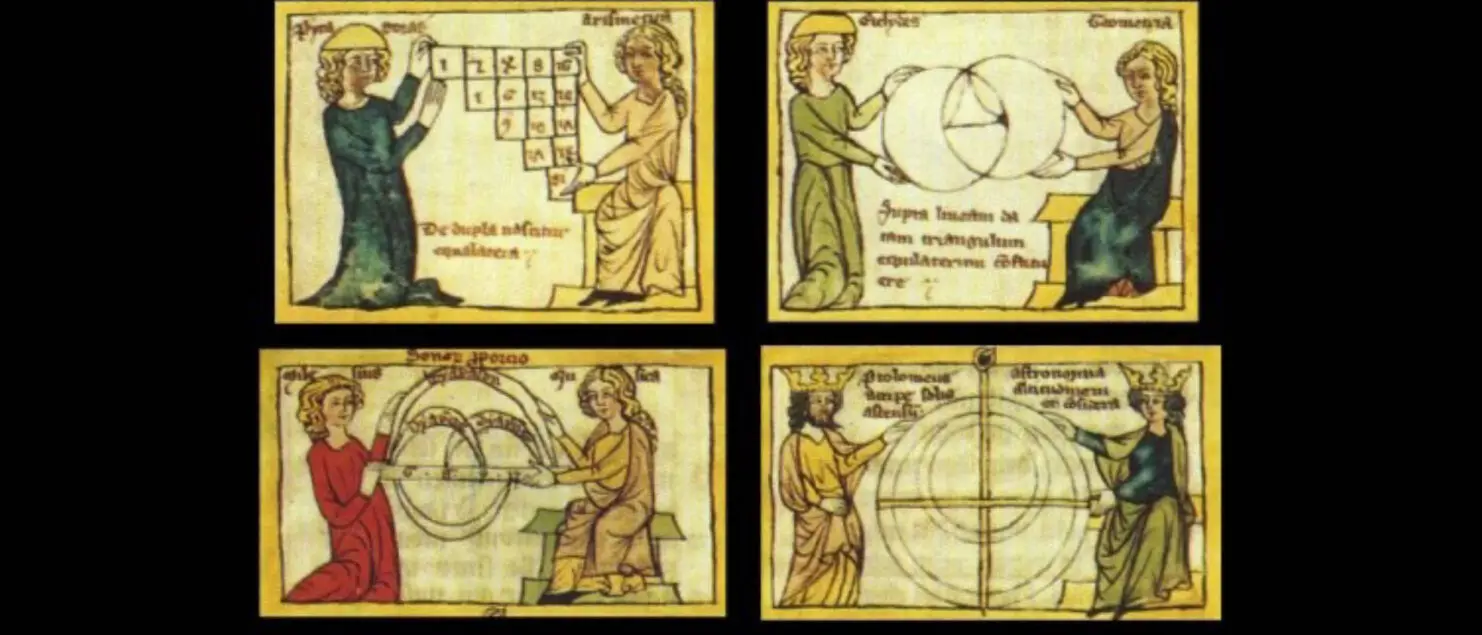
Cependant, mathêmata, mathêmatikos prennent un sens plus restreint chez les philosophes classiques. Ainsi, Platon dans les Lois associe « trois disciplines », en grec tria mathêmata : celle « des nombres et du calcul », « celle qui mesure la longueur, la surface et la profondeur » et « celle qui nous instruit des révolutions des astres », c’est-à-dire l’arithmétique, la géométrie et l’astronomie. Il rappelle d’autre part dans la République que « l’astronomie et la musique sont sœurs, comme disent les Pythagoriciens », qui considéraient en effet ces quatre disciplines, de l’arithmétique à la musique, comme un tout.
Plus tard, dans la Physique, Aristote écrit à propos des scientifiques qu’il nomme mathêmatikos et phusikos : « Il convient d’examiner par quoi le mathématicien se distingue du physicien ; en effet appartiennent aux corps physiques les surfaces, solides, grandeurs et points qui font l’objet des études mathématiques. » Ainsi Aristote restreint le terme général mathêmatikos au sens de celui dont les études permettent d’expliquer les phénomènes physiques, ce qui est encore aujourd’hui la première finalité des mathématiques.
La musique et l’astronomie dans les mathématiques
Le son émis par une corde vibrante fait le lien entre musique et mathématiques. Ainsi, Pythagore montrait qu’une corde deux fois plus courte qu’une autre émet la même note mais une octave au-dessus, et que si les longueurs de deux cordes sont dans un rapport de nombres entiers, alors les sons émis sont en harmonie (du grec harmonia « ajustement, harmonie » lié à la racine indo-européenne *ar- « joindre, adapter », cf. ÉtymologiX d’avril 2018). Cette observation est à la base de la construction d’une gamme musicale, et inversement cela explique les termes mathématiques de division harmonique d’un segment, ou de moyenne harmonique de deux grandeurs. En outre les 7 notes de musique étaient reliées aux orbites des 7 astres « errants » selon l’harmonie des sphères de Pythagore. Ce rôle de la musique et de l’astronomie s’est affirmé dans la mathématique médiévale, et le philosophe Boèce instaurait au début du VIe siècle le quadrivium : l’arithmétique, la musique, la géométrie et l’astronomie, les quatre composantes de la mathématique, puis des mathématiques à partir du XVIIe siècle. Le Principia mathematica (1687 à 1726) de Newton est bien un monument de l’astronomie autant que des mathématiques, et Newton associait par ailleurs les 7 couleurs de l’arc-en-ciel aux 7 notes de musique. Le dictionnaire de l’Académie incluait encore la musique dans les mathématiques jusqu’à sa 5e édition (1798), ainsi que l’astronomie jusqu’à sa 7e édition (1878).
Épilogue
Les mathématiques, maintenant séparées de la musique et de l’astronomie, ont retrouvé une structure quaternaire avec l’analyse et les probabilités, venues compléter l’algèbre (issue de l’arithmétique) et la géométrie.