Histoire de l’enseignement de la mécanique à l’École polytechnique

Présent depuis la création de l’École polytechnique, l’enseignement de la mécanique s’y est longtemps tenu en équilibre instable entre vérités mathématiques et utilités des machines, théorisation et expérimentation physique. La place de la mécanique dans l’histoire de l’X témoigne ainsi de l’identité spécifique d’une école à l’interface
entre industrie, ingénierie et recherche.
À la fondation de l’X en 1794, l’analyse mathématique et la mécanique sont confiées au même « instituteur », Joseph Louis Lagrange. Joseph Fourier, comme instituteur adjoint, s’il démontre le théorème des puissances virtuelles dans le cadre du programme théorique de Lagrange, le fait pour le cours d’analyse de Gaspard de Prony, un ingénieur des Ponts qui tient au concret. Les deux disciplines sont temporairement attribuées à des enseignants différents, de 1799 à 1816, avant d’être à nouveau regroupées dans les cours d’André-Marie Ampère et Augustin Louis Cauchy (1805). Dans les années 1830, l’enseignement de la mécanique est critiqué pour sa mathématisation excessive qui, pour d’anciens professeurs de mécanique comme Siméon Denis Poisson (1798), rend les élèves incapables de passer de la théorie aux applications. À partir de 1850, il est rapproché d’enseignements plus appliqués tels que le cours de machines et influencé par le modèle de la physique expérimentale.
REPÈRES
Dès 1794, la mécanique participe du projet de créer un enseignement scientifique pluridisciplinaire fondé sur l’attribution d’un rôle prédominant aux sciences mathématiques. Selon le plan conçu par Gaspard Monge, l’instruction des mathématiques se subdivise en deux branches principales : la géométrie, ou étude des formes, avec ses applications à la stéréotomie, l’architecture ou les fortifications, et l’analyse, ou étude du mouvement, très orientée vers des applications à la mécanique, conçue comme science de l’équilibre, l’hydrostatique ou la théorie des machines.
Mais la proximité entre mécanique et analyse perdurera encore plusieurs décennies. Au tournant des XIXe et XXe siècles, des fonctions de répétiteur ou professeur de mécanique sont ainsi occupées par des mathématiciens tels que Charles Ange Laisant (1859) ou Paul Appell. Il n’est d’ailleurs pas rare qu’un enseignant passe d’un domaine à l’autre. Par exemple, Jean Marie Constant Duhamel (1814) remplace provisoirement en 1830 Gustave Gaspard Coriolis (1808) au poste de répétiteur d’analyse et de mécanique, avant d’être nommé répétiteur d’analyse appliquée en 1831, puis de remplacer en 1836 Henri Navier (1802) à la chaire de mécanique. Encore en 1883, Émile Sarrau (1857) est nommé professeur de mécanique après avoir officié comme répétiteur d’analyse…
L’esprit analytique dans l’approche de la mécanique
Malgré sa cohérence, le plan d’étude de Monge est remis en cause dès 1795 avec la création du système des écoles d’application qui incite l’École à se concentrer sur une formation généraliste. Cette réorganisation donne une place croissante à l’analyse, donc à la mécanique, qui, à défaut d’être aussi directement applicable que la géométrie de Monge, est susceptible d’une plus grande diversité d’applications du fait de son caractère plus abstrait. Le « plus haut point de vue » d’un enseignement fondamental doit désormais précéder les applications. Cela vaut même pour la notion de travail en mécanique issue des travaux de Lazare Carnot.
Cette nouvelle conception doit beaucoup à l’influence de l’un des grands mathématiciens et mécaniciens de l’époque, Pierre Simon Laplace. Nommé examinateur en 1795, ce dernier exerce un grand pouvoir sur l’École en contrôlant les exigences des concours d’entrée et de sortie. Surtout, Laplace allie prestige académique et pouvoir politique : brièvement ministre de l’Intérieur – alors tutelle de Polytechnique – sous le Consulat, puis sénateur, il met en place le conseil de perfectionnement en 1799 pour opérer la jonction entre les corps, l’Académie des sciences et l’École polytechnique, soit entre l’industrie, l’ingénierie et la recherche. Pour les cours d’analyse et de mécanique, la volonté est de toujours être à la pointe. Cauchy, dont le cours d’analyse de 1821 recèlera les dernières prouesses analytiques, obtiendra son poste pour cette raison précise.
Fourier remplace Lagrange
Si l’esprit analytique règne alors, avec le traitement des équations, le jeu sur les fonctions, etc., il ne faudrait pas donner une image idyllique de ce renouveau mathématique. Lagrange entend formaliser le calcul différentiel et intégral à partir d’une conception algébrique mais ne permet pas l’accès à tous les outils qu’attendent les applications à la mécanique. Les notes de cours prises en 1797 par Jean Legentil (1795), étudiées récemment par Adrien Dufour (2011) et Stéphane Horte (2011) dans le cadre de l’enseignement d’histoire des sciences proposé par le département HSS, témoignent de ce que les cours réellement dispensés par Lagrange sont bien moins théoriques que leur publication dans la Théorie des fonctions analytiques de 1797.
Chaque leçon est associée à un problème précis, le mouvement d’un projectile dans un milieu résistant permettant par exemple d’introduire des propriétés complexes d’analyse et d’addition des forces. Mais rien n’y fait : le cours de Lagrange ne passe pas. Son adjoint Fourier est alors chargé de produire un cours de remplacement.
“La mécanique irrigue en profondeur l’analyse mathématique.”
La structuration de l’enseignement de l’analyse
Les cours de l’X sont la première véritable structuration de l’enseignement de l’analyse, branche des mathématiques développée au XVIIIe siècle avec l’essor de la mécanique newtonienne. Le calcul différentiel est au cœur de la théorie de Newton : il sert à en énoncer les lois et permet d’en prouver l’efficacité pour mathématiser les mouvements des corps, en astronomie comme en artillerie ou dans la théorie des machines de l’industrie émergente. L’inauguration de ce cours pose donc le défi d’enseigner une science récente, en pleine évolution, qui n’était jusqu’alors maîtrisée que par les savants les plus avancés.
Ce défi pédagogique amène à repenser les fondements de l’analyse. Il fait naître de nouveaux idéaux de rigueur afin de présenter aux élèves des cours fondés sur des notions précises par opposition à certains concepts controversés, comme les « infiniment petits ». De 1794 à 1830, le cours d’analyse fournit l’un des premiers exemples d’enseignement étroitement associé à la recherche d’une solide architecture permettant de constituer une discipline. Moins de trente ans après Lagrange, Cauchy refonde l’analyse sur le concept de limites et de fonctions continues, tout comme aujourd’hui.
Autonomie des mathématiques et de la mécanique
Cette structuration de l’analyse joue un rôle important dans l’autonomisation réciproque des mathématiques et de la mécanique. Il n’est notamment plus question de recourir à des conceptions mécaniques du mouvement, telles que les fluxions de Newton, pour envisager la continuité ou les variations. Mais, à y regarder de plus près, la mécanique irrigue en profondeur l’analyse mathématique. Dans son cours de géométrie analytique, Cauchy propose ainsi de déterminer les axes principaux des coniques et quadriques selon la méthode élaborée par Lagrange pour caractériser la stabilité mécanique des petites oscillations d’un système de corps.
Cette méthode avait notamment été utilisée par Laplace pour démontrer la stabilité du système du monde, c’est-à-dire des oscillations non périodiques des orbites des planètes du système solaire. Elle consiste à linéariser le problème en le mathématisant par un système d’équations différentielles linéaires à coefficients constants dont Lagrange détermine les oscillations propres (nous dirions aujourd’hui valeurs propres).
Analyse et mécanique
La même méthode fonctionne pour les surfaces du second degré en raison de la nature quadratique des deux problèmes, mécaniques et géométrique, qui impliquent de diagonaliser une matrice symétrique. Mais, bien avant la formalisation de l’algèbre linéaire, c’est l’analogie mécanique qui inspire Cauchy. La possibilité d’envisager les oscillations d’un nombre quelconque n de corps lui permet d’explorer la géométrie à n dimensions… puis d’appliquer en retour ses méthodes géométriques à la mécanique : ellipsoïdes de pression en théorie de l’élasticité, petites oscillations de « particules lumineuses »…
Cette intimité polytechnicienne entre analyse et mécanique se retrouvera encore beaucoup plus tard chez Henri Poincaré (1873), aussi bien dans le rôle joué par les cônes de lumière dans son approche de la relativité que dans sa stratégie de linéarisation du problème des trois corps en mécanique céleste, qui reprend la méthode des petites oscillations de Lagrange mais cette fois pour faire osciller le système différentiel lui-même.
La roue hydraulique de Poncelet
Dans le cadre de leur enseignement d’histoire des sciences, Laurent Guin (2011) et Leonel Pauro Velásquez (2011) ont étudié la roue hydraulique à aubes courbes conçue par Poncelet en 1823 dans le cadre d’une mission d’amélioration d’une forge à puissance hydraulique à l’arsenal de Metz. Cette « roue de Poncelet » offre des rendements doubles de ceux des roues à aubes planes alors utilisées. Sa conception est fondée sur le principe des « forces vives », principal concept de la théorie des machines : un « bilan de force vive », c’est-à-dire de l’énergie entre le point où l’eau entre dans la roue et le point d’où elle en sort, permet à Poncelet de mathématiser le travail utile récupérable par une expression différentielle dépendant de deux paramètres, l’angle d’attaque du fluide sur la planchette, d’une part, l’angle d’orientation de la planchette par rapport à la direction de translation d’autre part.
Optimiser le travail utile revient alors à minimiser ces deux angles : il faut donc s’approcher d’une attaque tangentielle de l’eau sur les aubes et d’une grande inclinaison des aubes par rapport aux rayons. D’où l’idée de construire des roues à aubes courbes inclinées. Contrairement à la turbine d’Euler restée au stade de prototype, ces roues seront largement exploitées en France à partir de 1827. Le modèle mathématique de Poncelet sera néanmoins critiqué par Coriolis dès 1829 pour avoir ignoré les turbulences engendrées par l’écoulement de l’eau dans le canal.
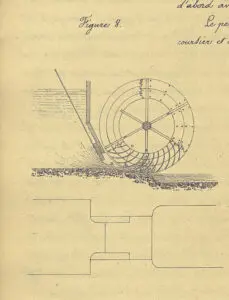
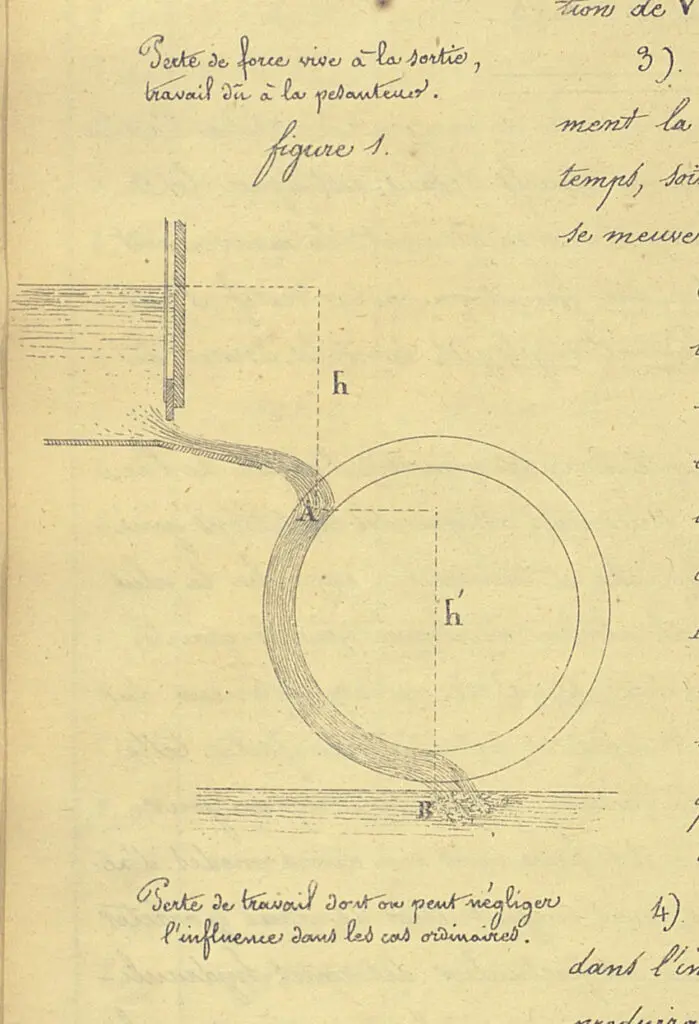
et du génie, 1838.

postérieur à 1846.
L’autonomisation de la mécanique
En 1850, une commission interministérielle abritant en son sein des noms illustres de la mécanique céleste, tel Urbain Le Verrier (1833), comme de la mécanique appliquée, tel Jean Victor Poncelet (1807), promeut un enseignement de la mécanique davantage empirique et utile. Un objectif majeur est de faire bénéficier l’enseignement des machines du pouvoir unificateur de la théorie. La prolifération de dispositifs mécaniques qui accompagne l’industrialisation européenne rend en effet obsolète l’approche descriptive des machines qui avait été développée depuis 1794 par l’usage du dessin géométrique. Sur le plan théorique, le cours de Jean Baptiste Belanger (1808) donne ainsi à partir de 1851 la primauté à la cinématique au détriment de la statique qui, depuis Lagrange, Prony ou Louis Poinsot (1794), constituait le fondement de l’enseignement de la mécanique, jusqu’alors conçue comme science de l’équilibre.
L’évolution des principes de la mécanique rationnelle en tant que discipline est alors marquée par son articulation avec la physique, modèle de science expérimentale alternatif à celui des mathématiques. Cette évolution a fait l’objet de plusieurs travaux de recherche d’élèves. Emmanuel Orsini (2012) a ainsi étudié la place attribuée au concept d’éther – longtemps conçu comme un milieu élastique dont les vibrations expliquaient la théorie de la lumière – bien après l’expérience de Michelson-Morley de 1887, jusque dans les dernières éditions des cours de Painlevé et Léon Lecornu (1872) en 1926–1927. Olivier Gauthé (2011), Xavier Bonnetain (2011), Yoann Desmouceaux (2011) et Sébastien Geeraert (2011) ont, quant à eux, étudié l’émergence de l’enseignement de la mécanique quantique à l’École polytechnique à partir de 1938 au sein des cours de physique de Louis Leprince-Ringuet (1920N) et André Léauté (1902).
Entre pratique et théorie : le dessin
La création de l’École polytechnique s’est accompagnée de l’idéal de concevoir une nouvelle méthode d’enseignement visant à favoriser l’activité des élèves qui « doivent non seulement comprendre, mais exécuter avec précision ». Des laboratoires sont établis pour l’enseignement de la chimie, ainsi que des collections d’instruments pour celui de la physique. La mécanique se trouvant du côté des mathématiques, l’activité des élèves n’y est pas initialement promue par l’expérimentation mais par l’exécution de travaux graphiques à l’aide de modèles. La pratique du dessin géométrique occupe longtemps une place considérable dans l’emploi du temps des élèves et les problèmes mécaniques y jouent un rôle essentiel.
Par exemple, les trajectoires des points de contact de deux engrenages engendrent des courbes à double courbure dont l’étude gagne à combiner calcul différentiel et dessin géométrique. Il s’agit non seulement de décrire des machines – compétences dont un certain nombre de polytechniciens feront usage pour espionner l’industrie britannique – mais aussi de concevoir des innovations mécaniques.
La mécanique dans les collections d’instruments de l’École polytechnique
Probable conséquence de sa proximité avec les mathématiques, la mécanique est longtemps restée absente des collections d’instruments scientifiques anciens de l’École : si de nombreux instruments sont fondés sur des dispositifs mécaniques, rares sont ceux qui ont été conçus pour l’enseignement de la mécanique en tant que tel. Ce n’est que très récemment, à l’occasion de l’inauguration du Mus’X en juin 2018, que le TreX de mécanique a versé à la bibliothèque un ensemble d’instruments ayant servi à l’enseignement expérimental de la mécanique au XXe siècle. Parmi cette collection du TreX de mécanique, citons l’herpolhodographe conçu par Gaston Darboux et Gabriel Koenigs et présenté à l’Exposition universelle de Paris de 1900. Cet instrument permet de tracer des herpolhodies ou courbes engendrées par le mouvement à la Poinsot d’un corps en rotation sur un plan fixe. L’usage de tels instruments pour l’enseignement de la mécanique au XXe siècle reste encore trop peu connu et appelle de nouveaux travaux de recherche dans les collections historiques : avis aux volontaires, parmi les élèves comme parmi les anciens !
Ressources
Konstantinos Chatzis, « Mécanique rationnelle et mécanique des machines à l’École polytechnique, 1800–1860 », dans Amy Dahan Dalmedico, Bruno Belhoste et Antoine Picon (éd.), La formation polytechnicienne : 1794–1994, Paris, Dunod, 1994, p. 95–108.







2 Commentaires
Ajouter un commentaire
Bonjour Monsieur, J’ai lu avec beaucoup d’intérêt votre article. Je ne suis pas particulièrement un mécanicien ou un mathématicien puisque après l’X je suis entré au CNRS puis dans un centre de recherche pharmaceutique. Mais une question qui m’avait tracassé jadis est revenue à mon esprit récemment : Comment arrive-t-on à (ou aux) l’équation de Lagrange ? Le Force = masse X accélération de Newton me semble correspondre assez naturellement à notre intuition : en langage ordinaire si on pousse sur un objet d’une certaine masse de plus en plus fort, il prendra de plus en plus de la vitesse, donc pourquoi ne pas essayer la formulation Force = masse X accélération ? Quand j’étais élève j’avais acheté un livre intitulé Mécanique de Lando et Lifschitz, et je l’ai repris récemment : ils établissent cette équation pour un point matériel en mouvement sous l’effet de forces en appliquant le principe de moindre action, qui dit que l’action entre deux points de la trajectoire est extrêmale ; très bien, mais pourquoi faut-il croire ça, comment a‑t-on l’intuition que cette idée d’extrémum pourrait être une bonne idée ? personnellement je ne sens pas ça ; mon sens physique ne sent pas ça. J’ai cherché des articles sur le web (anglais ou français) mais nulle part je n’ai trouvé ce que je cherche. Pour l’instant ce principe de moindre action et l’usage qu’on en fait qui conduit à l’équation de Lagrange me semble comme un dogme ; ça me rappelle la réponse d’un ami professeur à L’université de Bordeaux à qui je demandais un jour « comment introduis-tu l’équation de Schroedinger H.Psi = E.Psi à tes élèves ?”, sa réponse fut « je leur dis que c’est comme ça ». Si vous avez une bonne lecture merci de me communiquer la référence. Très cordialement.
Cher camarade,
merci pour cette réaction. De fait, la question de la relation entre intuition et formulation d’une théorie est passionnante. Et que dire alors du caractère « intuitif » de la mécanique vue par la relativité générale, toute de géométrie ? Et je ne parle même pas de la « mécanique » quantique … J’ai transmis ta question aux auteurs pour qu’ils te répondent avec compétence.
Robert Ranquet
Rédacteur en chef