Investissements stratégiques en environnement incertain : approche pire-cas

I. Approches actuelles pour l’évaluation du risque

Analyses probabilistes des investissements

I. Approches actuelles pour l’évaluation du risque

Analyses probabilistes des investissements

La plu­part des inves­tis­se­ments indus­triels ou finan­ciers sont géné­ra­le­ment déci­dés en fonc­tion de la valeur actuelle des cash-flows futurs. La théo­rie sou­vent uti­li­sée dans ce cas est le Capi­tal Asset Pri­cing Model, base de la finance moderne et notam­ment décrite dans l’ou­vrage de réfé­rence de Brea­ley et Myers. La valeur uti­li­sée pour chaque cash-flow futur est alors une moyenne (l’es­pé­rance mathé­ma­tique), le risque spé­ci­fique (ou vola­ti­li­té) asso­cié à l’o­pé­ra­tion étant pris en compte par le taux d’actualisation.

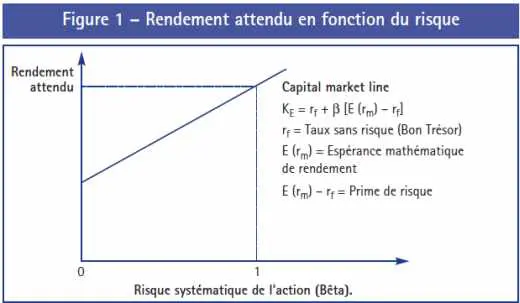
Le CAPM fait le lien entre le retour atten­du d’un inves­tis­se­ment et le risque lié à cet inves­tis­se­ment (voir figure 1). Il sup­pose que les inves­tis­seurs, sur les mar­chés finan­ciers ou au sein de l’en­tre­prise, pour­suivent un double objec­tif : aug­men­ter le retour atten­du et réduire la vola­ti­li­té. Il sup­pose aus­si que l’in­ves­tis­seur rai­sonne sur la moyenne en pra­ti­quant une poli­tique de diver­si­fi­ca­tion active.

Le prin­ci­pal avan­tage de cette approche est sa sim­pli­ci­té d’u­ti­li­sa­tion. Cepen­dant elle est insuf­fi­sante sur un pro­jet d’im­por­tance stra­té­gique pour l’en­tre­prise où rai­son­ner sur la moyenne n’a pas de sens et où le pire- cas peut s’a­vé­rer catastrophique.

Analyse de sensibilité par scénarios

Pour sor­tir d’un rai­son­ne­ment sur la moyenne, une approche cou­rante consiste à étu­dier quelques scé­na­rios pos­sibles, cor­res­pon­dant à des valeurs opti­mistes et pes­si­mistes des para­mètres sus­cep­tibles de varier. L’im­pact de ceux-ci sur le retour atten­du est ain­si étu­dié au cas par cas, condui­sant à une ana­lyse de sen­si­bi­li­té, géné­ra­le­ment avec un modèle simple sur une feuille de calcul.

Cette approche ne per­met pas d’é­tu­dier un grand nombre de scé­na­rios, à cause de la com­bi­na­toire qui en résulte. En consé­quence, elle peut dif­fi­ci­le­ment s’a­dap­ter à un contexte dyna­mique, où des cor­ré­la­tions fortes et com­plexes peuvent exis­ter entre des para­mètres incer­tains sus­cep­tibles de varier au cours du temps.

Méthodes de Monte-Carlo

Lorsque la ges­tion par scé­na­rios est impos­sible à effec­tuer de façon exhaus­tive, même avec des ordi­na­teurs très puis­sants, la méthode rete­nue consiste le plus sou­vent à effec­tuer des tirages au sort avec des lois de pro­ba­bi­li­té fixées à l’a­vance, et à éva­luer les moyennes et les pro­ba­bi­li­tés asso­ciées aux résul­tats(1). Le recours à l’é­va­lua­tion sta­tis­tique per­met de réduire sub­stan­tiel­le­ment le nombre total de cal­culs néces­saires, mais l’en­semble des com­bi­nai­sons à explo­rer pour un résul­tat satis­fai­sant est néan­moins très impor­tant. Dans beau­coup de cas pra­tiques, ce fac­teur rend la méthode inapplicable.

Gestion du risque par externalisation

Face à une situa­tion sin­gu­lière et stra­té­gique pour l’en­tre­prise, mais qui se retrouve sous des formes simi­laires dans d’autres entre­prises, il est par­fois pos­sible d’ex­ter­na­li­ser le risque par assu­rance ou option. Dans ce cas, c’est la socié­té d’as­su­rance ou l’in­ter­mé­diaire finan­cier qui uti­lise les méthodes pro­ba­bi­listes décrites pré­cé­dem­ment pour éta­blir le prix de l’assurance.

La ges­tion par exter­na­li­sa­tion est un ins­tru­ment simple à mettre en œuvre, et qui apporte des garan­ties de résultats.

Limites des approches actuelles

Les approches décrites ci-des­sus, cou­ram­ment uti­li­sées, ont cepen­dant cer­taines limites :

• le CAPM ne four­nit qu’un résul­tat pro­ba­bi­liste, qui est sou­vent de peu d’in­té­rêt dans un contexte stra­té­gique où le pire-cas doit être connu ;
• l’ap­proche par scé­na­rio sur feuille de cal­cul ne per­met pas de tenir compte d’in­te­rac­tions com­plexes et dyna­miques, et d’in­cer­ti­tudes sus­cep­tibles de varier dans le temps ;
  . l’ap­proche Monte-Car­lo a une com­plexi­té qui croît très for­te­ment avec la « taille » du pro­blème, ce qui limite l’ho­ri­zon tem­po­rel sur lequel peut por­ter l’analyse ;
• l’ex­ter­na­li­sa­tion n’est pos­sible que si un mar­ché du risque existe.

Ces limites et les évé­ne­ments récents sur les mar­chés finan­ciers montrent l’in­té­rêt de tenir compte du pire-cas dans un contexte fon­da­men­ta­le­ment dyna­mique et incertain.

2. Modélisation par les systèmes dynamiques

La dynamique des systèmes

La dyna­mique des sys­tèmes est une dis­ci­pline des mathé­ma­tiques appli­quées qui a récem­ment pris une grande ampleur grâce aux capa­ci­tés de simu­la­tion des ordi­na­teurs. Elle est à la base de nom­breuses approches de pré­dic­tion par exemple en météo­ro­lo­gie, méca­nique des struc­tures… Elle a été pro­mue dans le domaine de l’é­co­no­mie notam­ment par Jay W. For­res­ter du MIT. Appli­quée à notre pro­blème, elle per­met de prendre en compte la com­plexi­té et de se pro­je­ter dans le temps en tenant compte des boucles, cor­ré­la­tions et diverses rétro­ac­tions entre les dif­fé­rentes com­po­santes du système.

Limites de la modélisation dynamique

La modé­li­sa­tion par sys­tèmes dyna­miques prend en compte la dyna­mique ain­si que la com­plexi­té d’un sys­tème, remé­diant ain­si à cer­taines limites des approches clas­siques. Cepen­dant, cette modé­li­sa­tion ne prend pas en compte l’in­cer­ti­tude liée au sys­tème. On peut bien sûr uti­li­ser la simu­la­tion pour tes­ter les scé­na­rios. On retrouve alors le pro­blème de l’ex­plo­sion com­bi­na­toire ren­con­trée aupa­ra­vant dans les approches de type Monte-Carlo.

De ce constat est né le pro­jet de col­la­bo­ra­tion entre L. El Ghaoui et A.T. Kear­ney pour éva­luer la per­ti­nence de cou­pler « modé­li­sa­tion par sys­tème dyna­mique » avec une nou­velle approche mathé­ma­tique « l’a­na­lyse pire-cas » pour aider à la déci­sion stra­té­gique en envi­ron­ne­ment incertain.

3. Analyse pire-cas et aide à la décision stratégique

Analyse pire-cas et garantie sur le résultat

L’a­na­lyse pire-cas est une tech­nique récente per­met­tant d’ap­por­ter des garan­ties sur un résul­tat en envi­ron­ne­ment incer­tain. Elle répond à des ques­tions telles que : « quelles sont les valeurs mini­males et maxi­males que peuvent prendre des fonc­tions dont les para­mètres ne sont connus qu’à un inter­valle près ? ».

L’a­na­lyse pire-cas est aujourd’­hui cou­ram­ment uti­li­sée dans un contexte d’in­gé­nie­rie des sys­tèmes dyna­miques : pilo­tage de cen­trale nucléaire mal­gré des pannes de cap­teurs, détec­tion de col­li­sion de tra­fic aérien, éla­bo­ra­tion de poso­lo­gie opti­male pour le trai­te­ment d’in­fec­tions, etc. Dans toutes ces appli­ca­tions, il est cru­cial d’a­voir la capa­ci­té de trai­ter des incer­ti­tudes éven­tuel­le­ment grandes, et d’ap­por­ter des garan­ties sur le résultat.

Le cal­cul n’est pas com­bi­na­toire car il est for­mu­lé comme un pro­blème de pro­gram­ma­tion mathé­ma­tique convexe, que l’on sait résoudre effi­ca­ce­ment en un temps réduit. Il en résulte des inter­valles de confiance qui ne sont pas stric­te­ment opti­maux, mais qui offrent un excellent com­pro­mis entre le temps de cal­cul néces­saire et la pré­ci­sion obtenue.

Application aux investissements stratégiques

EXEMPLES DE CAS D’APPLICATION DE L’APPROCHE PIRE-CAS

1. Stra­té­gie d’un nou­vel entrant sur un sec­teur com­plexe et déré­gu­lé (Télé­coms, éner­gie, transport…).
    
2. Tac­tiques de pri­cing en envi­ron­ne­ment dyna­mique (Télé­com­mu­ni­ca­tions mobiles, trans­port aérien…).
    
3. Déci­sion d’in­ves­tis­se­ment sur un nou­veau pro­duit (auto­mo­bile, pharmacie…).
    
4. Acqui­si­tions et joint-ventures.

Pour un inves­tis­se­ment stra­té­gique, on peut cou­pler l’a­na­lyse pire-cas avec un modèle dyna­mique. On obtient ain­si des courbes décri­vant dans le temps les valeurs mini­males et maxi­males que peuvent prendre les indi­ca­teurs de per­for­mance de l’in­ves­tis­se­ment : volume, cash-flow, retour sur capi­tal employé…

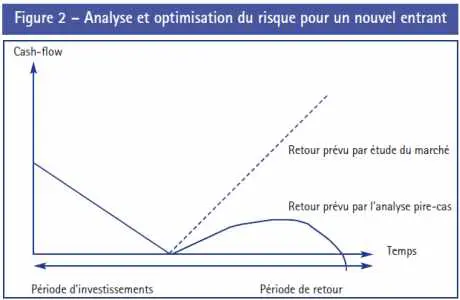
Pour illus­trer le type de résul­tats atten­dus de cette approche, consi­dé­rons par exemple le pro­blème d’un nou­vel entrant sur un mar­ché. Après une période ini­tiale d’in­ves­tis­se­ments, le déci­deur pré­voit un retour sur inves­tis­se­ment de 20 % (voir figure 2).

À par­tir d’in­ter­valles larges sur les para­mètres cri­tiques : taux de change, cours de matières pre­mières, entrée d’un concur­rent… l’a­na­lyse pire-cas cou­plée au modèle dyna­mique per­met de quan­ti­fier rapi­de­ment l’im­pact maxi­mum sur la ren­ta­bi­li­té et de garan­tir un retour mini­mum aux investisseurs.

Conclusion et perspectives

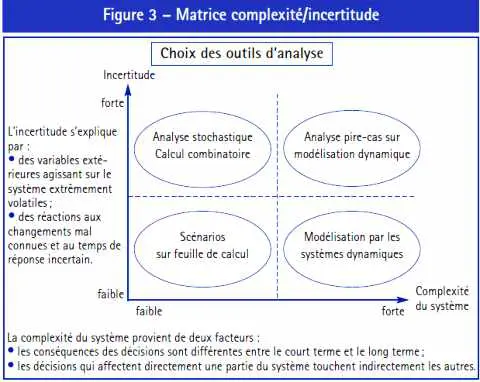
L’ap­proche pire-cas offre de nom­breuses pers­pec­tives inté­res­santes pour l’aide à la déci­sion stra­té­gique en envi­ron­ne­ment incer­tain en don­nant une garan­tie sur le cas le plus défa­vo­rable. Elle s’a­vère par­ti­cu­liè­re­ment utile pour les déci­sions stra­té­giques lourdes de l’en­tre­prise, où il n’y a pas de pos­si­bi­li­té de retour en arrière ni de sor­tie pen­dant une période rela­ti­ve­ment longue. Fina­le­ment, comme le montre la matrice complexité/incertitude (figure 3), l’ap­proche pire-cas s’ins­crit dans une pro­blé­ma­tique d’incertitude/complexité forte où elle est en mesure, plus que les autres ins­tru­ments d’a­na­lyse, d’ap­por­ter une aide à la déci­sion stratégique.

_______________________________
1. Ain­si, le logi­ciel KMV, sou­vent uti­li­sé en ana­lyse de risque de cré­dit, s’appuie sur cette méthode.

---

Articles similaires :

Com­merce élec­tro­nique. Mirage ou miracle économique ? Hen­ri Poin­ca­ré et la relativité Le géné­ral et les pierres précieuses L’EUROPE ET L’EMPLOI APRÈS AMSTERDAM (pre­mière partie) Dix ans d’aide aux PME