Isaac Newton, fondateur de la science occidentale
Conférence prononcée le 30 mars 1998 à l’amphithéâtre Henri Poincaré du ministère de l’Enseignement et de la Recherche, sous l’égide de la SEE et du CNISF.
La vie d’Isaac Newton
La chronologie, présentée sous forme d’encadré en fin d’article, rassemble les principaux événements de la vie de Newton, privée et publique. Je ne reprends ci-dessous que ceux qui sont susceptibles d’éclairer son œuvre.
Le siècle de Newton est aussi celui de Louis XIV. Le contraste est saisissant entre la stabilité politique de la France et l’instabilité de l’Angleterre. Newton a connu cinq monarques et deux révolutions. La situation s’inversera au cours des siècles suivants.
Newton est né en 1642, le jour de Noël, à Woolsthorpe, dans le Lincolnshire. Chétif, il vivra quatre-vingt-cinq ans. Son père meurt avant sa naissance. Sa mère, aisée, se remarie en 1645 avec un pasteur bien peu chrétien, qui laisse pendant huit ans l’enfant à la charge de sa grand-mère maternelle. De caractère renfermé, celui-ci a des relations difficiles avec les garçons de son âge. Il fabrique des meubles de poupées pour les filles. Il copie des dessins trouvés dans des livres et fabrique les objets correspondants, tels qu’une clepsydre qui fonctionne parfaitement. Aujourd’hui, les jeux électroniques et les jouets préfabriqués détruisent le goût du bricolage chez les nombreux enfants qui les possèdent. Newton a toujours conservé le goût du travail manuel et de la précision du détail.
Rentré chez sa mère à 17 ans, après la mort de son beau-père, il est admis à Trinity College (Cambridge) en qualité de « sizar » : il payait moins cher en échange de quelques services. Trois ans plus tard, en 1664, il devient étudiant à part entière. Pendant la grande peste de 1665–1666, il revient chez sa mère, à Woolsthorpe. C’est pendant ces deux ans qu’il faut situer l’origine de ses idées sur la gravité, sur les fluxions (calcul différentiel) et sur la théorie des couleurs. Mais, à cette époque, ses idées avaient la forme d’intuitions dont il était convaincu sans pouvoir les démontrer. Ne publiant rien lui-même, il accusait de plagiat ceux qui publiaient quelque chose qu’il avait déjà trouvé ; ce fut l’origine de nombreux conflits, notamment avec Robert Hooke, avec Flamsteed, l’astronome royal, et avec Leibniz.
Le caractère de Newton ne contribuait pas à aplanir les conflits. Il est méfiant, vindicatif, rancunier, inquiet, susceptible, irritable et ne supporte pas la critique. Solitaire et secret, ombrageux et taciturne, il a une crainte anormale de la controverse, mais, lorsqu’elle surgit, il s’y investit avec passion. Pendant son conflit avec Leibniz à propos du calcul différentiel, il rédige lui-même des libelles qu’il fait signer et distribuer par ses amis ! Il faut dire que Leibniz ne l’a pas cité, bien qu’ils aient correspondu sur le sujet. Taciturne et bûcheur, c’est un travailleur acharné, obsessionnel ; il lit beaucoup et systématiquement. Misanthrope, imbu de sa personne, sûr de lui, il n’éprouve pas le besoin de publier. Il ne s’intéresse pas aux femmes. Il a peu d’amis, mais des amis fidèles qui lui vouent un véritable culte. Le plus célèbre est Edmund Halley, qui écrit dans sa présentation des Principia : « Aucun mortel ne peut approcher plus près des dieux. »
Colérique et injuste lorsqu’il est contrarié, Newton sait se montrer généreux, notamment avec les jeunes étudiants. Il est parfois modeste, par exemple le jour où il déclare que, s’il voit loin, c’est qu’il est juché sur les épaules de géants. Ces géants sont Galilée, Copernic, Tycho Brahé et Kepler, dont il eut la patience de dénicher les trois lois dans des écrits confus (voir encadré).
LOIS DE KEPLER
|
La psychologie de Newton est sans conteste d’une grande complexité. Célébré comme un rationaliste par les Français des Lumières, il fut aussi vilipendé pour son arianisme et son penchant pour l’ésotérisme. Seule sa prudence lui permit de conserver sa chaire de Cambridge. Dans le langage d’aujourd’hui, on peut dire qu’il souffrait d’une forme de névrose teintée de paranoïa !
En 1680 sont observées deux comètes se déplaçant en sens inverse. Flamsteed, l’astronome royal, écrit à Newton, professeur de mathématiques à Cambridge depuis 1669, pour lui dire qu’il s’agit d’une seule et même comète qui a tourné devant le Soleil.
Newton répond qu’une comète unique serait tombée sur le Soleil, mais il se trompe dans ses calculs. Flamsteed le lui montre. Newton, vexé, ne le citera plus, bien qu’il ait besoin de lui pour obtenir certaines données sur la Lune. Il finit par admettre qu’il n’y avait bien qu’une comète, mais qu’elle était passée derrière le Soleil. Halley reprit plus tard le calcul de la trajectoire de la comète et prédit qu’elle devait revenir à la fin de 1758 ou au début de 1759. Clairaut, après un long calcul, affina la date à la mi-avril 1759, à un mois près. La comète passa à son périhélie le 14 mars : ce fut le premier triomphe de la mécanique céleste newtonienne.
Après la publication des Principia en 1687, Newton s’intéresse à la vie publique. Il défend l’Université contre Jacques II et, après la fuite de ce dernier, se fait élire membre du Parlement pour Cambridge. En 1696, il s’installe à Londres avec sa nièce, Catherine Barton, maîtresse de Charles Montague, Earl of Halifax et chancelier de l’Échiquier. Il participe à la vie mondaine, mais parle peu. En 1699, il présente à la Cour son nouveau sextant, dont Hooke revendique la paternité : nouvelle querelle ! Newton cherche un poste administratif et, en 1699, grâce à l’appui de Charles Montague, devient Warden of the Mint, puis Master, c’est-à-dire directeur de la Monnaie royale. Il remplit sa fonction avec sérieux et compétence ; il traque efficacement la fausse monnaie.
En même temps, de 1703 à 1727, il préside la Royal Society et règne en maître absolu sur la science anglaise. En 1705, il est fait chevalier par la Reine Anne pour ses travaux scientifiques ; c’est une première dans le monde des chevaliers.
Après la mort de Newton le 23 mars 1727, ses grandioses funérailles et son enterrement à Westminster, les savants anglais se gardent de marcher sur ses plates-bandes. Ainsi, Halley se livre à des travaux de thermodynamique et de météorologie. Ce sont les Français qui poursuivent les travaux de Newton. Voltaire s’en fait le propagandiste et Madame du Châtelet le traduit : Sir Isaac devient un héros des Lumières ! Pendant la Révolution et l’Empire, la France fut le phare de la science jusqu’à la défaite et la réaction romantique. Newton était le feu qui illuminait ce phare.
Il est temps maintenant de nous pencher sur les travaux scientifiques et ésotériques d’Isaac Newton.
La mécanique et les Principia
Comme toujours, l’élaboration laborieuse des idées de Newton en mécanique contraste avec la présentation rationnelle qu’il en donne dans les Principia (Principes mathématiques de philosophie naturelle). Newton commence par s’appuyer sur la 3e loi de Kepler (voir encadré) pour établir que la force centrifuge subie par une planète est proportionnelle à l’inverse du carré de sa distance au Soleil et qu’elle doit être équilibrée par une force d’attraction égale.
Ce n’est pas la bonne interprétation pour établir la forme de la trajectoire. Il semble que ce soit Robert Hooke qui lui ait suggéré, vers 1680, qu’il fallait imiter Galilée, qui avait décomposé le mouvement d’un projectile en un mouvement inertiel horizontal et un mouvement de chute vertical.
De même, pour interpréter par exemple le mouvement de la Lune, il faut le décomposer en un mouvement inertiel tangentiel et un mouvement de chute radial. Mais Hooke n’avait pas la patience de développer les calculs auxquels se livra Newton avec l’aide du calcul des fluxions. Newton aurait gagné beaucoup de temps s’il avait mieux lu Galilée.
Si ce qui précède est exact, l’anecdote de la pomme, qui aurait eu lieu à Woolsthorpe pendant la grande peste, serait une invention que Newton aurait peut-être contribué à répandre lui-même. Ce n’est que plus tard qu’il comprit que la Lune » tombait » sur la Terre comme la pomme, de même que les planètes « tombent » sur le Soleil. En exploitant cette idée, Newton a mis sur le même pied les pommes, les boulets de canon, la Lune et les planètes. La séparation scolastique du monde céleste et du monde sublunaire a vécu : le système solaire est gouverné par une même loi de « gravitation universelle ».
|
Figure 1 Démonstration par Newton de la loi des aires de Kepler pour une force centripète : le mouvement BC du satellite est la résultante du mouvement inertiel Bc et du mouvement de chute BV. |
Il semble bien que Hooke ait découvert par lui-même la loi du carré inverse de la distance, sans parvenir à en faire la démonstration. L’idée était dans l’air. Hooke en avait discuté avec Christopher Wren, l’architecte de Saint-Paul, et avec Edmund Halley, grand ami de Newton. Halley vient consulter Newton qui, en 1675, n’a encore rien publié dans le domaine de la mécanique. Newton envoie à Halley deux preuves différentes. Aiguillonné par la priorité que semble revendiquer Hooke, Newton commence à rédiger les Principia, dont Halley prend sur lui d’assurer la publication.
En fait, Hooke n’était pas, comme Newton, d’un caractère ombrageux et se serait contenté d’une mention dans la préface des Principia. Mais notre héros ne l’entendait pas de cette oreille : il ne cite Hooke ni dans sa préface ni dans aucune de ses publications ultérieures !
Rédigés en dix-huit mois, de 1684 à 1686, les Principia sont publiés en 1687. C’est une œuvre magistrale, d’une lecture difficile, construite en trois livres. Le premier livre traite des lois du mouvement et rend hommage, sans le citer, aux travaux de Galilée. L’auteur résout le problème de la composition des forces, tout en refusant de spéculer sur leur origine ; elles ne sont observables que par les accélérations qu’elles produisent. Il établit la conservation de la quantité de mouvement et de l’énergie dans le choc élastique de deux billes ou de deux pendules. Il déduit les trois lois de Kepler de la loi du carré inverse de la distance. Il s’appuie sur l’égalité de l’action et de la réaction pour démontrer que la masse d’une sphère homogène peut être concentrée en son centre.
La démarche de Newton se décompose en cinq étapes :
a) il énonce la loi d’inertie (voir encadré ),
b) il établit la relation entre l’accélération prise par une masse et la force qui lui est appliquée,>
c) il démontre la loi des aires de Kepler dans le cas d’une force centrale,
d) il déduit de la 3e loi de Kepler la loi du carré inverse de la distance,
e) il en déduit que la trajectoire d’une planète autour du Soleil est une ellipse dont le Soleil occupe l’un des foyers.
Le raisonnement de Newton pour démontrer la loi des aires se lit sur la figure 1, reproduite des Principia. Supposons que, pendant l’intervalle D t, la planète ait décrit le segment AB. Si elle n’était soumise à aucune force extérieure, le principe d’inertie nous dit que, pendant l’intervalle D t suivant, elle décrirait le segment Bc. En fait, en B, elle subit une force qui la fait « tomber » de B en V. Elle décrit donc en réalité le segment BC, diagonale du parallélogramme BVCc. On note d’abord que les triangles SAB et SBc ont même aire : ils ont même hauteur issue de S et deux bases égales AB et Bc. Ensuite, les triangles SBc et SBC ont même aire : le côté SB est commun et les hauteurs issues de c et de C sont égales, puisque Cc est parallèle à SB. Donc les triangles SAB et SBc ont même aire, C.Q.F.D.
On note que la loi des aires est vérifiée quelle que soit la forme de la force centripète, pourvu qu’elle soit centrale. Ce n’est que plus tard qu’intervient la loi du carré inverse de la distance, pour établir que la trajectoire est une ellipse. Le raisonnement de Newton est assez obscur et s’appuie sur des propriétés peu connues des ellipses. Richard Feyman a reconstitué un raisonnement plausible s’appuyant sur la décomposition de l’hodographe circulaire (diagramme des vitesses) en arcs égaux.
Le premier livre des Principia peut être considéré comme le premier manuel de mécanique théorique
Le second livre est consacré au mouvement des fluides. Newton postule que la résistance opposée par un fluide est proportionnelle au carré de sa vitesse. Il calcule la forme du solide de révolution de moindre résistance, jetant les bases du calcul des variations, qu’il utilise aussi pour résoudre le problème des brachistochrones (lignes de plus grande pente).
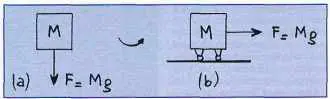 Figure 2 Masse pesante et masse inerte : dans les deux cas, la masse M prend l’accélération g sous l’effet de la force F. |
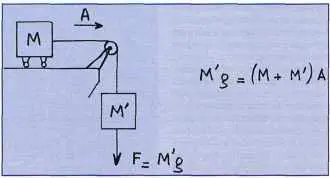 Figure 3 Masse pesante et masse inerte : M’ est une masse pesante à gauche et une masse inerte à droite. |
Il faisait preuve d’une grande maîtrise en mathématiques. Ayant reçu ce problème de Bernouilli un après-midi de 1696, il le résout avant d’aller se coucher ! Il aborde le traitement mathématique des vagues et calcule leur diffraction à travers un orifice. Il est surprenant qu’il n’ait pas fait à cette occasion un rapprochement avec la diffraction de la lumière, dont il avait fait une étude expérimentale très précise. Ce second livre, agrémenté de la description de nombreuses expériences, est le premier manuel d’hydrodynamique.
Le troisième livre porte sur les mouvements des satellites par rapport aux planètes et de celles-ci par rapport au Soleil. Newton y développe les bases du calcul différentiel, sous la forme du calcul des fluxions.
Sa notation x” de la dérivée par rapport au temps est encore utilisée aujourd’hui et est souvent plus commode que la notation dx/dt de Leibniz. Newton détermine la masse des planètes par rapport à la Terre. Il situe la densité de cette dernière entre 5 et 6, à comparer avec la valeur 5,5 admise aujourd’hui. Il en déduit la masse du Soleil et des planètes possédant des satellites. Il évalue l’aplatissement de la Terre à 1⁄230, contre 1⁄297 aujourd’hui. La vérification en fut faite après sa mort par les expéditions françaises en Laponie et au Pérou.
Newton calcule la précession des équinoxes et les variations de l’accélération de la pesanteur. Il évalue les irrégularités du mouvement de la Lune dues au Soleil, fondant ainsi la méthode des perturbations, sans parvenir à réduire l’écart entre calcul et observation à moins de 1⁄6 de degré. Laplace lui-même ne réussit pas à descendre au-dessous de 1⁄120 de degré. Il fallut attendre Henri Poincaré pour montrer que le comportement à long terme du système solaire était chaotique et était donc très sensible aux conditions initiales. Newton explique les marées océaniques (voir plus loin) et calcule l’orbite des comètes en procédant comme pour les planètes. Il démontre que la trajectoire peut être une conique quelconque. Ce troisième livre est le premier manuel de mécanique céleste.
Les Principia sont à l’origine de tous les développements ultérieurs de la mécanique et de la physique, y compris la physique quantique. Les d’Alembert, Lagrange, Laplace, Bernouilli, Poincaré, pour ne citer que les plus grands, ont perfectionné les mathématiques des Principia, sans sortir du cadre newtonien.
Aujourd’hui, les propriétés mécaniques des nanotubes de carbone sont déterminées par la méthode de la dynamique moléculaire, qui consiste à déduire les forces d’interaction moléculaires de la physique quantique, puis à les insérer dans un modèle newtonien pour étudier le comportement de la structure globale. La mécanique de l’ingénieur a conservé la forme la plus simple de la mécanique newtonienne, ce qui lui permet de traiter sans difficulté les systèmes dissipatifs, dont il est fait grand cas aujourd’hui en prétendant qu’ils nécessitent une « nouvelle alliance ».
Cependant, la mécanique des systèmes conservatifs a pris une forme particulièrement élégante sous la forme de la mécanique hamiltonienne. L’équation de Hamilton-Jacobi définit une famille de surfaces d’onde normales aux trajectoires des particules. Pour établir sa célèbre équation, Schrödinger a fait vibrer l’onde de Hamilton-Jacobi tout comme Fresnel a fait vibrer l’onde de Huygens pour fonder l’optique ondulatoire. La physique quantique découle de la mécanique hamiltonienne, donc de la mécanique newtonienne, comme l’optique ondulatoire découle de la théorie des ondes de Huygens. Le tableau serait parfait si Newton avait poursuivi jusqu’à leur terme ses idées sur l’optique des interférences. Mais il était trop attaché à son idée que sa dynamique devait pouvoir expliquer les phénomènes lumineux pour adopter un point de vue purement ondulatoire (voir plus loin l’Optique).
La masse
Dès ses premières réflexions, Newton se persuada qu’il était inutile de distinguer la masse inerte de la masse pesante et que ces deux masses étaient, non seulement équivalentes, mais identiques ; toutes les masses sont en fait des masses inertes, quelles que soient les circonstances.
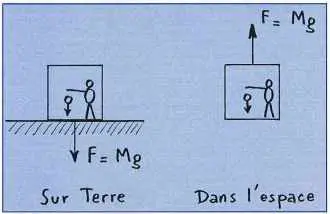 Figure 4 Première forme du principe d’équivalence : l’homme ne peut savoir s’il est dans une cabine reposant sur le sol ou dans une cabine accélérée vers le haut. |
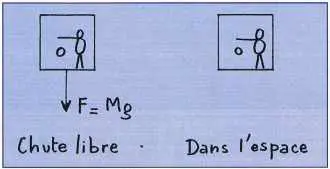 Figure 5 Seconde forme du principe d’équivalence : l’homme ne peut savoir s’il est dans une cabine en chute libre ou dans une cabine abandonnée dans l’espace. |
Cependant, avec son souci de la précision, il tint à le vérifier expérimentalement. Pour cela, il construisit neuf pendules constitués par des sphères creuses en bois, de même diamètre, qu’il remplit de diverses matières plus ou moins lourdes. Toutes ces sphères, également affectées par la résistance de l’air, avaient même période d’oscillation, ce qui établissait l’identité de la masse inerte et de la masse pesante et justifiait les dires de Galilée, pour qui, déjà, tous les corps tombaient dans le vide avec la même accélération. Newton décrit ces expériences dans le livre III des Principia.
Je crois que Newton aurait approuvé les conclusions que l’on peut tirer des figures 2 (a) et (b). Sur la figure 2 (a), une masse M tombe avec l’accélération g. Elle est donc soumise à une force F = Mg que l’on appelle son poids. Sur la figure 2 (b), un chariot de masse M roulant sans frottement sur des rails horizontaux est soumis à la force F : il prend une accélération g telle que F = Mg. Peu importe la méthode de mesure de M et de F ; on peut imaginer une balance et un peson. Le point important est que les figures 2 (a) et (b) se déduisent l’une de l’autre par une rotation de 90°. C’est la même masse sur les deux figures : c’est une masse inerte.
Considérons maintenant la figure 3, sur laquelle le chariot de masse M est accéléré par le poids d’une masse M”. Si A est l’accélération prise par le chariot, on a : M’g = (M + M”)A. Comment M” pourrait-elle ne pas être la même dans les deux membres ? Selon la terminologie habituelle, à gauche, c’est une masse pesante, à droite, une masse inerte. Newton avait raison de considérer ces deux masses comme identiques. Cette conclusion est justifiée a posteriori par la cohérence de toute la mécanique newtonienne, notamment de la mécanique céleste. La Lune et la pomme tombent toutes deux sur la Terre avec la même accélération.
Newton n’aurait pas été surpris par les deux formes du principe d’équivalence énoncé par Einstein dans les années 1910. Un homme isolé dans une cabine n’a aucun moyen de savoir si la cabine repose sur le sol terrestre ou si elle se trouve dans l’espace, loin de toute masse, accélérée par une force F = Mg perpendiculaire au plancher de la cabine (figure 4). Dans les deux cas, s’il lâche une pomme, elle tombe avec l’accélération g. De même, dans le cas de la figure 5, l’homme n’a aucun moyen de savoir si la cabine est en chute libre ou si elle flotte dans l’espace, loin de toute masse. Dans les deux cas, il ne sent pas son poids : lui-même et les objets qui l’accompagnent flottent librement à l’intérieur de la cabine. Bien qu’il parlât de « principe d’équivalence », Einstein était, comme Newton, intimement convaincu que masse inerte et masse pesante étaient identiques.
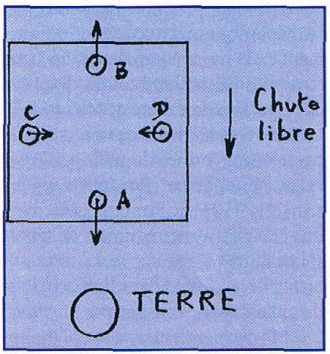 Figure 6 Forces de marées exercées par la Terre sur quatre billes contenues dans une cabine en chute libre. |
Cependant, si l’on regarde de plus près la situation de la cabine en chute libre de la figure 5, tous ses points ne subissent pas exactement la même accélération, car le champ de pesanteur n’est pas uniforme à l’intérieur de la cabine. Une bille A située près du plancher est plus fortement accélérée qu’une bille B près du plafond ; ces deux billes tendent donc à s’écarter (figure 6). Deux billes C et D situées près des parois tendent à se rapprocher, car elles sont accélérées vers le centre de la Terre. Si la section de la cabine est un carré de 5 m de côté et si elle est lâchée d’une hauteur de 250 m, le temps de chute est de 7 s, les billes A et B s’éloignent de 0,4 mm et les billes C et D se rapprochent de 0,2 mm. Dans le référentiel de la cabine, les billes subissent des forces appelées forces de marées.
Les marées océaniques s’expliquent de cette façon (figure 7). La Terre est dans le champ de gravité de la Lune. Les particules d’eau situées dans la direction de la Lune tendent à s’écarter comme les billes A et B ; celles qui sont sur les côtés tendant à se rapprocher comme les billes C et D. On comprend ainsi qu’il y ait deux marées hautes et deux marées basses par jour, par suite de la rotation de la Terre sur elle-même. Il est remarquable que Newton ait compris ce phénomène, qui n’a rien d’évident. Si vous posez la question aux personnes, même cultivées, qui vous entourent, bien peu seront capables de vous fournir une explication satisfaisante.
En fait, le comportement des marées est plus compliqué, d’une part en raison de la forme des côtes, d’autre part par suite de la combinaison des effets de la Lune et du Soleil. Deux fois par mois lunaire, aux moments de la pleine Lune et de la nouvelle Lune, l’effet du Soleil vient renforcer celui de la Lune et les marées sont plus fortes. Ce renforcement dépend de l’inclinaison de l’orbite lunaire sur l’orbite terrestre : il est minimal aux moments des solstices et maximal aux moments des équinoxes.
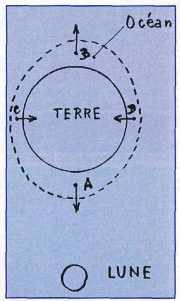 Figure 7 Forces de marées exercées par la Lune sur quatre particules océaniques. |
Soit maintenant une cabine spatiale (figure 8), d’abord en mouvement rectiligne, uniforme, que l’on force à un certain moment, par exemple au moyen d’une petite fusée, à adopter une trajectoire à courbure constante. La cabine contient une bille contrainte par deux ressorts jouant le rôle d’accéléromètre.
Dans le référentiel de la cabine, la bille subit la force centrifuge et s’écarte de sa position d’équilibre dès que la trajectoire s’incurve. Le principe d’inertie n’est plus vérifié. On peut refaire de la cabine un référentiel d’inertie en remplaçant l’accélération de la fusée par celle d’un champ de gravité. La cabine et la bille subiront alors la même accélération de gravité et la bille reprendra sa position d’équilibre. Elles tombent ensemble dans le champ de gravitation comme la Lune dans celui de la Terre.
Dans le langage de la théorie quantique des champs, un tel champ compensateur, qui rétablit la symétrie brisée par la courbure, est appelé champ d’invariance de jauge, le mot « jauge » étant pris dans le sens de référence. Le champ de pesanteur est un champ d’invariance de jauge. Si la courbure varie, ce champ doit lui aussi être variable : l’invariance de jauge, qui était globale, devient locale. Ainsi, un champ de gravitation variable permet de rendre compte de tout mouvement de la cabine sous la forme d’un mouvement libre. Il est ainsi possible de donner au satellite un mouvement quelconque tout en conservant son caractère de référentiel d’inertie.
Nous pouvons maintenant donner une définition précise d’un référentiel d’inertie ou référentiel galiléen : un référentiel d’inertie est un référentiel en mouvement libre (en chute libre) dans un champ de gravité quelconque. Ainsi se trouve éliminé le côté vicieux de la définition antérieure, qui disait à peu près : le principe d’inertie est vérifié dans un référentiel d’inertie ; un référentiel d’inertie est un référentiel dans lequel est vérifié le principe d’inertie !
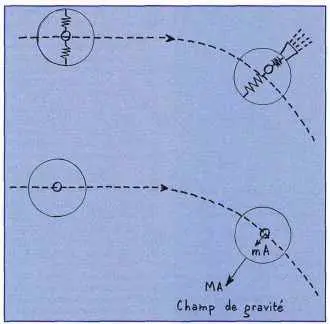 Figure 8 Si la trajectoire s’incurve sous l’effet d’une force extérieure, la bille contenue dans la cabine est soumise à la force centrifuge ; la cabine n’est plus un référentiel d’inertie. Elle le redevient si la courbure est due à l’action d’un champ de gravité, qui joue le rôle d’un champ d’invariance de jauge. |
Einstein a dû beaucoup penser à Newton pendant les années où il élaborait à grand-peine la relativité générale en s’initiant au calcul tensoriel sous la houlette de son ami Grossmann. Il fit sienne l’idée newtonienne de l’identité de la masse inerte et de la masse pesante ; les champs de gravité et d’accélération sont donc interchangeables.
Il comprit alors que la trajectoire d’un mobile en mouvement libre dans un champ de gravité variable pouvait être identifiée à une géodésique d’un espace-temps courbé par la matière source de la gravité ; de plus, cet espace-temps courbe doit être localement lorentzien, pour être en règle avec la relativité restreinte. Il est dommage que la beauté intrinsèque de cette théorie se traduise par des équations tensorielles insolubles, sauf dans le cas très particulier de la symétrie centrale, qui est heureusement celui des trous noirs.
Il est donc faux de prétendre que la mécanique einsteinienne est la négation de la mécanique newtonienne, comme le proclame imprudemment le livre La mort de Newton, imprudemment préfacé par Stephen Hawking, successeur de Newton à Cambridge.
La mécanique einsteinienne est le prolongement naturel de la mécanique newtonienne.
Einstein est le fils spirituel de Newton, dont il a poussé les idées à leur terme et qu’il a libéré du dilemme que constituait pour lui la transmission instantanée d’une force à distance, en remplaçant la dynamique par la géométrie de l’espace-temps, dont les déformations se propagent à la vitesse de la lumière. Newton n’a donc plus besoin de dire : « Tout se passe comme si… » J’ai repris la formule en biologie, qui attend toujours son Einstein, sous la forme de ce que j’appelle la « finalité objective ».
LOIS DE NEWTON
|
L’optique
Newton commence à enseigner l’optique après avoir pris la chaire de mathématiques de Barrow en l669. Il dépose à l’Université un texte intitulé Lectiones Opticae, qui ne sera publié qu’après sa mort, en 1729. En 1668, après avoir essayé de fabriquer des lentilles asphériques, il se rend compte que les aberrations sphérique et chromatique empêchent de fabriquer un télescope réfringent de bonne qualité. Il fabrique alors un télescope à réflexion grossissant 40 fois ; il élabore son propre alliage, coule et polit lui-même son miroir. En 1671, il présente son appareil à la Royal Society. À 29 ans, il est inconnu et n’a encore rien publié. Il écrit une lettre trop humble à Oldenburg, secrétaire de la Royal Society, accompagnée d’une communication sur l’optique, dans laquelle il décrit ses expériences de décomposition et de recomposition de la lumière blanche au moyen de prismes.
Dans une expérience cruciale, Newton isole un rayon bleu et un rayon rouge. Un second prisme ne modifie pas leur couleur, mais le rayon bleu est plus dévié que le rouge. Il écrit : « La lumière se compose de rayons de diverses réfringences. » Cette expérience est à l’origine de la description de l’aberration chromatique qu’il donnera dans son Optique. De nombreuses critiques se font entendre, au sein même de l’Académie. Newton en est ulcéré : il écrit à Leibniz qu’il regrette d’avoir présenté sa communication ! Il est particulièrement touché par les critiques exprimées par Huygens et par Hooke. La querelle qui en résulte avec ce dernier est exacerbée par Oldenburg, qui n’aime pas Hooke ! Newton attendra la mort de Hooke, survenue en 1703, avant de publier son Optique en 1704.
Cette querelle ne l’empêche pas de soumettre à la Royal Society, en 1675, une deuxième communication sur la lumière. Pour lui, l’espace est rempli d’un éther subtil dans lequel se propagent des grains de lumière de masses différentes, selon leur couleur ; les grains rouges sont plus lourds que les violets. Selon Newton, la vitesse de la lumière dans un milieu est proportionnelle à sa réfringence (indice de réfraction), elle-même proportionnelle à sa densité. En appliquant sa dynamique aux grains de lumière, il retrouve les lois de la réfraction et de la réflexion. C’est dommage, car ce succès trompeur et partiel le conforte dans son erreur et l’empêchera de découvrir l’optique ondulatoire.
Dans cette même communication, Newton présente un grand nombre d’expériences très soignées, effectuées en lumière blanche et monochromatique sur les bulles de savon, les couches minces et les lames minces créées entre une lentille convexe et un plan. Il établit que les anneaux observés dépendent de l’épaisseur traversée et de celle de la lame et qu’en lumière blanche on obtient les mêmes teintes quand les épaisseurs sont multiples les unes des autres. Les anneaux se resserrent quand l’épaisseur augmente et on en observe un plus grand nombre en lumière monochromatique. Par transmission, on obtient les couleurs complémentaires de celles qu’on observe par réflexion.
Pour rendre compte de ces phénomènes, Newton élabore sa theory of fits, appelée en français « théorie des accès », le mot « accès » étant pris dans le même sens que dans l’expression « accès de fièvre ». Il fait l’hypothèse que, quand un corpuscule frappe le front séparant deux milieux, il fait vibrer l’éther, qui est plus dense par exemple dans le verre que dans l’air. La vibration se propage plus vite que le grain de lumière et, quand elle atteint une deuxième surface de séparation, elle met, selon sa phase, le milieu dans un état transitoire – un accès – qui favorise la réflexion ou la réfraction
Il n’est pas exagéré de dire que Newton était à deux doigts de la théorie ondulatoire de Fresnel. Hooke avait déjà observé les anneaux de Newton et les couleurs des bulles de savon. Mais il était trop dilettante pour faire les efforts nécessaires pour leur trouver une explication physique. Celle de Newton était très près de la vérité. Mais il tenait trop à sa théorie mécaniste de la lumière pour l’abandonner. Ses expériences très fines sur la diffraction, à la suite de Grimaldi, seront suivies d’explications invraisemblables.
En tout cas, il est profondément injuste d’opposer, comme on le fait trop souvent, la théorie corpusculaire de Newton et la théorie ondulatoire de Huygens. L’onde de Huygens n’explique ni les interférences ni la diffraction. L’optique ondulatoire a été créée par Fresnel, qui eut l’idée de faire vibrer l’onde de Huygens. Quant à la théorie de Newton, elle est à la fois corpusculaire et ondulatoire : elle préfigure la dualité ondes-corpuscules. Michelson a écrit : « Newton a mesuré la grandeur que nous appelons aujourd’hui longueur d’onde et a montré que chaque couleur du spectre était caractérisée par une longueur d’onde déterminée. »
Newton développe ses idées dans son Optique publiée en 1704. Il explique la synthèse additive et soustractive des couleurs, ainsi que les couleurs de l’arc-en-ciel. Dans la seconde édition de 1717 figurent des « Questions » (Queries). L’une d’elles concerne la double réfraction du spath d’Islande. Newton avance l’idée que les grains de lumière ont des côtés, c’est-à-dire des propriétés transversales, idée dont ses successeurs se souviendront. Il montre que l’erreur d’aberration sphérique est proportionnelle au cube de l’ouverture et que l’erreur d’aberration chromatique lui est proportionnelle. Il décrit en détail la fabrication des miroirs métalliques et l’usage de la poix pour leur polissage. Il montre comment un prisme à angle droit peut être utilisé comme réflecteur. Il indique que l’agitation de l’air impose des limites aux performances que l’on peut attendre d’un télescope.
Bref, l’Optique de Newton est le premier manuel d’optique théorique et expérimentale.
L’alchimie et l’hermétisme
On évalue à une dizaine d’années le temps passé par Newton aux travaux rationnels qui ont fait sa gloire. Le reste du temps, il a accumulé deux millions de mots dans les domaines de la théologie, de l’alchimie et de l’hermétisme, qui le passionnaient. Beaucoup de ces textes sont des copies de manuscrits anciens. Connus sous le nom de Plymouth papers, on les a trouvés dans un coffre transporté de Cambridge à Londres quand Newton vint s’y installer en 1696. Considérés comme sulfureux, ils furent dispersés lors d’une vente en 1936, mais un peu plus de la moitié purent être rachetés par le célèbre économiste Lord John Maynard Keynes et légués à l’université de Cambridge.
Sur le plan religieux, Newton ne croyait pas à la Trinité, disant qu’elle résultait de la falsification des Écritures originales. Il était arianiste, proche du monothéisme judaïque de l’école de Maïmonide. C’est la raison pour laquelle il refusa les ordres et dut en être dispensé pour pouvoir enseigner. Il convertit à ses vues plusieurs de ses amis, dont Halley et son successeur à la chaire de mathématiques, Winston. Il se tint coi lorsque ce dernier fut chassé de l’Université pour arianisme, ce qui n’est certes pas à porter à son crédit.
Dans le domaine de l’alchimie, Newton se comporta, comme en mécanique et en optique, en expérimentateur scrupuleux, passant vingt-cinq ans dans son laboratoire et s’y livrant à des expériences interminables qui pouvaient durer toute la nuit. Au beau milieu de la rédaction des Principia, il y passe six semaines ! Ce n’est qu’à partir de 1690 que son intérêt pour l’alchimie commence à décliner. Il a compris qu’il était parvenu à des connaissances d’un nouveau genre qui ne devaient rien à l’hermétisme dont il était jusque-là imprégné. Seules comptent les relations mathématiques, comme il l’explique dans le Scholium generale qui ouvre le livre III des Principia. C’est là qu’on peut lire la fameuse phrase : Hypothesis non fingo.
On a beaucoup épilogué sur les tendances de Newton à l’ésotérisme et à l’hermétisme. Dans son livre La revanche des sorcières, Pierre Thuillier note que cette tendance était dans l’air du temps et que la raison n’a pas soudainement éliminé la magie. Le Siècle des lumières est le XVIIIe et non le XVIIe. Si Descartes revendiquait l’indépendance de la pensée, tout en conservant une conception dualiste de l’homme, il éprouva le besoin de s’exiler pour sa sécurité. Il y aurait eu des messes noires à Versailles. De toute façon, la magie n’a pas disparu du tout : elle progresse à grands pas et les idées de Newton auraient de nos jours le plus grand succès. Le New Age lui doit beaucoup ! Il n’est pas plus scandaleux de voir Newton s’intéresser de près à l’hermétisme que de voir des physiciens renommés s’appuyer sur la science pour démontrer la réalité des pseudophénomènes paranormaux. Si Newton était bien le premier des physiciens, il n’était pas le dernier des magiciens !
Chez Newton, l’ancien et le nouveau se mêlent de façon inextricable. Il croit que la Nature est une énigme dont les clés mystiques étaient connues des anciens philosophes, dont les écrits hermétiques auraient contenu de profondes vérités philosophiques et spirituelles. « Il regardait l’Univers comme un cryptogramme composé par le Tout-Puissant. » (Lord Keynes). Il avait le culte de la sagesse antique : les Anciens avaient des secrets cachés dans des symboles et dans un langage mystique. Pythagore connaissait la gravitation universelle.
C’est pourquoi il se livre pendant vingt-cinq ans à une étude méthodique des textes anciens, à la recherche de ces secrets perdus. Il a cherché le rationnel dans l’hermétisme et ne l’y a pas trouvé. Il n’était ni le premier ni le dernier. Il est remarquable que cet état d’esprit obscurantiste ne l’ait pas empêché de faire les grandes découvertes qui l’ont rendu célèbre.
La conception du monde de Newton est à la fois déiste et animiste. « Il existe un Esprit infini et omniprésent dans lequel la matière se meut selon des lois mathématiques. » Cette conception l’aide à admettre l’action instantanée à distance des corps les uns sur les autres, grâce aux « principes actifs » des alchimistes. En d’autres termes, la matière est animée ; il y a des interactions entre matière et Esprit. Bien entendu, j’écris « Esprit » avec une majuscule, afin de le distinguer de l’esprit ordinaire de la pensée. Mon scepticisme m’empêche de me rallier à cette analyse, mais c’est ainsi que fonctionnait le cerveau de Newton.
Conclusion
Isaac Newton a vraiment été le premier des physiciens. Par son exemple et par ses textes publiés, il a introduit la nécessité de la rigueur, de la cohérence et de la précision, de la vérification expérimentale et quantitative. Par son « Tout se passe comme si… », il reconnaît par avance la distinction qu’il convient d’établir entre la réalité objective et les modèles scientifiques. Mais c’est sans doute là une forme de falsification rétrospective. En effet, Newton a une vision unitaire du savoir. C’est un scientifique, mais aussi un théologien, qui conteste le mécanisme de Descartes, et un métaphysicien, qui fait siennes certaines thèses hermétistes. Connaissant aussi la Loi et l’Histoire, on peut dire de lui qu’il était l’un des derniers philosophes universels.
Lagrange et Laplace considéraient tous deux Newton comme le plus grand génie ayant jamais existé.
Boltzmann écrivait : « Les Principia sont le premier et le plus grand ouvrage de physique théorique. »
Et le grand Einstein : « Il combinait en une personne l’expérimentateur, le théoricien, le mécanicien et l’artiste dans l’expression. »
Mais c’est lui faire un mauvais compliment que de dire que « la Nature était pour lui un livre ouvert ». Il mit vingt ans à mettre en forme les idées qui lui étaient venues pendant la grande peste, quand il avait 23 ans. Newton était capable d’un effort mental plus soutenu que quiconque avant ou après lui. Quand on lui demandait comment il avait découvert la gravitation universelle, il répondait : « En y pensant toujours. »
On trouve dans ses écrits des idées prémonitoires qui n’acquerront un sens que beaucoup plus tard. Il pensait qu’il y avait dans la matière des forces attractives et répulsives qui devaient permettre de transmuter les corps les uns dans les autres. Parmi les Questions accompagnant la 2e édition de l’Optique, on trouve cette phrase étonnante :
« La transformation des corps en lumière et de la lumière en corps est très conforme au cours de la Nature, qui semble se complaire aux transmutations. »
Dans la Question suivante, qui est aussi la dernière, il évoque une théorie chimique fondée sur des forces électriques :
« Les attractions de la gravité, du magnétisme et de l’électricité atteignent des distances sensibles…, mais il peut y en avoir d’autres qui atteignent des distances si petites qu’elles échappent à l’observation et peut-être des attractions électriques atteignant des distances aussi petites, même sans être excitées par le frottement. »
Bien sûr, il serait stupide de prétendre que Newton a inventé l’effet photoélectrique et la théorie électromagnétique, mais ces citations montrent bien l’universalité de sa pensée et la portée de son imagination.
En tout cas, Newton avait pleinement conscience des difficultés de sa tâche, comme le montre le passage suivant, souvent cité :
“ Je ne sais pas ce que le monde pensera de moi. Pour ma part, j’ai l’impression de n’avoir été qu’un enfant qui joue sur la plage et se divertit en trouvant ça et là un coquillage plus joli qu’à l’ordinaire, alors que le grand océan de la Vérité reste inexploré devant moi. ”
Le caractère fuyant et fractal de l’horizon des connaissances ne lui avait pas échappé.
CHRONOLOGIE
|
BIBLIOGRAPHIE
|