La chimie quantique
Introduction
Introduction
La chimie étudie des molécules où les atomes sont connectés par des liaisons. Elle étudie aussi des réactions au cours desquelles certaines liaisons se forment et d’autres se rompent. Les liaisons étant faites d’électrons, les problèmes chimiques sont donc des problèmes d’arrangement d’électrons, régis par la mécanique quantique. En fait, certains concepts importants (valence, liaison covalente, aromaticité…) développés empiriquement au XIXe siècle n’ont reçu une interprétation – quantique – qu’au XXe siècle.
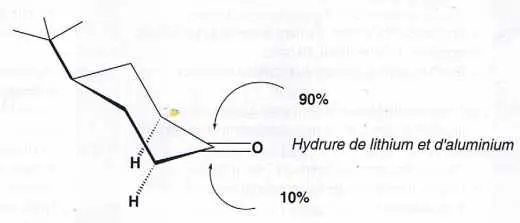
Depuis une cinquantaine d’années, les chimistes découvrent pour ainsi dire chaque jour des phénomènes inexplicables par la physique classique. Soit par exemple la 4‑terbutylcyclohexanone (figure 1). Le plan formé par le groupe carbonyle C = O et les deux carbones voisins définit deux demi-espaces. L’inférieur ne contient que deux atomes d’hydrogène. Tous les autres atomes de la molécule se trouvent soit dans le plan, soit dans l’autre demi-espace, donc davantage encombré. Cependant, quand on fait réagir cette molécule avec l’hydrure de lithium aluminium, à plus de 90 % le réactif attaque par la face supérieure, celle la plus encombrée.
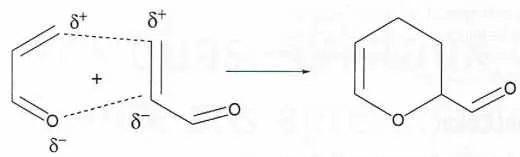
Quand on chauffe de l’acroléine, ce composé s’additionne à lui-même, et les atomes qui se lient portent des charges de même signe.
De tels résultats paradoxaux sont légion. Toute étude rationnelle de la chimie passe nécessairement par une théorie quantique. Malheureusement, une telle description est malaisée à mettre en œuvre. En effet, les problèmes chimiques sont des problèmes quantiques à N corps, avec N largement supérieur à 3 et on ne sait pas résoudre analytiquement les équations correspondantes. Deux familles de méthodes ont été développées.
Les méthodes numériques
Certains théoriciens, dont W. Kohn et J. A. Pople (colauréats du Nobel 2000), ont développé des méthodes numériques de résolution de l’équation de Schrödinger, donnant des résultats quantitatifs parfois d’une remarquable précision. Ces calculs sont traditionnellement – et un peu abusivement – qualifiés de calculs ab initio car, à l’exception de quelques approximations de base, toujours les mêmes (approximation de Born-Oppenheimer, approximation orbitalaire…), aucune autre hypothèse simplificatrice n’est utilisée lors de la résolution numérique des équations du problème.
Par ailleurs, des raffinements sont introduits pour corriger les erreurs dues aux approximations de base. Ainsi, l’approximation orbitalaire équivaut à traiter les électrons de manière indépendante. Les calculs dits d’interaction de configurations permettent de tenir compte de la répulsion mutuelle de ces électrons.
L’importance de ces travaux est indéniable. Le test ultime d’une théorie n’est-il pas, après tout, de prédire quantitativement les mesures expérimentales ? Ces calculs présentent de graves limitations cependant.
Un calcul numérique, contrairement à une solution analytique, n’offre qu’un résultat chiffré, pas une solution générale. Au lieu de fournir l’équation de la surface de potentiel E = f(qi) représentant l’énergie du système en fonction des coordonnées de ses atomes, le calcul ne donne qu’un point de cette surface. Le chemin réactionnel conduisant de la vallée des réactifs à celle des produits en passant par le col le plus bas (état de transition) doit être péniblement calculé point par point. Bref, les calculs ab initio, exigeant beaucoup de temps et d’effort, ne peuvent être un outil à tout faire, mais doivent plutôt servir à peaufiner un problème déjà dégrossi.
Contrairement à ce que l’expression ab initio donne à espérer, ces calculs ne peuvent être utilisés pour un traitement objectif du problème, évitant les idées préconçues de l’utilisateur. Certes aucune approximation arbitraire n’est introduite lors de la résolution des équations. Mais bien d’autres interviennent lors de la mise en équation du problème. En effet, on ne peut jamais calculer une réaction, mais seulement un modèle.
Au laboratoire, il n’est pas rare qu’un chimiste travaille avec une millimole de produit. Une millimole représente 6 1020 molécules. À titre de comparaison, l’âge de l’Univers (# 15 milliards d’années) correspond à 1017 secondes. La puissance des ordinateurs n’étant pas illimitée, plus les calculs sont raffinés, plus les modèles seront frustes. Et on arrive au résultat paradoxal suivant : l’outil étant très sûr, il ne pourra être mis dans toutes les mains ! Seuls les meilleurs chimistes sont capables d’inventer des modèles simples mais cependant significatifs.
Modéliser un système de 1020 molécules par trois ou quatre molécules est une gageure. Aussi, les calculs ab initio présentent peu d’intérêt pour l’enseignement du premier et second cycles, les étudiants ne connaissant encore pas assez de chimie pour les employer avec profit. Les exercices possibles sont peu nombreux, vu les temps d’ordinateur nécessaires à chaque problème. Enfin, personne n’étant capable de suivre l’évaluation de millions d’intégrales, le logiciel est employé plus ou moins comme une boîte noire, ce qui n’est guère formateur.
Par ailleurs l’étudiant, comme le chimiste professionnel, a rarement besoin d’un résultat numérique précis, mais plutôt de règles générales, d’idées directrices lui permettant de s’orienter dans le dédale des réactions chimiques. Les calculs numériques, résolvant les problèmes au coup par coup, ne peuvent fournir de telles règles. Et puis, ce n’est pas parce que l’ordinateur m’a donné un nombre, si précis soit-il, que je comprends le problème. En revanche, je peux prétendre le comprendre si je peux prédire l’ordre de grandeur du résultat et donner les raisons (basées sur quelques hypothèses fondamentales de la physique) pour lesquelles la machine doit nécessairement nous donner telle énergie, telle géométrie…
Il est clair que le chimiste doit pouvoir disposer d’une seconde famille d’outils, complémentaires des calculs numériques, et satisfaisant à ces critères. Actuellement, trois outils qualitatifs sont utilisés.
Les méthodes qualitatives
Les diagrammes de corrélation ont été appliqués à l’étude de réactions à partir de 1965 par H. C. Longuet-Higgins, L. J. Oosterhoff, et surtout par R. B. Woodward (prix Nobel 1965 pour ses synthèses totales) et R. Hoffmann (prix Nobel 1981, partagé avec K. Fukui). La méthode consiste à suivre par continuité la transformation du système de départ en produits d’arrivée. Si à un état fondamental correspond un autre état fondamental, la réaction requiert peu d’énergie et est dite » permise » par voie thermique. Si le diagramme fait correspondre un état excité à un état fondamental, l’énergie d’activation sera importante et la réaction » interdite « …
Si le système possède des éléments de symétrie se conservant au cours de la réaction, le tracé du diagramme exige seulement le calcul des systèmes de départ et d’arrivée. La méthode, très puissante, est cependant d’un maniement délicat, les systèmes réels étant rarement symétriques. Il faut donc les » symétriser » et parfois, mais c’est plus rare, réduire leur symétrie. Une modélisation maladroite conduit à des résultats aberrants.
Une seconde méthode, très simple, fut introduite par M. J. S. Dewar et H. E. Zimmerman dans les années 1970, mais ne s’applique qu’à des réactions dans lesquelles les atomes extrémités des liaisons créées ou rompues forment un cycle dans l’état de transition. Si ce cycle est » aromatique » (resp. » antiaromatique »), l’énergie d’activation est faible (resp. importante) et la réaction sera » permise » (resp. » interdite »).
L’approximation des orbitales frontières n’est pas soumise aux restrictions des méthodes précédentes.
Ces orbitales (la plus haute orbitale moléculaire occupée et la plus basse orbitale moléculaire vacante) équivalent pour les molécules aux orbites de valence pour les atomes. Quelle que soit la complexité du système, il suffira donc d’examiner deux orbitales par réactif. Le meilleur chemin réactionnel est alors celui optimisant les interactions des orbitales frontières. La méthode est donc très simple et très générale.
L’importance des orbitales frontières, suggérée dès 1952 par Fukui, n’a été acceptée qu’à partir de la fin des années 1970, grâce d’une part aux nombreux succès, d’autre part à une justification rigoureuse de l’approximation. Fukui a en effet montré que les orbitales frontières se détachent des autres orbitales moléculaires dans l’état de transition, ce qui explique leur rôle spécial. Ce travail explique aussi les quelques échecs de la méthode, appliquée à des modèles irréalistes de l’état de transition.
Conclusion
Il n’existe donc pas de méthode miracle pour appliquer la mécanique quantique à la chimie. La meilleure démarche semble être de dégrossir le problème par des méthodes qualitatives, d’affiner les résultats par des calculs ab initio et de vérifier expérimentalement les prédictions théoriques. À chaque instant, une bonne modélisation du problème, qui implique une connaissance assez approfondie de la chimie, est essentielle.
Pour un chimiste théoricien, de solides connaissances de mathématiques et de physique sont nécessaires, mais pas suffisantes. Laissons le mot de la fin à C. A. Coulson, qui fut titulaire de la chaire Rouse Ball de mathématiques à Oxford et l’un des meilleurs chimistes théoriciens du XXe siècle : » Contrary to what is sometimes supposed, a theoretical chemist is not a mathematician, thinking mathematically, but a chemist, thinking chemically. »