La loi des grands nombres en assurance : ni nécessaire ni suffisante
L’assureur vend des promesses, et fait appel pour cela à une multiplicité de techniques. Le chef d’entreprise (comme le contrôleur des assurances) doit donc comprendre à la fois :
- le 2 + 2 = » 4,00 » des comptables,
- le 2 + 2 = » combien voulez-vous que cela fasse » des actuaires,
- le 2 + 2 = » 3,999999999 » des informaticiens,
- et le II + II = IV des juristes.
Le résultat de l’assureur est aléatoire : il espère faire un bénéfice mais peut aussi faire une perte.
Pour éviter, à défaut d’une perte, du moins une perte qui le » ruine « , il se repose sur une loi de la statistique qui s’appelle la loi des grands nombres.
Les engagements réciproques de l’assuré et de l’assureur constituent le contrat d’assurance
Prenons trois exemples simples aussi variés que possible : A, agriculteur, court le risque de voir sa récolte détruite par la grêle ; C, chasseur, court le risque de blesser un promeneur ; D, père de famille, court le risque de décéder avant que ses enfants ne soient en âge de gagner leur vie.
En cas de réalisation du risque, A ne pourra pas assumer financièrement la perte d’une année de revenu, C le remboursement des frais de soins du promeneur et l’épouse de D la charge de plusieurs années d’éducation, d’alimentation, d’habillement, de ses enfants. Dans chacun de ces trois exemples, ces hommes sont confrontés à un risque et décident de s’assurer.
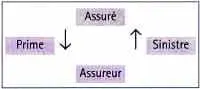Exposé à un risque,
- l’assuré paie à l’assureur une prime,
- l’assureur garantit que, si le risque se réalise, il paiera un sinistre.
Cet engagement réciproque (paiement de la prime convenue contre paiement, le cas échéant, de sinistres garantis) constitue le contrat d’assurance. Les deux parties au contrat ignorent donc si l’assureur aura un quelconque paiement à effectuer au profit de l’assuré. C’est en ce sens que le contrat d’assurance est un contrat aléatoire.
Le schéma précédent est-il vrai ? Oui, il est vrai, aussi vrai que la phrase » les oiseaux volent « , aussi vrai mais pas plus : tout le monde admet que la phrase » les oiseaux volent » est vraie, tout en sachant que l’autruche (qui est un oiseau) vole mal.
Le schéma général précédent appelle donc de nombreuses nuances et précautions de vocabulaire pour être juridiquement exact, il y a parfois lieu de distinguer, dans un contrat d’assurance, l’assuré qui court le risque, le souscripteur qui signe le contrat, le bénéficiaire qui perçoit, le cas échéant, la prestation de l’assureur : l’assurance de D peut avoir été souscrite par son employeur et comporter son conjoint comme bénéficiaire… Dans le même ordre d’idées, dans les assurances où l’événement qui déclenche la prestation est la survie de l’assuré ou la naissance d’un enfant, il ne serait pas très commercial de parler de sinistre…
Mais comme notre propos n’est pas de faire du droit ni du commerce, nous n’irons pas plus loin sur ce terrain.
Un risque mal diversifiable par les assureurs français : la tempête. © ALAIN TOSETTI
C’est la loi des grands nombres qui permet la compensation des risques
Réduite à un seul contrat avec un seul assuré, l’opération précédemment décrite serait un pari pour l’assureur. En effet, si le risque ne se réalise pas, l’assureur fait un petit bénéfice (la prime). Dans le cas contraire, si le risque s’est réalisé, il peut faire une perte importante. Il suffit de penser à l’assuré qui ayant calé à un passage à niveau avait fait dérailler un train, soit quelques millions de francs de dégâts à la charge de son assureur : pour pouvoir payer ces dégâts, ce dernier avait évidemment reçu les primes d’un grand nombre d’autres assurés !
Pour que chaque opération d’assurance ne soit pas un pari dont la perte entraîne sa faillite, l’assureur doit avoir réuni un grand nombre d’assurés : ex ante, l’assureur envisage de payer, avec les primes reçues de tous, les sinistres qui frapperont les malchanceux.
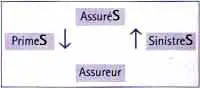La mutualisation des risques n’est possible que s’il n’y a pas un trop grand écart entre le nombre de malchanceux réels et ceux qu’il avait prévus. C’est la loi des grands nombres qui permet à l’assureur de s’engager à verser la somme aléatoire S des sinistres en ayant reçu la somme P (où P = n . π si chacun des n assurés paye la même prime π).
L’assureur ne s’engage pas seulement à payer les sinistres, mais aussi à les gérer : la prime payée par l’assuré comprend des chargements de gestion (et aussi des chargements de sécurité permettant à l’assureur d’espérer un bénéfice).
La loi des grands nombres dit en effet que, sous certaines conditions, le montant aléatoire S est » proche » du nombre certain P = n . π (si n est » assez » grand), et que ce montant peut être d’autant mieux prévu que le nombre d’assurés n est plus grand.
Prenons un exemple : un contrat d’assurance qui garantit le versement d’un capital de 100 000 F en cas de décès, souscrit par 10 000 assurés qui ont chacun une probabilité 1 % de décéder dans l’année.
Le calcul des probabilités nous dit que l’espérance mathématique du nombre aléatoire D de décès qui auront lieu dans l’année qui vient est de 1 %. 10 000 = 100, ce qui peut paraître évident. Il est évident aussi que le nombre de décès d qui aura réellement lieu ne sera pas égal à 100 sauf miracle : il y aura un écart entre d et D. L’écart » type » encore appelé déviation » standard » entre d et D est, nous dit la théorie, d’environ 10 (très exactement 9,95), et il y a une quasi-certitude (99,9 % de chances) que le nombre de décès réel sera égal à 100 à 3,3 écarts types près soit à 33 % près.
Si l’assureur a fait souscrire 1 000 000 d’assurés, les mêmes formules conduisent à dire qu’il y a une quasi-certitude que le nombre de décès sera compris entre 9 672 et 10 328 morts, donc que D sera égal à 10 000 à 3,3 % près.
Si l’assureur a encaissé 1 000 000 de primes de 1 000 francs, donc 1 000 MF, il peut avoir une quasi-certitude de payer 1 000 MF à 33 MF près, c’est-à-dire à peu de choses près.
La loi des grands nombres ne suffit pas à caractériser l’assurance : il faut ajouter qu’elle fonctionne en capitalisation
L’assurance ayant un rôle (répondre au besoin de sécurité des ménages), il est intéressant de quantifier son importance dans l’économie française.
L’assurance représente-t-elle 1 %, un dixième ou un tiers du PIB français ?
La réponse n’est pas aussi immédiate qu’il y paraît : on peut en effet soutenir que chacun des trois nombres précédents constitue la meilleure réponse.
Commençons par le second nombre, qui est la réponse la plus fréquemment citée. L’assurance ne représente-t-elle pas 10 % du PIB français ? En 1996, le chiffre d’affaires (primes ou cotisations) des sociétés d’assurance, 770 GF, ne représente-t-il pas environ 10 % des 7 861 GF de PIB ?
Mais on peut objecter que le chiffre d’affaires des sociétés d’assurance ne » constitue » pas environ 10 % du PIB, que c’est la valeur ajoutée par l’assurance qui est une part du PIB, et qu’elle en constitue environ 1 % (0,8 %) : à l’appui de ce point de vue, on peut observer que l’assurance emploie environ 200 000 personnes en France, soit 1 Français sur 100 et non 1 sur 10.
Deuxième sorte d’objection à la réponse 10 % : la Sécurité sociale (santé, accidents du travail, retraite) ne répond-elle pas comme l’assurance au besoin de sécurité des ménages ? Les rôles de l’une et de l’autre sont-ils si différents ? Ainsi, lors de la création de la Sécurité sociale en 1947, les accidents du travail qui lui ont été transférés représentaient le tiers du chiffre d’affaires des sociétés d’assurance. De même, l’assurance vie occupe une place plus importante dans les pays anglo-saxons, car les régimes de retraite y sont moins complets. Et si l’on tient compte des prestations, on obtient un chiffre d’affaires total, assurance et Sécurité sociale réunies, qui équivaut à (environ) un tiers du PIB.
Mais si assurance et Sécurité sociale ont un rôle analogue, elles n’ont pas le même mode de fonctionnement.
L’assurance fonctionne en capitalisation. La Sécurité sociale fonctionne en répartition.
Dans un fonctionnement en répartition, les primes reçues dans l’année, voire le mois, servent à payer les sinistres devant être payés dans l’année, voire le mois, même si ces sinistres se rapportent à des périodes de garanties antérieures. Pour payer les sinistres l’année d’après, l’organisme aura besoin de nouvelles primes.
Dans un fonctionnement en capitalisation, les primes reçues au cours d’un exercice donné serviront à payer les sinistres survenus au cours du même exercice. Le paiement des sinistres peut différer de quelques années de l’encaissement des primes.
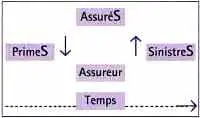Sans entrer dans la comparaison des avantages et inconvénients respectifs des deux modes d’opérer, réécrivons donc le schéma général de l’assurance en tenant compte de son fonctionnement en capitalisation :
Il existe en fait traditionnellement deux modélisations de l’assurance en fonction de la complexité de la prise en compte du temps. Ces deux modélisations différentes définissent deux actuariats différents : un actuariat à court terme utilisé en assurance non-vie et un actuariat à long terme, utilisé en assurance vie.
Cette tradition provient du fait que l’écart temporel entre les primes et les prestations d’un contrat est globalement plus considérable en assurance vie qu’en assurance non-vie. Ceci peut se constater sur les comptes de l’ensemble des sociétés : il s’écoule un an et demi en moyenne en non-vie entre l’encaissement de la prime et le décaissement de la prestation, et cinq à huit ans en vie3.
Une autre différence existe entre les deux actuariats : l’aléa a une place beaucoup moins importante en vie qu’en non-vie.
La raison en est qu’en vie le versement de la prestation dépend le plus souvent de la survie de l’assuré, événement qui a une forte probabilité : sur 10 000 assurés dont une centaine vont mourir dans l’année, quelques dizaines de décès de plus ou de moins sont un aléa négligeable pour l’assureur en cas de survie qui s’attend à payer (environ) 9 900 prestations, et au contraire un aléa important pour l’assureur en cas de décès qui s’attend à payer (environ) 100 sinistres.
Le lecteur attentif, s’il est juriste, s’étonnera peut-être de nous voir prendre l’assurance décès comme exemple d’assurance non-vie. Mais le lecteur hâtif ou sans culture juridique nous pardonnera aisément cette assimilation audacieuse.
Il n’est pas nécessaire à l’assureur de pouvoir appliquer la loi des grands nombres lui-même : il peut se réassurer
La loi des grands nombres, valable pour des risques identiques et indépendants, s’étend aux risques qui à défaut d’être identiques sont homogènes, et à défaut d’être indépendants ne sont pas trop dépendants.
Mais si notre assureur A assure 10 000 assurés pour 100 000 F et se voit proposer un assuré supplémentaire dont la garantie est de 100 MF, il n’est plus vrai qu’il puisse prévoir sa charge sinistre à 33 % près : sa charge de sinistres est devenue de l’ordre soit de 10 MF, soit de 110 MF selon que cet assuré supplémentaire survit ou décède.
Si les risques assurés ne sont pas suffisamment nombreux, homogènes et indépendants pour que l’assureur puisse prévoir correctement la somme des sinistres, en bref, si la loi des grands nombres ne peut pas s’appliquer, l’assureur ne refuse pas de souscrire le risque (et ne refuse pas pour autant la prime) ; simplement, il lui faut se réassurer.
De même, si les assurés, loin de mener leur vie indépendamment l’un de l’autre, font fréquemment des voyages en avion par groupes, la charge des sinistres devient de l’ordre soit de 10 MF soit de l’ordre de 15 MF (voire de l’ordre de 20) selon que l’on suppose que tous les voyages ont été couronnés de succès ou qu’au contraire un avion de 500 assurés s’est écrasé (voire que deux avions se sont écrasés).
Les tempêtes de décembre 1999 ont montré que le marché supportait bien le retour d’un risque qualifié de » centenaire » quelques années seulement après son précédent passage.
La loi des grands nombres concerne très imparfaitement les actifs gérés
La diversification de ces placements est une notion essentielle de la réglementation relative à la solvabilité : il lui est demandé de ne pas » mettre tous ses œufs dans le même panier « , de faire en sorte que la faillite d’une entreprise ou l’écroulement d’un immeuble ne lui coûte pas plus de 5 à 10 % de l’argent des assurés.
La technique de capitalisation qu’il utilise fait de l’assureur un » investisseur institutionnel » : parce qu’il encaisse les primes avant (parfois longtemps avant) d’avoir à décaisser les sinistres, l’assureur dispose de sommes importantes qu’il place.
Mais le risque de marché résiduel n’est pas pour autant justiciable de la loi des grands nombres : il n’est pas vrai qu’en multipliant le nombre d’assurés et donc le montant de ses placements par 100, l’écart type du résultat de l’assureur ne soit multiplié que par 10 : les krachs immobiliers ou boursiers affectent l’ensemble des actifs.
La loi des grands nombres ne suffit pas à éviter la ruine
Revenons aux 10 000 assurés, risques identiques et indépendants, tarifés sur la base d’une probabilité 1 % de décéder dans l’année, pour lesquels A a une quasi-certitude (99,9 % de chances) d’avoir à payer 10 MF à 33 % près.
Si la probabilité de 1 % a été estimée avec précision, mais sur une population différente de celle assurée, et si les assurés ont en réalité une probabilité de décéder égale à 2 %, l’assureur qui s’attendait à payer environ 10 MF devra évidemment payer le double !
Épilogue
Deux problèmes actuariels se posent à l’assureur ex ante (à la souscription d’un ensemble de contrats) :
1) En supposant qu’il ait tarifé parfaitement les risques qu’il assure, son résultat est aléatoire ; que peut-on dire de cet aléa ?
2) Mais le tarif repose sur des estimations : que peut-on dire de l’incertitude découlant de ces estimations ?
Un problème supplémentaire se pose ex post (à l’issue de l’année d’assurance) : que déduire du résultat comptabilisé ? En particulier convient-il de remettre en cause le tarif pratiqué ? Ces problèmes et ces calculs sur le risque de ruine de l’assureur doivent en effet être placés dans le cadre comptable et réglementaire qui traite de ce que l’actuariat appelle la ruine et la réglementation l’insolvabilité.
Dans le premier problème l’assureur prévoit d’autant mieux son résultat (relatif) qu’il a plus d’assurés, puisque s’il multiplie son nombre d’assurés par 100 l’écart type de son résultat n’est multiplié que par 10, à certaines conditions tout au moins.
Dans le second problème au contraire, s’il multiplie son nombre d’assurés par 100 l’impact de son erreur de tarif est multiplié par 100.
Faire des calculs d’assurances en se dispensant de connaître ce cadre revient à jouer au bridge sans savoir comment on compte les points.
_________________________________
1. Adapté de l’ouvrage Assurance : comptabilité, réglementation, actuariat, A. Tosetti, T. Béhar, M. Fromenteau, S. Ménart. (Economica, 2000).
2. Celle-ci dit qu’en multipliant le nombre d’assurés par n, l’écart type du résultat est, dans certaines conditions, multiplié par ÷n . C’est parce qu’ils sont censés comprendre ce que veut dire la phrase précédente que tant de polytechniciens sont recrutés en assurance.
3. Les provisions techniques représentent 1,5 fois les primes en non-vie et 5 fois en vie.
Commentaire
Ajouter un commentaire
Très bon sujet, très
Très bon sujet, très pertinent. Rien à dire