Les mathématiques du réel

Un décalage avant tout culturel
Un décalage avant tout culturel
La recherche en mathématiques, et l’enseignement ne fait que la reproduire, vise avant tout à obtenir des théorèmes : résultats bien démontrés obtenus dans un cadre bien défini. Plus le résultat est difficile et plus le prestige est grand : c’est la technicité qui est le premier critère de jugement. L’enseignement reprend ce critère : nous avons tous appris des théories difficiles (par exemple l’intégration), que nous n’avons que rarement employées ensuite. En partant de bases solides – solides parce qu’axiomatiques – les mathématiques académiques développent des outils extrêmement sophistiqués.
Mais ces outils sophistiqués sont presque toujours inadaptés au monde réel, parce que le cadre axiomatique requis pour leur application n’est pas réalisé en pratique. Le monde réel est fait de données imprécises, fausses, insuffisantes, tronquées. Les contrats que nous traitons sont de nature fondamentale (recherche d’une trajectoire optimale, optimisation d’un réseau, etc.), mais pourtant nous ne trouvons jamais sur les étagères de la recherche académique les outils dont nous aurions besoin : nous devons généralement tout créer nous-mêmes.
Mathématiques et applications
Les mathématiques académiques partent de l’idée que le lien avec les applications se ferait par l’intermédiaire de l’analyse numérique (encore appelée » calcul scientifique »). On commencerait par des théorèmes fondamentaux (portant par exemple sur des solutions au sens » distributions » de telle équation de la physique), puis on résoudrait ces équations, par des méthodes du type discrétisation et maillage (on simplifie les équations en ne considérant les inconnues que tous les mètres, ou toutes les secondes…) ; on traite ensuite par des méthodes informatiques ces problèmes simplifiés et l’ingénieur est tout content : on peut construire une nouvelle machine.
La communauté mathématique française (maths pures et maths appliquées) en est restée à cette description, partiellement vraie il y a plus de quarante ans, devenue totalement fausse aujourd’hui. Les besoins des entreprises ne sont plus en résolution numérique ; les logiciels existants font cela très bien, et les formations de type DESS sont largement surdimensionnées à cet égard.
Les vrais besoins sont de type » modélisation « , ce qui signifie : être capable de poser, en des termes mathématiques, un problème réel. Les étudiants (grandes écoles et université) ne sont absolument pas formés à ce besoin, parce que, comme je l’ai expliqué plus haut, ils ont une approche de type formaliste, alors qu’il faudrait de l’imagination. Sonnent à nos portes des binoclards précautionneux, quand il nous faudrait des barbares.
La modélisation des problèmes réels
Deux difficultés caractérisent les problèmes réels. La première, nous l’avons déjà rencontrée : les données sont insuffisantes. La seconde est pire encore : on ne sait pas ce qu’on veut, ou, plus exactement, on veut tout à la fois.
En théorie, on ne peut optimiser qu’une seule chose à la fois. Certes, cette fonction peut être une somme d’autres fonctions, avec des pondérations, mais le choix de ces pondérations est lui-même arbitraire. Or, dans la pratique, personne n’est satisfait d’une optimisation portant sur un seul critère ; il ne faut pas que les autres contraintes soient ignorées.
Le chef d’entreprise voudrait vendre plus, dépenser moins, satisfaire ses actionnaires, ses salariés, etc. L’ingénieur voudrait que sa machine soit plus précise, dure plus longtemps, pèse moins lourd, coûte moins cher, dépense moins d’énergie, pollue moins. Pour chaque problème que l’on nous soumet, il y a donc un travail très important, et nullement trivial, pour essayer de » faire dire » au client ce dont il a besoin, étant entendu que lui-même, dans nombre de cas, n’en a qu’une idée très générale.
Par exemple, pour optimiser un réseau de distribution d’eau (et obtenir que le débit final soit régulier), il faudra jouer sur des réglages de vannes.
Mais que signifie le mot » débit régulier » ? Quelles variations sont autorisées et comment les mesure-t-on ? Comment les réglages s’opèrent-ils ? Comprendre le problème, c’est à la fois comprendre la question et comprendre les informations disponibles.
Il n’y a rien dans notre enseignement ou notre recherche qui y prépare les étudiants. Bien au contraire, ils auront tendance (c’est bien naturel !) à passer en revue les cours qu’ils ont suivis pour y trouver une idée sur la technique à utiliser. Ils proposeront d’emblée, ici la théorie des jeux, là l’intégrale stochastique. Ils tentent maladroitement de » plaquer » les enseignements qu’ils ont reçus sur la réalité à laquelle ils sont confrontés, mais cette réalité est trop complexe.
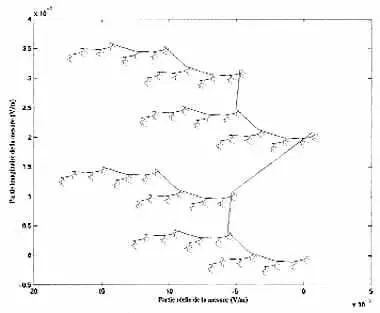
Signal enregistré par une sonde en Courants de Foucault : simulation des différents défauts possibles, en fonction de leur profondeur et de leur localisation dans les tubes des générateurs de vapeur des centrales nucléaires. Travail réalisé par la SCM pour EDF, 1997–2000.
Ce n’est pas seulement que la réalité est trop complexe : l’enseignement serait alors une base, limitée mais sérieuse, qu’il suffirait de compléter. En fait, la réalité est différente. Elle procède systématiquement d’une information incomplète, tant au niveau des données qu’au niveau des besoins, et dans ces conditions l’utilisation d’un outil sophistiqué est inadéquate et absurde. Ce n’est pas une question de niveau : c’est l’orientation fondamentale qui est à revoir.
Je me rappelle un énoncé d’économie, qui postulait que dans telles circonstances on parvenait à un équilibre. Le point de départ était une modélisation d’un ensemble de biens grâce à un espace vectoriel. Mais aucun ensemble de biens n’a réellement de structure additive, et la nature se moque complètement des équilibres.
À quoi servent les mathématiques ?
On en lira des applications spécifiques dans les articles qui suivent. Mais pour nous, à la SCM, elles servent essentiellement à » dimensionner » des systèmes, des outils de production, c’est-à-dire à en déterminer les caractéristiques. Comment leurrer une torpille ? Où mettre une usine ? Comment réguler un réseau ? Voilà des questions qui, pour nous, sont du ressort des mathématiques. Et il s’agit toujours de mathématiques nécessairement grossières, c’est-à-dire comportant une forte part d’incertitude. » Grossier » ne signifie pas simple, bien au contraire.
On entend beaucoup de gens dire : » Je n’utilise que la règle de trois. » Fort bien, lorsque le phénomène en question est linéaire. Mais, dans la nature, les phénomènes sont rarement linéaires sur toute leur échelle : aux deux extrémités, la linéarité disparaît.
Reconnaître ce fait, c’est déjà faire des mathématiques, car on se pose alors la question du domaine de validité de l’approximation.
Remarquons au passage que les mathématiques grossières sont accessibles, pour un étudiant, plus rapidement que les mathématiques académiques : elles sont plus nouvelles et plus attrayantes. Les problèmes posés ne sont pas faciles ; ils sont différents, mais, pour en comprendre l’énoncé, il n’est pas nécessaire d’avoir lu Bourbaki.
En fait, l’outil mathématique, dans ses applications concrètes, reste très largement à créer. Personne ne sait trouver la meilleure route pour un sous-marin, pour lui éviter d’être détecté, sous des contraintes naturelles, ni la meilleure route pour un camion dans ses livraisons, ni le réglage optimal d’un réseau. Ce que l’on a fait jusqu’à présent, c’est tester des théories académiques, développées dans l’abstrait, sur des problèmes concrets : rien d’étonnant que le succès soit rarement au rendez-vous.
Impuissance des mathématiques académiques
Depuis les années soixante-dix, la communauté académique, surtout en France, est très imprégnée de bourbakisme : développer le formalisme et résoudre un certain nombre de questions considérées comme pertinentes par une communauté extrêmement réduite. Cela fait trois générations que les mathématiciens français se sont volontairement coupés des problèmes réels, en décidant eux-mêmes de ce qui était bon pour leur discipline : c’est le principe du » jugement par les pairs » qui prévaut à l’Université.
Il en est résulté ce que von Neumann avait prévu dès 1947 : » la dégénérescence de la profession » tout entière, d’autant que, comme nous l’avons dit plus haut, les liens avec les applications ne sont plus ceux que les universitaires supposent, et l’analyse numérique est devenue d’importance secondaire.
Le remède que proposait von Neumann reste d’actualité : introduire une certaine dose d’empirisme, c’est à dire » se frotter » à la réalité ! Mais ceci est sans doute inconcevable pour la communauté universitaire, pour des raisons de statut qui sont évidentes : le jugement des pairs porte sur la technicité. Pourquoi essayer de réguler un réseau de distribution d’eau alors que :
1) on ne dispose pas des outils mathématiques pertinents pour y parvenir,
2) pour un recrutement ou une promotion, la communauté attend de vous que vous démontriez un théorème ?
La profession de mathématicien a maintenant établi, depuis une trentaine d’années, des critères de recrutement très clairs, et ces critères excluent complètement tout contact avec le monde réel. Un jeune mathématicien, typiquement (c’est ma formation), fera un DEA, puis une thèse en milieu universitaire ; il démontrera des théorèmes, fera des publications, deviendra professeur, aura des thésards, qui démontreront des théorèmes. La quasi-totalité des universitaires n’ont jamais fait le moindre stage en entreprise (leur stage de DEA se réduit à la lecture d’articles et la rédaction d’un mémoire). On n’imagine pas un professeur de médecine qui n’aurait jamais vu de malades, mais, répétons-le, un mathématicien suivant un cursus normal ne voit jamais de problème réel. Le cursus normal est précisément là pour le lui éviter.
Le seul domaine où l’articulation entre la théorie et le réel se fasse correctement, selon mon expérience, est celui des statistiques : les enseignants et les étudiants ont tous rencontré des problèmes réels. Mais, jusqu’à un passé récent, les statistiques étaient elles-mêmes marginales dans la communauté académique.
La nature a horreur du vide
Les mathématiciens du monde académique se sont donc réfugiés, depuis plus de trente ans, dans une bulle aux parois opaques qui les protège du monde extérieur ; ils s’éteignent tranquillement dans ce cocon. En revanche, bien entendu, les problèmes qui se posent aux entreprises, aux politiques, à la société restent à résoudre. Qui donc va les résoudre ?

Analyse du signal sonore. © ECPA/MARINE NATIONALE
La réponse est vague : un peu tout le monde, un peu personne. Ils ne sont pas considérés comme de » vrais » problèmes. Tel responsable logistique » bidouille » sur son tableur Excel pour trouver le meilleur parcours pour ses camions. Telle grande entreprise aéronautique » confie à un stagiaire » (c’est l’expression consacrée) tel problème dont un mathématicien professionnel ne viendrait pas facilement à bout. L’habitude est si ancrée de n’obtenir aucune réponse de la communauté académique qu’on ne lui pose même plus la question.
S’il s’agit d’un problème d’ingénierie (appareils, mécanismes, ouvrages d’art, etc.), sa part purement mathématique est rarement dégagée comme telle par les ingénieurs, qui préfèrent résoudre grossièrement et prendre des coefficients de sécurité. Cette façon de procéder, semi-empirique, est très répandue, et elle est en général légitime.
Dans un problème qui, globalement, est extrêmement complexe, pourquoi s’attacherait-on à une résolution mathématique fine sur un tout petit morceau, qui finalement n’a pas une importance majeure ? Ici, pour que les mathématiques soient efficaces, il faudrait avant tout qu’elles sachent gérer les incertitudes : à quoi bon calculer avec 16 chiffres après la virgule, lorsque les données ne sont connues qu’à 20 % près ? À la différence du mathématicien, qui veut apporter une solution précise à un problème précis, l’ingénieur sait » dimensionner » ses efforts pour que le résultat final prenne en compte toutes les incertitudes.
Pour moi, la découverte de cette évidence date de 1989, à l’occasion du premier contrat qui nous a été confié.
Le donneur d’ordre était un organisme de la Délégation générale pour l’armement, le CAPCA, à Toulon (aujourd’hui : Service des programmes navals) : il s’agissait de trouver des trajectoires optimales d’évasion pour des sous-marins nucléaires (s’enfuir en faisant le moins de bruit possible) en présence d’une menace (un autre sous-marin).
Nous avons élaboré, dans un premier temps, toutes sortes de solutions, dans les espaces de Besov, de Sobolev…, jusqu’à ce que, excédé, je finisse par déclarer à mes collaborateurs : » Un engin de cinq milliards de francs ne navigue pas au sens des distributions. »
Nous avons dû créer les outils adéquats, car il y avait deux difficultés essentielles : la connaissance que l’on a de la menace est imprécise, et le choix de trajectoire doit être robuste, sur plusieurs heures.
Si le problème posé s’inscrit dans le contexte d’une autre discipline, ce sont les chimistes, les physiciens, les automaticiens, les mécaniciens, qui le résoudront eux-mêmes. Pourquoi faire appel à un mathématicien ? Ils considèrent qu’ils sont compétents pour résoudre le problème, qu’ils n’identifient pas comme un problème de mathématiques, mais comme un problème relevant de leur propre discipline.
Mais tirer des conclusions à partir de données, c’est-à-dire réaliser un modèle, requiert tout l’art du mathématicien. C’est un travail de professionnel.
Il en résulte que, dans de très nombreux cas, les déductions réalisées par les spécialistes d’autres disciplines, qui sont des mathématiciens amateurs (sans que ceci soit en quoi que ce soit péjoratif : à chacun son métier) pèchent de manière flagrante. On fait des hypothèses absurdes, des extrapolations grossières. On ignore le sens des concepts probabilistes. On procède par comparaisons injustifiées.
Dans certains domaines, qui ont une importance sociale réelle, des décisions politiques sont prises à partir de modèles non fondés, tirant des conclusions extravagantes à partir de données insuffisantes. Citons pêle-mêle : considérations sanitaires, énergétiques, évolution du climat, etc. Le » dénominateur commun » de toutes ces situations absurdes est que la déduction, le processus intellectuel qui, partant des données, aboutit à la décision, a été réalisée par des personnes insuffisamment formées aux mathématiques : ignorant ce qu’est une analyse de sensibilité et d’incertitude, ignorant de ce que sont les lois du hasard, ignorant ce qu’est la valeur d’une hypothèse, ignorant même, souvent, ce qu’est l’honnêteté intellectuelle. Il s’agit d’aller vite, de recueillir quelques données, de les traiter sur ordinateur, de se faire filmer avec une blouse blanche, de faire peur et, finalement, d’obtenir un budget.
Je ne puis suggérer aucune solution. Il est inutile de demander à la communauté académique de s’intéresser aux problèmes réels : elle n’en a ni le goût ni le talent. Il est inutile de contester au coup par coup les jugements des » experts « , dans tel ou tel domaine : on perd son temps et son énergie ; la presse privilégie le sensationnel et les politiques retiennent surtout ce qui les arrange.
On assiste de plus en plus, malheureusement, à un déclin de l’esprit scientifique, au profit de fausses peurs, de fausses croyances, de dogmes tout faits et socialement acceptés : toutes sortes de sornettes qu’on lit quotidiennement dans les journaux, et qu’il est devenu impossible de remettre en question.
Peut-être la communauté polytechnicienne, qui a compté Henri Poincaré parmi ses membres (mais il est très mort), opposera-t-elle une dernière résistance, sera-t-elle le dernier bastion de l’esprit scientifique ? J’aimerais le croire…
J’ai demandé leur avis, sur les problèmes que je viens d’évoquer, à sept spécialistes de domaines très divers. On lira ci-après leurs points de vue. Bien entendu, ils ont été écrits en toute indépendance et sans aucune concertation préalable : chacun d’eux a écrit ce qu’il a voulu. Mes vifs remerciements à DCN pour les photos de sonar et de radar, qui constituent des illustrations particulièrement appropriées pour les » mathématiques du réel « .