Les métamatériaux en mécanique
Au cours des vingt dernières années, de nouveaux matériaux sont sortis des laboratoires universitaires. Possédant des propriétés électromagnétiques, acoustiques, mécaniques et thermiques que l’on ne rencontre pas dans la nature, ils ont été qualifiés de métamatériaux (méta signifiant au-delà en grec). Parmi ces propriétés extraordinaires, celle qui à ce jour a le plus frappé l’esprit du grand public est sans nul doute celle, baptisée « cape d’invisibilité », relative à la propagation des ondes électromagnétiques.
On peut relever quelques applications à la mécanique du principe de la cape d’invisibilité. L’idée générale est que, en utilisant différents matériaux ayant des forts contrastes de propriétés et en jouant sur leur agencement géométrique, on peut obtenir des propriétés effectives que l’on n’observe pas dans la nature sur les matériaux réels. L’origine de ce comportement « anormal » peut être simplement statique, mais les propriétés les plus originales sont obtenues en dynamique en s’appuyant sur le phénomène de résonance. Les paragraphes qui suivent vont l’illustrer.
REPÈRES
Le principe de la « cape d’invisibilité » est le suivant : en arrangeant astucieusement dans une région de l’espace des hétérogénéités (de petite taille), les ondes seront déviées, contourneront l’obstacle et rendront invisible à un observateur extérieur cette région de l’espace. On voit immédiatement toutes les applications que l’on pourrait tirer de ce phénomène. Cette propriété n’est pas spécifique aux ondes électromagnétiques, mais peut se généraliser à tout phénomène ondulatoire. D’où par exemple l’idée de l’Institut Fresnel de fabriquer des amortisseurs de houle en disposant des piliers sur des couronnes concentriques. Ici il s’agit de protéger la région centrale des effets de la houle, les piliers servant de déviateurs.
Les matériaux auxétiques
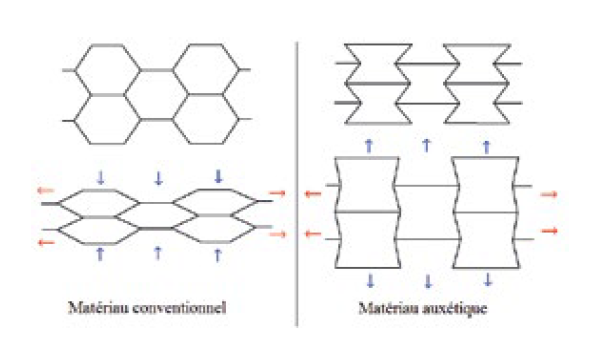
Rappelons que, mis en évidence (analytiquement) par Siméon Denis Poisson, le coefficient dit de Poisson permet de caractériser la contraction de la matière perpendiculairement à la direction de l’effort appliqué. Les matériaux traditionnels ont un coefficient de Poisson positif : quand on les étire dans une direction, ils se contractent dans les directions transverses. De la même façon, si on fabrique une structure composite en disposant un matériau en nid‑d’abeilles, le comportement effectif obtenu correspondra à un matériau avec coefficient positif. En revanche, si le matériau de base est disposé suivant des cellules réentrantes (c’est-à-dire concaves), alors on obtient un matériau effectif auxétique, c’est-à-dire à coefficient de Poisson négatif.
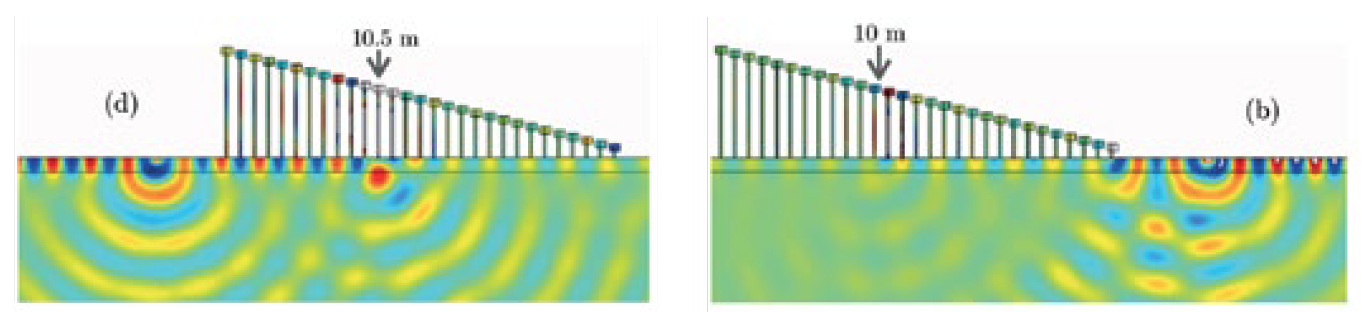
La conversion d’ondes par une forêt d’arbres
On envisage aujourd’hui de protéger certains sites sensibles des risques sismiques en plantant une forêt d’arbres de hauteur variable. On s’appuie pour cela sur le fait que les arbres vont modifier la propagation des ondes guidées (Love) ou de surface (Rayleigh) en créant des conditions aux limites effectives à la surface du sol différentes des conditions de bord libre usuelles en l’absence d’arbres. La théorie, étayée par la simulation numérique, montre qu’une onde incidente de surface peut être entièrement réfléchie ou convertie en onde de volume lorsque la fréquence d’excitation correspond à une fréquence propre de vibration d’une rangée d’arbres, par simple effet de résonance. Ces résultats théoriques fondamentaux intéressent évidemment le génie parasismique. Il reste à vérifier la faisabilité du système en vraie grandeur.
de Poisson positif.
La récupération d’énergie par résonance locale
En utilisant des matériaux élastiques à fort contraste de rigidité, on peut obtenir un matériau dont la masse effective en dynamique devient négative à certaines fréquences. C’est le cas par exemple d’une matrice raide comportant un réseau périodique d’inclusions très molles. On montre, par un calcul explicite utilisant des techniques asymptotiques, que du fait d’un phénomène de résonance locale des inclusions la masse effective de ce composite est négative dans certaines bandes de fréquence. De ce fait les ondes élastiques ne pourront pas se propager dans le composite à ces fréquences-là, qui constituent donc des bandes interdites.
Cette propriété peut être utilisée pour concentrer de l’énergie dans une zone prédéfinie d’un microsystème comme l’illustre l’exemple suivant : on insère deux bandes de largeur l d’un métamatériau composite dans la matrice, en les espaçant d’une distance 2d. Si l’on envoie un signal à une fréquence correspondant à une fréquence interdite du métamatériau, alors on peut obtenir une transmission totale dans la partie droite, pourvu que l’espacement d soit convenablement choisi. De plus, l’amplitude du signal dans la partie centrale de la matrice sera considérablement amplifiée. On a donc concentré de l’énergie dans la partie centrale. Ce phénomène est analogue à l’effet tunnel en mécanique quantique. Il s’explique par les divers effets de résonance qui sont présents dans cette situation (dans les métamatériaux et dans la partie centrale).
Des perspectives stimulantes
Les métamatériaux ouvrent donc de formidables perspectives du point de vue des applications. Ils constituent également un grand défi tant scientifique que technologique. D’un point de vue scientifique, il s’agit de mieux comprendre les phénomènes qui conduisent à ces comportements extraordinaires, de bien identifier les microstructures susceptibles de les provoquer et de construire des modèles prédictifs capables d’en rendre compte. Du point de vue technologique, il s’agira d’être capable de fabriquer à grandes échelles ces matériaux microstructurés et de valider sur le terrain leurs performances pressenties.
Retrouvez l’ensemble du dossier : La mécanique
Articles similaires :
Histoire de l’enseignement de la mécanique à l’École polytechnique
L’histoire des industries mécaniques
La mécanique à l’Ecole polytechnique
Les mécaniciens français à l’international
Une révolution : le traitement thermique
La recherche à l’X : nanosciences, matériaux innovants et procédés efficaces