La modélisation du comportement des polymères, aide à l’innovation

Le laboratoire de mécanique des solides (LMS) conjointement avec le laboratoire de mathématiques appliquées (CMAP) travaille actuellement avec la société Arkema, dans le cadre d’une chaire industrielle, à définir les outils mathématiques décrivant au mieux le comportement des matériaux pour proposer des applications extrêmement variées. La collaboration du premier chimiste français et de mathématiciens et mécaniciens académiques est la preuve de la pluridisciplinarité actuelle de la recherche en matériaux et de l’utilité de cette recherche pour la société.
On s’intéressera ici à la mécanique des matériaux polymères. Le mécanicien des matériaux se concentre notamment sur la relation entre microstructures et propriétés mécaniques. Si la cause physique de cette relation questionne, le but principal n’est pas d’en donner une explication, qui parfois d’ailleurs nous échappe, mais de proposer des lois de comportement tridimensionnelles, au moins descriptives et possiblement prédictives, qui soient utiles à l’ingénieur pour le dimensionnement, la tenue en service ou la durée de vie d’ouvrages, de structures… Par conséquent, le travail associe un effort de caractérisation expérimentale du comportement mécanique et de la microstructure, et un effort de modélisation à l’échelle macroscopique.
REPÈRES
Dans le langage commun, les polymères incluent les plastiques, caoutchoucs, résines… Si l’image de ces matériaux est actuellement dégradée auprès du grand public pour des raisons écologiques évidentes, ils permettent pourtant de réduire la consommation d’énergie, du fait notamment de l’allègement des structures. On les retrouve aussi bien dans les transports ou dans l’énergie (flexible offshore, pale d’éolienne, capteur piézoélectrique ou électroactif) que dans les loisirs (chaussures et appareils de sport)… Le développement de polymères biodégradables ou écoresponsables est déjà largement avancé et les nouveaux procédés tels que l’impression 3D permettent la fabrication de matériaux architecturés plus performants, tout en minimisant la consommation de matière.
Des lois de comportement originales…
Pour optimiser l’utilisation des polymères, on a besoin de lois de comportement. Or le comportement des polymères change drastiquement en fonction de la température ; ils passent d’un comportement de type plastique à froid à un comportement de type caoutchouc à chaud, c’est-à-dire au-delà de leur température de « transition vitreuse ». Selon le polymère, la température de transition vitreuse peut descendre à – 70 °C ou dépasser 200 °C. Par ailleurs, les polymères amorphes et certains polymères semi-cristallins présentent deux propriétés intéressantes que sont la viscoélasticité et l’équivalence temps-température.
Pour expliquer simplement ces deux propriétés, on peut dire que la réponse de ces matériaux ne dépend pas seulement du chargement mais de tout son historique, et que l’espace-temps, défini à température ambiante, se contracte aux basses températures et s’étend aux températures élevées. Une expression simple de la combinaison de ces deux propriétés est la mémoire de forme des réseaux amorphes. Si les physiciens des polymères ont rapidement compris que la mobilité réduite à froid des chaînes polymères permettait de retenir la forme temporaire, alors que l’activation thermique des chaînes à chaud assurait le retour de forme, nous avons démontré que la simple prise en compte de ces deux propriétés intrinsèques permettait d’écrire les équations mathématiques utiles à prédire la cinétique de mémoire de forme.
Ces équations ont par ailleurs d’autres applications, comme celle de prévoir le rebond d’une balle en fonction de sa température. On peut observer qu’un joueur de squash à l’échauffement frappe fort dans sa balle pour en élever la température et ainsi en améliorer le rebond. En effet, en augmentant la température de la balle, on s’éloigne du domaine visqueux, réduisant ainsi la part d’énergie dissipée par viscoélasticité pendant le rebond. La performance au rebond de la balle en fonction de la température peut être prédite avec la même loi de comportement que celle utilisée pour la mémoire de forme.
La mémoire de forme des réseaux amorphes
À chaud (au-delà de leur température de transition vitreuse), les réseaux polymères peuvent se déformer facilement et de façon réversible, comme un élastique. Si un changement de forme est appliqué à chaud et maintenu pendant le refroidissement (en dessous de la température de transition vitreuse), la forme temporaire pourra être conservée à froid sans effort et cela aussi longtemps qu’on le souhaite. En revanche, un simple chauffage permet au matériau de retrouver sa forme initiale.

Un équipement de pointe
Les paramètres microstructuraux déterminant le comportement d’un polymère peuvent être à l’échelle des chaînes macromoléculaires. Pour les polymères semi-cristallins, le taux de cristallinité, la maille cristalline et l’arrangement des cristallites ont un impact sur leur comportement. Selon le procédé de mise en œuvre choisi, une structure à l’échelle supérieure, appelée mésostructure, peut être créée, par exemple pour les mousses. Dans le cas d’une mousse, la densité de matière, la distribution des tailles des cavités, le fait que ces dernières soient ouvertes ou fermées, sont à prendre en compte. Au laboratoire de mécanique des solides, nous bénéficions de nombreux appareils de caractérisation des matériaux, tels que microscope électronique à balayage, microscope à force atomique et calorimétrie à balayage différentiel. Connaître la microstructure du matériau d’intérêt à toutes les échelles permet d’identifier les paramètres pilotant son comportement et son endommagement.
Il est également possible d’ajouter des inclusions (charges) aux polymères. Ces charges peuvent contribuer aux propriétés mécaniques, comme à la résistance à l’usure dans le cas des élastomères chargés en noir de carbone, à la réduction de l’apparition de fissures dans le cas des polyméthacrylates de méthyle chocs, aux propriétés fonctionnelles comme la propulsion solide des propergols, ou encore au couplage multiphysique d’élastomères magnétorhéologiques.
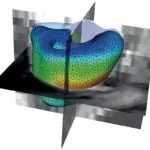
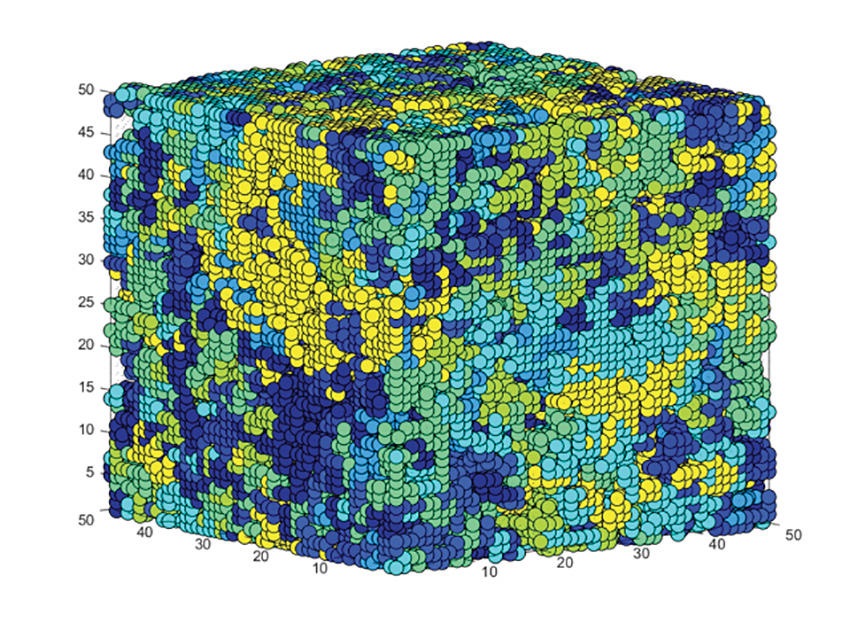
La nature, la quantité, l’organisation de ces charges ont un impact sur le comportement ou l’endommagement des polymères. Pour prédire cet impact, nous pouvons avoir recours à une modélisation à transition d’échelle qui permet de calculer, à partir d’une microstructure hétérogène, le comportement du matériau homogène équivalent, soit un matériau homogène virtuel qui a le même comportement que le matériau hétérogène. Cette modélisation permet de mieux apprécier le rôle des paramètres microstructuraux sur les propriétés macroscopiques, mais – plus intéressant – elle peut devenir un outil pour définir les microstructures pertinentes en fonction des applications visées.
Retrouvez l’ensemble du dossier : La mécanique