Modélisation et simulation en ingénierie et sciences physiques
Le travail de simulation exige de prendre de grandes précautions. Ce n’est pas une action « presse-bouton » qui permet de brandir ensuite avec une confiance aveugle de belles images de résultats. On doit s’assurer à chaque fois du respect des exigences scientifiques et de la maîtrise du niveau d’erreur et d’incertitude.
Un nouveau marché se dessine en ingénierie, concentré autour de quelques grands éditeurs de logiciels (Ansys, Nastran, Abaqus) omniprésents et des sociétés de services assurant l’interfaçage avec les besoins des différents bureaux d’études.
Une société comme Simulia créateur d’Abaqus, fondée en 1977 par Dave Hibbitt et rachetée par Dassault Systèmes en 2005, a un chiffre d’affaires de plusieurs centaines de millions d’euros dans un marché mondial estimé par CIMdata et par de nombreux analystes à plus de 5 milliards de dollars.
De même, dans les grands domaines scientifiques (météorologie, chimie), il existe des logiciels de référence soit commerciaux soit libres d’accès et développés par des laboratoires publics internationaux (VASP pour la chimie quantique, LAMMPS en dynamique moléculaire).
REPÈRES
Tous les domaines d’activité sont concernés par la simulation. On simule ainsi le fonctionnement en roulage nominal ou extrême d’un pneumatique, l’environnement acoustique d’une automobile, des amerrissages d’avion de ligne, la diffusion grande échelle d’une pollution aérienne, des comportements accidentels de réacteurs nucléaires, l’effet potentiel d’un incendie dans un bâtiment, la résistance au choc d’un téléphone portable, le comportement local d’une microsoudure dans un circuit électronique. On assiste aussi à un développement récent vers la microélectronique de masse.
GAINS DE TEMPS ET D’ARGENT
La simulation ouvre de nouveaux horizons : concevoir plus vite, mieux valider les domaines d’utilisation des produits, réduire les essais, tester de nouveaux concepts, mieux comprendre le fonctionnement en ayant accès à des informations inaccessibles (situées à l’intérieur de l’objet ou observables à des échelles submicroniques ou kilométriques difficiles d’accès), étudier des situations accidentelles ou des utilisations en mode hostile inaccessibles à l’expérience.
“ L’absence de modèle sous-jacent empêche une validation scientifique des résultats obtenus ”
Dans cet environnement, l’ingénieur peut-il maintenant se contenter d’un travail de mise en données de son problème, avant de cliquer pour obtenir son résultat, et de le visualiser sous la forme de belles images ou vidéos en couleur ?
De manière plus générale, que cachent les belles images de simulation ? Quelles techniques mobilisent-elles ? À quoi nous donnent-elles accès ? Peut-on leur faire confiance ? Quels sont les axes de développement ?
UNE GRANDE EXIGENCE SCIENTIFIQUE
La première leçon de trente années de simulations à grande échelle est le respect des exigences scientifiques.
Elles nécessitent un fondement physique, un cadre mathématique précis, l’accès à des données expérimentales permettant de paramétrer et valider le modèle, mais aussi une complexité maîtrisée, et la capacité à transformer des algorithmes en outil de simulation par prise en compte des contraintes et détails technologiques (qui dépendent des applications et des métiers).
ALLUMAGE CIRCULAIRE D’UNE CHAMBRE DE COMBUSTION ANNULAIRE
© LABORATOIRE EM2C, ÉCOLE CENTRALE SUPÉLEC
Le système désigné sous le nom de MICCA est constitué d’un foyer annulaire muni de parois latérales cylindriques en quartz permettant un accès optique à la zone de combustion. Le fond de chambre est équipé de 16 injecteurs comportant chacun une vrille. Les injecteurs sont alimentés par un mélange d’air et de propane.
Les colonnes 1 et 3 montrent des instantanés de l’émission de lumière de la flamme, représentative de l’intensité de la réaction (le niveau d’intensité est représenté sur une gamme de couleurs allant du brun au jaune clair). Ces images donnent la position de la flamme au cours de l’allumage circulaire (light-round).
Les colonnes 2 et 4 donnent les résultats de calculs réalisés par simulation des grandes échelles (Large Eddy Simulation). La flamme est représentée par une isosurface de température colorée par la vitesse axiale. Le code AVBP du Cerfacs et d’IFPEN est utilisé pour ces simulations. Le système est discrétisé sur 55 millions de nœuds correspondant à 310 millions de mailles. Le calcul demande 1 million d’heures (plus d’un siècle) et il est réalisé en parallèle en quelques mois sur 6 000 processeurs.
DES MODÈLES CONFORMES AUX LOIS DE LA PHYSIQUE
L’objectif est de simuler le réel, il faut donc d’abord en avoir un modèle, sous forme d’équations (lois de bilan et/ou équations aux dérivées partielles) qui transcrivent les grandes lois de conservation physique (masse, quantité de mouvement, énergie, entropie) et qui prennent en compte les comportements réels des matériaux.
“ Le grand danger est de faire une confiance aveugle aux résultats obtenus ”
À défaut, la simulation est limitée à un domaine étroit d’utilisation validé après un fastidieux calibrage, et qui devient caduque dès que les paramètres de la simulation changent. Par ailleurs, l’absence de modèle sous-jacent empêche une validation scientifique des résultats obtenus.
L’activité de recherche sur le développement de modèles adaptés a été particulièrement féconde les trente dernières années, avec par exemple en mécanique une prise en compte de phénomènes clés comme la plasticité, la fatigue, l’endommagement, les effets de température, la turbulence, la combustion.
DES TECHNIQUES MATHÉMATIQUEMENT FONDÉES
Les techniques de simulation s’appuient aussi sur de grandes techniques numériques qui ont été introduites et développées dans les cinquante dernières années et qui sont indispensables à leur mise en œuvre : méthode des éléments finis, des différences finies, des volumes finis, méthodes particulaires…
Un ingénieur peut-il se contenter de travailler sur son ordinateur ?
© GOODLUZ
Ces techniques travaillent sur un même principe de base : une multitude (plusieurs millions, voire quelques milliards) d’agents en interaction qui effectuent des opérations simples. Il s’agit d’une écriture locale du principe des puissances virtuelles sur un grand nombre de géométries élémentaires pour la méthode des éléments finis, de la vérification en un grand nombre de points de discrétisation d’une équation aux dérivées partielles pour la méthode des différences finies, de l’écriture de lois de bilan sur des millions de volumes de contrôle pour les volumes finis, d’intégration élémentaire sur des millions de particules des lois de la dynamique du point avec simulation déterministe ou aléatoire des collisions pour les méthodes particulaires.
Un cadre mathématique adapté est nécessaire pour démontrer le passage à la limite quand le nombre d’agents augmente, pour garantir la stabilité du calcul (robustesse aux bruits, aux imprécisions numériques ou aux erreurs de données) et pour améliorer l’efficacité (réduire le nombre d’opérations ou le temps de calcul sur une architecture donnée) à niveau de qualité égale.
C’est le domaine du calcul scientifique et de l’analyse numérique. Pour être efficace, il faut disposer d’un tel cadre, savoir gérer la discrétisation (à savoir le nombre et la localisation des instants physiques et des points en espace utilisés dans les simulations), avoir à disposition des algorithmes robustes et rapides d’algèbre linéaire afin d’effectuer les nombreuses opérations matricielles rencontrées.
NOUVELLES APPROCHES
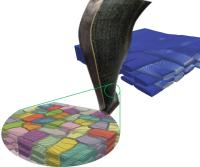CALCUL MULTIÉCHELLES D’UNE STRUCTURE COMPOSITE TISSÉE
Dans cet exemple, il y a prise en compte en chaque point du comportement mécanique élémentaire de chacune des mèches du tissu et leurs interactions locales — Safran Group Simulation.
Les progrès récents de l’analyse numérique ont permis de développer des techniques de maillage adaptatif, de meilleurs solveurs non linéaires, des méthodes de décomposition de domaines permettant de réduire la taille et de paralléliser les calculs.
Cela permet de réduire le nombre d’inconnues nécessaires à la solution du problème (plusieurs millions d’inconnues à identifier sur plusieurs milliers de pas de temps) et d’obtenir une solution avec un nombre d’opérations élémentaires proportionnel au nombre d’inconnues et non pas au nombre d’inconnues au carré comme on peut l’obtenir avec des approches plus naïves.
L’INDISPENSABLE MAÎTRISE DES RÉSULTATS
Reste à savoir maîtriser le niveau d’erreur et d’incertitude dans les résultats obtenus. Il s’agit d’un point clé des simulations actuelles. Le grand danger avec les nouvelles techniques de conception est de faire une confiance aveugle aux résultats obtenus.
Erreurs ou imprécisions dans les données ou hypothèses tacites inappropriées peuvent considérablement fausser le résultat. Les accidents industriels majeurs sont ainsi souvent liés à des analyses de fonctionnement ou de sûreté s’appuyant sur des simulations mal validées.
Citons par exemple le naufrage de la plateforme Deepwater Horizon au Texas ou l’effondrement du terminal 2E à Roissy. Pour surmonter ces dangers, il est possible de s’appuyer sur des techniques de calculs d’erreur et d’incertitude, mais celles-ci sont encore en développement, et ne sont pas disponibles en exploitation.
De plus, elles ne remplaceront jamais l’art de l’ingénieur pour détecter les incohérences de modèle ou de résultats. L’ingénieur moderne doit savoir valider un résultat ou remettre en cause les nombreuses hypothèses et approximations sous-jacentes à sa modélisation.
La simulation sur des sujets critiques doit aussi se confronter à des essais en petit nombre, mais pertinents et bien maîtrisés.
DE NOUVELLES FRONTIÈRES
Où sont les enjeux du futur dans un paysage où nous pouvons disposer de modèles pertinents, de techniques numériques efficaces, de logiciels de simulation de qualité industrielle, d’interfaces métiers ? Nous venons de voir une première frontière : savoir garder la maîtrise de sa simulation et évaluer sa pertinence et sa qualité.
“ Les simulations doivent marier des modèles à grande échelle et des modèles à petite échelle ”
La deuxième concerne les simulations multiéchelles ou multiphysiques. Dans de nombreuses applications critiques, le comportement global du système est fortement influencé par les phénomènes mis en jeu à petite échelle, phénomènes qui peuvent coupler divers domaines scientifiques : c’est le cas de la turbulence en aérodynamique ou en météorologie, c’est aussi le cas en science des matériaux où il est nécessaire de maîtriser la microstructure du matériau (du nanomètre au micron) pour obtenir un matériau performant et durable, ou pour lui donner des fonctions nouvelles.
Dans ces deux situations, les simulations doivent marier des modèles à grande échelle et des modèles à petite échelle.
On doit alors s’appuyer sur des techniques nouvelles telles les Large Eddy Simulations (LES) en mécanique des fluides, les techniques d’homogénéisation en mécanique des solides ou en électromagnétique des milieux denses, et savoir maîtriser des couplages forts entre ondes et matière par exemple.
CONFRONTER SIMULATIONS ET OBSERVATIONS
Une dernière frontière particulièrement importante concerne enfin le dialogue essais-calculs et plus généralement la maîtrise des échanges entre simulation et observation. Les techniques de calcul ont considérablement évolué en trente ans.
Il en est de même des observations, avec le développement systématique des observations à différentes échelles et du traitement d’image.
La vélocimétrie laser, le développement des caméras rapides, les observations sous microscope électronique de matériaux soumis à chargement, les essais sous rayons X, sous caméra infrarouge ou sous tomographe permettent de mesurer des champs de vitesse, de déformation ou de température en tout point de l’espace, qu’il est alors possible de confronter ou de coupler au calcul (encadré ci-dessous) soit pour identifier des paramètres inconnus, soit pour valider des résultats de simulation.
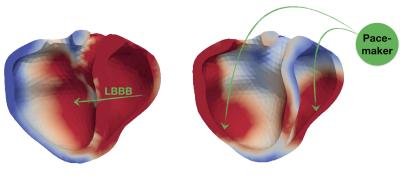CALCUL PRÉDICTIF
