Pour une résolution simple de la conjecture de Kepler (Le dix-huitième problème de Hilbert)
PDF de l'articleLa conjecture de Kepler
|
Deux couches successives du rangement “hexagonal compact” |
La conjecture de Kepler
|
Deux couches successives du rangement “hexagonal compact” |
« Combien de boulets de canon peut-on ranger dans un espace donné ? », telle est la question que Sir Walter Raleigh, navigateur et explorateur britannique du xvie siècle, pose à son ami le mathématicien et astronome Thomas Harriot. La question n’est pas gratuite : quand on range les boulets l’un après l’autre, au hasard, ils ne remplissent que 62 à 65 % de l’espace disponible, tandis qu’un rangement soigneux permet de dépasser 70 %. Ceci peut être la différence entre victoire et défaite dans une bataille navale…
Thomas Harriot transmettra la question à Kepler qui répondra qu’à son avis les rangements les plus compacts sont le rangement « cubique à faces centrées » et le rangement « hexagonal compact » équivalent (figure 1). Ils permettent d’atteindre 74,048 % de l’espace disponible (soit Pi/181/2). Ce résultat est admis depuis longtemps par les physiciens et les chimistes, mais l’absence de démonstration complète a longtemps tourmenté les mathématiciens. C’est une question difficile : il faut considérer tous les rangements possibles, certains sont plus compacts que ceux de Kepler sur de petits volumes, mais très vite ils obligent à laisser des trous.
Le premier résultat important est dû à Gauss en 1831 : « Parmi les réseaux réguliers (où chaque sphère est entourée de la même façon par ses voisines), ceux de Kepler sont les plus compacts. » Puis Voronoï définira les « cellules de Voronoï » (figure 2), c’est-à-dire l’ensemble des points entourant une sphère donnée et situés plus près d’elle que des autres sphères voisines, Delaunay définira les éléments conjugués des cellules de Voronoï.
En 1953, le Hongrois Laszlo Fejes Toth montre la possibilité de construire une fonction dont le minimum indiquera, ou non, si la conjecture de Kepler est juste. Il émet aussi une autre conjecture : « La plus petite cellule de Voronoï est le dodécaèdre régulier circonscrit à la sphère étudiée » (figure 3). Cette conjecture est démontrée en 1998 par Sean Mac Laughin et comme la sphère occupe 75,47 % du volume du dodécaèdre circonscrit on obtient ainsi un majorant du coefficient de remplissage. Ce majorant est très proche des 74,048 % de Kepler ce qui fait que la conjecture est dès lors presque démontrée.
Thomas C. Hales construit la fonction de L. F. Toth en 1998 et présente une démonstration de la conjecture de Kepler, mais sa démonstration comporte 250 pages (réduite à 121 pages en 2005) et s’appuie sur des calculs numériques utilisant 3 gigabits…
Rendue prudente par les différents échecs qui ont ponctué l’étude de la conjecture de Kepler, la communauté mathématique confie à douze spécialistes particulièrement qualifiés le soin d’examiner le travail de Thomas C. Hales. Ceux-ci, après quatre années d’examen, concluent : « Nous sommes à 99 % sûrs de la validité de cette démonstration… »
Une simplification n’est pas superflue !
Une extension des cellules de Voronoï
Considérons un ensemble de sphères égales et non sécantes.
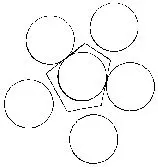 Un rangement quelconque, une sphère centrale et sa “cellule de Voronoï” |
Plaçons l’origine O en l’un de ces centres et étudions la cellule de Voronoï correspondante. Si a, b, c sont les cordonnées du centre d’une sphère voisine, un point x, y, z de la cellule de Voronoï vérifiera :
x2 + y2 + z2 < (x — a)2 + (y — b)2 + (z — c)2 (1)
soit : 2(ax + by + cz) < a2 + b2 + c2 (2)
La cellule de Voronoï est l’ensemble des points x, y, z vérifiant (2) pour toutes les sphères voisines, elle est limitée par des faces planes, c’est donc un polyèdre convexe.
Nous appellerons V1 le volume de la cellule de Voronoï, il vaut 0,693 786… pour un dodécaèdre circonscrit et 0,51/2 = 0,707 106… pour les sphères des réseaux de Kepler.
Pour étendre la notion de cellule de Voronoï, appelons « cellule de Voronoï d’ordre 2 » l’ensemble des points x, y, z pour lesquels l’origine O étudiée n’est plus le centre le plus proche, mais reste tout de même le deuxième centre le plus proche. Donc les coordonnées x, y, z des points de la cellule de Voronoï d’ordre 2 seront définies par la satisfaction de toutes les inéquations (2) sauf une. Cette deuxième cellule est composée de n polyèdres convexes entourant la première cellule le long de ses n faces.
Appelons V2 le volume de la cellule de Voronoï d’ordre 2. On vérifie que V2 vaut encore 0,51/2 pour les sphères des réseaux de Kepler et est compris entre 0,841 189… et 0,857 567… si la première cellule est un dodécaèdre circonscrit (selon la position des sphères extérieures aux douze sphères en icosaèdre régulier tangentes à la sphère initiale).
Les réseaux de Kepler ne correspondent ni au minimum de V1, ni au minimum de V2, mais, et c’est là le point décisif, ils correspondent apparemment au minimum Sm de la somme S = kV1 + (1 — k)V2 lorsque le paramètre k est compris entre 0,3 et 0,85 ; ce minimum vaudrait alors Sm = V1 = V2 = 0,51/2. Ainsi en attribuant chaque « millimètre cube » de l’espace aux deux sphères les plus proches, dans la proportion k à la première et (1 — k) à la seconde, on fait correspondre à chaque sphère un volume qui est au moins Sm et qui est entièrement disjoint des volumes attribués aux autres sphères. Mais le volume de chaque sphère est Pi/6, le cœfficient de remplissage d’un rangement quelconque ne peut dès lors dépasser le rapport Pi/6Sm, soit donc Pi/181/2 si l’on a bien Sm = 0,51/2. Or Pi/181/2 est précisément la limite donnée par Kepler, sa conjecture serait dès lors démontrée.
Il nous faut donc, pour une sphère donnée, étudier les volumes V1 et V2 possibles selon les divers rangements et rechercher le minimum Sm de la somme S = kV1 + (1 — k)V2.
Étude de la somme S = kV1 + (1 — k)V2, et de son minimum absolu Sm
Appelons C la sphère étudiée dont le centre est à l’origine des coordonnées et le diamètre 1, et soient V1 et V2 les volumes de ses deux cellules correspondantes. L’étude de ces volumes ne peut guère se faire analytiquement et doit donc être complétée numériquement.
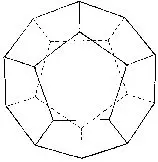 Le dodécaèdre régulier |
Fort heureusement c’est une étude numérique d’une grande simplicité, une optimisation paramétrique ordinaire beaucoup plus simple que l’étude numérique correspondante de Thomas Hales, et qui a aussi l’avantage d’être « finie » : le nombre des paramètres à mettre en jeu est très limité.
Il est en effet tout à fait suffisant de ne considérer que les parties de V1 et V2 situées à l’intérieur de la sphère « U », la sphère « unité » d’équation : x2 + y2 + z2 < 1 (donc deux fois plus large que la sphère C et les sphères du rangement étudié). Cela ne peut augmenter ni S ni Sm et ne nécessite que l’étude des positions des sphères voisines dont les centres sont à moins de deux unités de l’origine (avec utilisation des équations (2) correspondantes).
On constate au passage que :
a) pour les réseaux de Kepler les volumes V1 et V2 sont entièrement à l’intérieur de la sphère U ;
b) pour les rangements intéressants le volume V1 est toujours entièrement dans la sphère U — ce qui est aisé à démontrer — et le volume V2 n’en dépasse qu’exceptionnellement et toujours pour une quantité minuscule.
Pour que Sm puisse être égal à 0,51/2, il faut bien sûr qu’existe au moins une valeur favorable du paramètre k et, puisque S = kV1 + (1 — k)V2 entraîne k = (S — V2)/(V1 — V2), ces valeurs favorables sont limitées par les conditions suivantes :
lim inf k = lim sup pour V1 > V2 de [(0,51/2 — V2)/(V1 — V2)] (3)
lim sup k = lim inf pour V2 > V1 de [(V2 - 0,51/2)/(V2 — V1)] (4)
Il nous suffit bien sûr que lim sup k ≥ lim inf k et pour l’instant les recherches, tant analytiques que numériques, effectuées d’abord un peu au hasard, puis au flair dans les directions les plus prometteuses ont donné les résultats suivants :
. pour V2 > V1 et la recherche de lim sup k, les cas intéressants sont ceux avec V1 < 0,51/2. L’étude analytique, avec minimisation de V1 et V2 , montre qu’il faut alors avoir une première couronne de douze sphères tangentes à la sphère C et l’étude numérique complémentaire conduit déjà au résultat suivant très suffisant pour la présente étude :
0,85 < lim sup k < 0,909 (5)
. pour V1 > V2 et la recherche de lim inf k, le meilleur résultat connu est obtenu avec une première couronne de 14 sphères dont les centres sont aux points suivants :
(± a, 0, 0) ; (0, ± a, 0) ; (0, 0, ± a) ; (± b, ± b, ± b) (6)
avec : a = 1,036 046… ; b = 0,653 248… ; a2 — 2ab + 3b2 = 1 (7)
La dernière égalité est liée à la condition : distance entre centres de sphères voisines ≥ 1.
Ce rangement conduit à :
V1 = 4,5 b3 — 0,5(3b — a)3 = 0,860 373… ; V2 = 4,5(2b — a)3 + 0,5 a3 = 0,645 058… (8)
ce qui donne donc le minorant suivant de lim inf k : (0,51/2 — V2)/(V1 — V2) = 0,288 176… (9)
On voit combien grande est la marge restante, surtout si l’on sait que ce dernier résultat correspond à une exploration numérique fouillée et qu’il est très vraisemblable qu’il ne puisse plus être amélioré que de quelques pour cent… Si tant est qu’il puisse encore être amélioré !
Conclusion
Une méthode nouvelle, d’une grande simplicité, permet d’attaquer la quadricentenaire conjecture de Kepler avec la quasi-certitude du succès. Il reste certes à vérifier ou au moins à estimer numériquement la limite inférieure du paramètre k, mais la marge restante est si grande qu’il n’y a plus guère de doute sur le résultat final. J’invite tous les numériciens à se lancer dans ce programme comme l’ont déjà commencé mes amis ci-dessous remerciés.
Remerciements et dédicace
Je remercie Madame Françoise Montigny et Monsieur Georges Hoynant qui se sont lancés avec enthousiasme et succès dans les études numériques indispensables lesquelles ont beaucoup clarifié cette question et vont très certainement mener au succès.
Je dédie ce travail à mon père Jacques Marchal (33) qui était un passionné des polyèdres. Il les a étudiés, classés, dessinés et même fabriqués pendant des décennies, ce qui m’a été très utile pour cette étude.
Articles similaires :
L’opinion des polytechniciens sur le problème de l’emploi. Compte rendu d’une enquête
La finalité objective en biologie
Interview du professeur Alain Fisher
La sécurité industrielle : prévention des risques majeurs et sécurité au poste de travail
L’industrie pétrolière confrontée au défi de la mobilité durable
Épidémiologie environnementale