Quelles statistiques sont utiles aux entreprises ?

Une entreprise combine trois fonctions essentielles : inventer, fabriquer et vendre. L’exemple de l’industrie pharmaceutique illustre parfaitement cette trilogie. Il lui faut en effet, tout d’abord, découvrir de nouvelles molécules répondant aux besoins de santé, ensuite, fabriquer les préparations destinées à les rendre disponibles aux utilisateurs, et enfin, commercialiser ces dernières afin de générer, in fine, un bénéfice d’exploitation. Naturellement, ce dernier est destiné, d’une part à rentabiliser les investissements antérieurs, et d’autre part à financer la recherche de produits nouveaux.
Au cours de ces différentes opérations, il est constamment nécessaire de pouvoir apprécier les effets thérapeutiques des nouveaux produits, et ceci à partir d’un ensemble d’expériences médicales, dont certaines doivent être conduites sur des patients en cours de traitement. Il est facile de comprendre, dans ce dernier cas, que les données d’observation sont presque toujours coûteuses et peu nombreuses. Il importe donc qu’on puisse en extraire toute l’information disponible, plutôt que de prendre des risques sur la santé de malades en multipliant des protocoles inutiles.
Le problème se pose d’ailleurs dans les mêmes termes lorsqu’il est fait appel à des expérimentations animales. Sans entrer dans le débat de justifier ou non leur existence, chacun sera d’accord sur le fait qu’il serait inacceptable de ne pas chercher à exploiter au mieux les données qu’elles fournissent. Or, par leur nature, les observations auxquelles on peut avoir accès par l’expérience sont imprécises, entachées d’erreur, et aléatoires. C’est ainsi qu’il y a peu de traitements qui soient efficaces à 100 % pour traiter des maladies comme le cancer, et qu’on doive justifier l’intérêt d’une nouvelle médication en fonction de taux de survie à douze ou vingt-quatre mois, plutôt que de compter les guérisons, cette notion perdant d’ailleurs toute signification sur le long terme.
Il faut alors raisonner, non pas sur des patients individuels, mais sur des populations. Comme, pour celles-ci, il n’est pas possible de prévoir avec certitude le détail des réactions des individus qui les composent, on cherchera à mesurer l’incidence globale des actes thérapeutiques auxquelles elles sont soumises.
Le rôle de la statistique est ici essentiel. Aussi bien un mauvais choix du critère de validation qu’une mauvaise utilisation des outils mathématiques qu’elle met en œuvre peut aboutir à des décisions désastreuses. On court ainsi le risque de poursuivre le développement d’un produit dangereux et inefficace, ou, inversement, d’arrêter prématurément l’étude d’une molécule potentiellement riche en applications utiles.
Une approche naïve mènerait à croire que la statistique est un monolithe parfait, au sens qu’il y aurait pour chaque type d’expérience un traitement statistique unique qui lui soit parfaitement adapté. Il n’en est malheureusement rien. Le plus souvent, on doit confronter les données d’observation à de vastes catalogues de modèles mathématiques plus ou moins complexes, et entre lesquels il est difficile de justifier a priori des préférences éventuelles.
D’une certaine manière, l’action du statisticien s’apparente alors à celle du médecin au chevet de son patient. Comme tout bon praticien, son devoir est de bien interpréter les symptômes variés portés à sa connaissance. Les choix qu’il adoptera ensuite pourront avoir des conséquences extrêmes allant de la guérison au décès. Avant tout, il lui importe donc de formuler un bon diagnostic.
Toutefois, on ne peut pas se fier totalement à la seule expérience d’un homme de terrain et il est nécessaire de se livrer à toutes les vérifications possibles avant d’accepter ses conclusions. Il s’agit en effet de distinguer l’information réelle qu’apportent les observations de l’information implicite et subjective qui est induite par les choix de modèle de l’expert en charge de problème. Ceci est loin d’être facile comme on pourra le constater plus loin.
De plus, la pratique de la statistique est rendue d’autant plus difficile qu’elle se doit de combiner une solide expérience avec des connaissances théoriques approfondies. On rencontre souvent l’une sans l’autre. Poursuivant la comparaison entre la statistique et la médecine, il est tout autant dangereux de se faire soigner par des rebouteux que par des biologistes qui n’ont pas une expérience réelle des malades.
Quelques exemples
Plutôt que de rester abstrait, je donnerai quelques exemples pour illustrer mon propos. Le premier, issu de l’industrie pétrolière, concerne les bouchons dans les écoulements diphasiques (voir, par exemple, [2]). Imaginons une plate-forme en pleine mer qui pompe dans un pipeline long de dizaines de kilomètres un mélange composé d’huile, d’eau et de gaz. Sous certaines conditions, l’ensemble se sépare en deux composantes, l’une gazeuse, l’autre liquide, et l’écoulement alternera donc des bulles gazeuses et des bouchons liquides, ces derniers étant propulsés dans le conduit comme la balle dans le canon du fusil.
Il est alors d’une grande importance de quantifier la longueur aléatoire de ces bouchons afin d’adapter au mieux l’appareillage de réception. Si ce dernier a une capacité insuffisante, il sera détérioré par l’arrivée intempestive d’un bouchon de trop grande longueur. Inversement, une trop grande capacité du réservoir de réception serait coûteuse à l’excès au point d’obérer le bénéfice d’exploitation de l’ensemble.
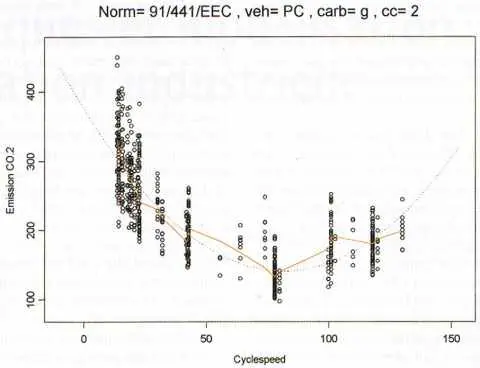
| Comparaison d’une courbe paramétrique et non paramétrique sur un même jeu de données |
|
Mesures d’émission de CO2 (en g/km) pour des véhicules particuliers légers essence de cylindrée comprise entre 1.4 et 2 litres ; en pointillé : courbe théorique ajustée (polynôme du second degré) en trait plein : moyenne mobile. |
Comment procède-t-on pour ajuster les paramètres d’intérêt dans un problème comme celui-ci ? Il est classique de faire usage d’une expérience pilote où l’on ajuste, par des méthodes statistiques standard, une loi de répartition des longueurs de bouchons à partir d’un ensemble limité d’observations. On extrapole ensuite cette loi de répartition pour prévoir les caractéristiques de bouchons extrêmes, ces derniers posant les problèmes de fonctionnement les plus sérieux.
Or, c’est précisément là où le bât blesse : des modèles différents peuvent à la fois s’ajuster fidèlement l’un et l’autre aux données de l’expérience initiale, tout en menant à des prévisions divergentes sur les valeurs extrêmes qu’on doit s’attendre à observer par la suite. Dans cet exemple, le facteur crucial est davantage le bon choix de la loi de répartition des longueurs de bouchons que la façon dont on en ajuste les paramètres à partir de l’expérience. Une erreur dans les choix initiaux du modèle pourra avoir des conséquences catastrophiques.
Mon deuxième exemple vient de l’industrie pharmaceutique. Les efforts qui doivent y être faits, entre l’invention de nouvelles molécules et leur commercialisation, sont extraordinairement longs et coûteux. Il y a peu, la presse a largement fait écho au fait qu’une entreprise prospère pouvait aller à la limite du dépôt de bilan lorsque l’un de ses produits phares était accusé d’effets secondaires inattendus mettant en jeu la santé des consommateurs.
À chaque étape du processus d’évaluation, des expériences délicates doivent être menées pour décider si l’efficacité du produit existe ou non, quantifier ses effets secondaires (et notamment sa toxicité), et décider si l’ensemble de ces caractéristiques justifie qu’on en poursuive le développement jusqu’à son terme. Il suffit parfois d’un mauvais emploi des statistiques pour que l’une de ces analyses mène à abandonner à tort l’étude d’un produit qui aurait généré des bienfaits substantiels, ou inversement à investir à fonds perdus dans des voies improductives.
Il m’a été donné de participer au développement d’une molécule dont les effets remarquables pour le traitement des maladies cardiovasculaires sont maintenant parfaitement connus. Il s’agit du Clopidogrel de Sanofi-Synthélabo. Je me souviens encore d’une expérience menée sur plus de 10 000 patients, et au cours de laquelle l’utilisation d’un modèle statistique inadapté, imposé par un organisme de santé publique étranger, avait failli mener à l’échec.
Le problème était que l’organisme voulait admettre que les taux de mortalité des patients restaient constants au cours de l’expérience (rappelons que le taux de mortalité T(x) d’un patient à l’instant x correspond à une probabilité de décès T(x)dx dans l’intervalle de temps [x,x+dx], sachant que le patient est encore vivant à l’instant x). Il se trouve que le taux de mortalité pour les patients traités avec la nouvelle molécule décroissait avec le temps, ce qui voulait dire que les malades étaient, d’une certaine manière, guéris par ce traitement. Inversement, les patients recevant la médication classique à base d’aspirine conservaient un taux de mortalité constant dans le temps. Ce phénomène, nouveau et inattendu, a été découvert par l’emploi de nouvelles techniques statistiques (voir [3]). S’il n’avait pas été pris en compte à temps, qui sait ce qui aurait pu être déduit d’une étude de cette ampleur analysée sous de mauvaises hypothèses ?
On peut en effet aboutir à des conclusions totalement erronées par l’emploi de modèles inadaptés. Pour bien comprendre le problème, on observera que, pour des taux de mortalité T1 et T2 constants, il n’y a pas d’ambiguïté à préférer le produit (1) au produit (2) si T1 < T2. Le problème est plus complexe lorsque, par exemple, T1(x) dépend du temps x et T2 est constant. En effet, dans ce cas, il peut se faire qu’on observe, pour certaines valeurs des temps x et y, des inégalités telles que T1(x) > T2 et T1(y) < T2. Dans quel cas doit-on alors préférer le produit (1) au produit (2) ? De plus, les méthodes d’estimation adaptées au cas où les T1 et T2 sont constants donnent des résultats sans signification par rapport à la comparaison de T1 et T2 lorsque l’un de ces taux varie avec le temps.
Premières constatations
Au printemps 2001, dans un débat public à l’occasion d’un congrès allemand à Hambourg, j’avais été choqué qu’un intervenant puisse affirmer de bonne foi qu’il ne s’était pas passé grand-chose d’innovant en statistique depuis l’invention du principe du maximum de vraisemblance par Ronald Fisher en 1922. Je m’étais vivement élevé, preuves à l’appui, contre des propos aussi polémiques. Si je me plais à les répéter ici, c’est qu’ils reflètent un point de vue qui voudrait limiter la statistique à l’ajustement des paramètres de modèles (on appelle ceci la statistique paramétrique lorsque le modèle est caractérisé par un nombre fini de paramètres numériques).
En effet, s’il s’agissait seulement d’évaluer un nombre fixé de paramètres réels, décrivant un modèle précis et spécifié, à partir d’observations répétées issues de ce dernier, la méthode du maximum de vraisemblance fournirait certainement des solutions quasiment optimales dans la plupart des cas. Il n’y aurait alors pas besoin d’aller beaucoup plus loin dans l’apprentissage de la statistique.
Or, c’est ignorer la réalité de la statistique que de limiter celle-ci à une situation aussi simple. D’une part, on dispose le plus souvent d’une quantité de modèles candidats pour représenter un même phénomène, et dont le nombre de paramètres peut varier de un à l’infini. D’autre part, il n’est pas non plus réaliste de vouloir choisir entre ces différentes possibilités celle qui convient le mieux par un critère unique, par exemple, en faisant usage de techniques de type Akaike (voir [1]), basées sur la théorie de l’information, et se présentant comme des variantes de la théorie du maximum de vraisemblance, adaptées à un nombre de paramètres variable. Je prendrai un nouvel exemple pour appuyer ce point de vue, sans doute un peu iconoclaste.
Il y a une dizaine d’années, j’avais mis au point un algorithme destiné à améliorer la prévision de séries financières en utilisant une modélisation faisant usage de bruit blanc fractionnaire. J’étais alors à New York, et je fus invité, dans le cadre d’une collaboration industrielle, par une société de services qui s’intéressait à ma méthode.
Quelle ne fut pas ma surprise de voir que cette société utilisait un Cray pour mettre en compétition permanente les unes contre les autres toutes les méthodes connues de prévision de séries temporelles sur un certain nombre de cours de valeurs boursières. Je m’intéressais à un modèle, alors qu’il y en avait des centaines disponibles, au point qu’un utilisateur, même averti, devait utiliser des comparaisons expérimentales pour en faire le tri, et même combiner toutes les prévisions entre elles pour construire une sorte de méta-analyse des cours financiers, en elle-même plus efficace que chacune des méthodes ainsi conjuguées.
Lors d’une analyse statistique isolée d’un ensemble de données, il n’est certes pas possible de procéder, comme ci-dessus, à une validation dynamique de modèles en compétition, à l’instar de celle qui procéderait d’un ajustement sur des séries temporelles observées en temps réel. Toutefois, le statisticien expert se trouve aujourd’hui de plus en plus devant une multitude d’options en concurrence, et entre lesquelles il n’est pas toujours aisé de choisir. Que doit-il faire ? Je suis personnellement convaincu qu’il lui faut explorer systématiquement toutes ces possibilités, plutôt que de se limiter arbitrairement à l’une d’entre elles comme on le voit faire le plus souvent. Certes, ceci demande beaucoup de travail, mais cela présente aussi l’avantage de limiter les risques d’un mauvais choix.
On m’objectera que cette approche risque de créer une confusion certaine, dans la mesure où des modèles différents pourront amener, en toute logique, à des conclusions différentes. La statistique ne serait plus alors un précieux outil d’aide à la décision, mais à l’inverse un facteur de désordre et de contradiction.
J’en viens maintenant aux réponses que je voudrais apporter à la question posée en exergue. La statistique utile aux entreprises est précisément celle qui leur permet de ne pas se tromper, c’est celle qui leur permet de bien choisir entre les possibilités qui leur sont offertes pour l’interprétation des données. D’une part, il convient de ne pas se limiter à un nombre trop restreint de modèles dans les analyses, c’est la conclusion de ce qui précède. D’autre part, il faut faire le bon choix entre les différentes voies possibles, et ceci fera l’objet de notre discussion finale.
Les plus brillantes innovations de la statistique au cours des dernières décennies sont sans conteste dans le domaine des méthodes non paramétriques, où il s’agit d’évaluer la structure des phénomènes avec un minimum d’hypothèses contraignantes. Le vocabulaire de la statistique englobe sous l’appellation de non-paramétrique des modèles qui ne peuvent pas être décrits simplement en fonction d’un nombre fini de paramètres numériques.
À titre d’exemple, dire qu’une variable aléatoire suit une loi de Laplace-Gauss est une hypothèse paramétrique, puisque cette loi est définie par sa moyenne et sa variance. À l’opposé, dire que cette variable a sa loi de probabilité ayant une densité continue est une hypothèse non paramétrique, la loi étant ici définie par une fonction continue positive ou nulle d’intégrale égale à 1. Les outils de la statistique non paramétrique sont, par leur nature même, ceux qui doivent être employés pour valider des modèles plus précis mais en lesquels on n’a qu’une confiance limitée au départ. Nous recommandons donc d’utiliser systématiquement des méthodes non paramétriques en parallèle aux méthodes classiques afin de vérifier si leurs résultats sont en concordance (voir, par exemple, [4]).
Par ailleurs, l’emploi de techniques de rééchantillonnage, telles celles du bootstrap (voir [5]), permettant d’utiliser les données elles-mêmes pour évaluer la précision des estimations en lieu et place des résultats asymptotiques de la théorie classique, devrait entrer dans les mœurs comme une technologie standard.
Sait-on par exemple que l’intervalle de confiance pour la moyenne, basé sur le bootstrap, est bien souvent beaucoup plus précis que l’intervalle de Student habituel ? Un détail comme celui-ci devrait pour le moins éveiller l’attention.
Conclusion
Jusqu’ici, nous nous sommes limités à l’étude des données rares ou précieuses, desquelles il importait de tirer le maximum de renseignements, sans lésiner sur les efforts devant être faits pour parvenir à ce but. Nous avons argué qu’il fallait manipuler la statistique sans trop d’a priori, en essayant, autant que faire se peut, tous les modèles possibles, et en choisissant entre ceux-ci grâce à des analyses non paramétriques menées en parallèle. Il arrive, inversement, que les données soient surabondantes au point qu’il soit difficile d’en dégager une structure quelconque. C’est le problème du » data mining « . Je ne parlerai toutefois pas ici de cette dernière situation, qui mériterait en elle-même une discussion séparée, en mentionnant toutefois que notre analyse s’applique aussi bien à ce cas.
Notre conclusion générale est que les statistiques les plus utiles aux entreprises sont celles qui leur permettent les bons choix de modèles. À partir du moment où un modèle est retenu, le » calage » des paramètres est une opération plus ou moins de routine, grâce, entre autres, à la méthode du maximum de vraisemblance. Toutefois, le risque associé à un mauvais modèle est souvent important, et tout doit être fait pour le réduire. Il faut donc disposer d’outils de validation appropriés, et c’est sur ces derniers que devraient porter les efforts les plus importants.