Réponses à Maurice Allais : Discussion des expériences de Miller

Discussion des expériences de Miller
N° 517 août-septembre 1996

1 — Le principe de l’expérience de Michelson

Une source lumineuse S envoie des rayons sur la lame semi-trans­par­ente L (fig­ure 1).

Une par­tie de ces rayons con­tin­ue vers le miroir M1, revient et est réfléchie vers l’écran E. Une autre par­tie est réfléchie vers le miroir M2, revient et con­tin­ue vers E. Ces deux ensem­bles de rayons inter­fèrent sur l’écran E où l’on con­state effec­tive­ment la présence de franges d’interférences EM1 per­pen­dic­u­laires au plan de la fig­ure 1.

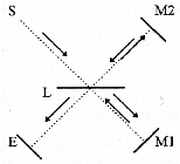Le principe de l’ex­péri­ence de Michelson

Au XIX^e siè­cle on pense que la lumière se propage par les vibra­tions d’un milieu très sub­til et très léger : l’éther qui rem­plit tout l’univers, un peu comme le son se propage par les vibra­tions de l’air, du sol ou de l’eau.

Bien enten­du les corps opaques ont la pro­priété d’éteindre ces vibra­tions et les corps trans­par­ents les lais­sent pass­er, avec une vitesse moin­dre toute­fois et avec un cer­tain entraîne­ment de l’éther mesurés par les expéri­ences de Fres­nel, Fizeau, Fou­cault, Airy.

Dans ces con­di­tions il est naturel de se deman­der qu’elle est la vitesse “ absolue ” de la Terre, c’est-à-dire sa vitesse par rap­port à l’éther.

L’idée de Maxwell et de Michel­son est la suivante :

Si le bras SM1 est ori­en­té dans le sens du mou­ve­ment de la Terre et le bras EM2 dans le sens per­pen­dic­u­laire ce dernier est avan­tagé exacte­ment comme un nageur qui fait un aller retour de 20 m per­pen­dic­u­laire­ment au courant de la riv­ière est avan­tagé par rap­port au nageur qui par­coure la même dis­tance aller retour dans le lit du courant.

En effec­tu­ant alors une rota­tion de 90° de l’ensemble de l’interféromètre on trans­fère l’avantage au bras SM1 et l’on doit donc con­stater un déplace­ment appro­prié des franges d’interférence sur l’écran E. L’ampleur du déplace­ment per­me­t­tra de con­naître la vitesse “ absolue ” de la Terre.

2 — Les expériences

La pre­mière expéri­ence d’Albert Michel­son en 1881 n’est pas con­clu­ante aus­si recom­mence-t- il en 1887 avec l’aide d’Edward Mor­ley mais le déplace­ment des franges obtenu n’est pas le dix­ième de celui qui cor­re­spondrait au 30 km/s de la vitesse orbitale de la Terre ; c’est décourageant.

Ce résul­tat négatif va inciter indépen­dam­ment Lorentz et Fitzger­ald à pro­pos­er la “ con­trac­tion de Lorentz-Fitzger­ald ” : le vent d’éther provoque une con­trac­tion lon­gi­tu­di­nale des objets dans le rap­port qui con­vient soit :

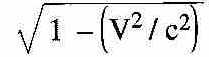où V est la vitesse de l’objet étudié et c celle de la lumière.

Cette con­trac­tion bien sur­prenante et faite pour les besoins de la cause a un côté “ coup de pouce ” qui déplaît à Hen­ri Poin­caré. La cor­re­spon­dance qu’il échange avec Lorentz sur ce sujet pen­dant près de dix ans le con­duit à :

A) Renon­cer au temps absolu, à l’espace absolu, à l’éther (La Sci­ence et l’Hypothèse, 1902).

B) Énon­cer le “ Principe de Relativité ”.

Les lois des phénomènes physiques doivent être les mêmes pour un obser­va­teur fixe et pour un obser­va­teur entraîné dans un mou­ve­ment rec­tiligne et uni­forme de sorte que nous n’avons et ne pou­vons avoir aucun moyen de dis­cern­er si nous sommes oui ou non entraînés dans un pareil mou­ve­ment.

Au con­grès sci­en­tifique mon­di­al de Saint-Louis (Mis­souri, sep­tem­bre 1904) Hen­ri Poin­caré con­sacre la majeure par­tie de sa con­férence véri­ta­ble­ment his­torique à la présen­ta­tion et à la défense de ce principe.

C) Quelques mois plus tard Poin­caré établit que le Principe de Rel­a­tiv­ité con­duit à la trans­for­ma­tion de coor­don­nées qu’il bap­tise “ Trans­for­ma­tion de Lorentz ”, laque­lle a la pro­priété de con­serv­er les équa­tions de Maxwell et explique très sim­ple­ment la con­trac­tion de Lorentz-Fitzger­ald : c’est un effet de per­spec­tive lié à une “ rota­tion dans l’espace-temps ”, c’est-à-dire à la mise en route d’un objet, et tout à fait ana­logue aux effets de per­spec­tive que l’on con­state pour les rota­tions ordi­naires dans l’espace.

Les fonde­ments de la Rel­a­tiv­ité sont ain­si établis.*

Il con­vient cepen­dant de véri­fi­er avec plus de pré­ci­sion les résul­tats de Michel­son et Mor­ley et d’en tir­er tout le par­ti pos­si­ble. Au con­grès de physique de Paris (1900) Lord Kelvin lance un appel pres­sant dans ce sens, appel qu’Edward Mor­ley et son col­lab­o­ra­teur Day­ton Miller déci­dent de relever.

De 1902 à 1906 Mor­ley et Miller, puis de 1921 à 1926 Miller seul, iront de per­fec­tion­nements en per­fec­tion­nements. Ils allongeront les bras de leur inter­féromètre et mul­ti­pli­eront les aller retour pour aug­menter la sen­si­bil­ité. Ils passeront d’une struc­ture de bois et de grès, à l’acier et au béton, le tout flot­tant sur un bain de mer­cure pour obtenir une rota­tion impec­ca­ble. Ils sur­veilleront l’influence de la tem­péra­ture, de la pres­sion, du champ mag­né­tique ter­restre, du vent. Ils recom­menceront l’expérience en divers lieux (Cleve­land, mont Wil­son), à divers­es heures et saisons. Ils accu­muleront plusieurs cen­taines de mil­liers de mesures selon un pro­to­cole très strict.

En défini­tive Miller pour­ra proclamer que, même s’il n’obtient pas le mou­ve­ment absolu de la Terre, il obtient tout de même des résul­tats intéres­sants en désac­cord avec la théorie de la Relativité.

Pen­dant ce temps d’autres expéri­men­ta­teurs procè­dent à la même expéri­ence sans toute­fois mul­ti­pli­er autant les mesures : Roy Kennedy puis Illing­worth à Pasade­na ; Auguste Pic­card et E. Sta­hel à Brux­elles puis en Suisse ; Albert Michel­son, F. G. Paese et F. Pear­son au mont Wil­son ; Georg Joos à Iéna.

Tous obti­en­nent des résul­tats “ négat­ifs ” : pas de déplace­ment des franges à la pré­ci­sion des mesures…

3 — Discussion

Com­ment ces deux séries de résul­tats peu­vent-elles être aus­si dif­férentes ? Miller peut met­tre en avant le nom­bre énorme de ses mesures et la var­iété de ses con­di­tions expéri­men­tales, ses col­lègues ont pour eux leur una­nim­ité et l’unicité de leurs résul­tats. Il y a cepen­dant une dif­férence essen­tielle entre ces expéri­ences : Miller opère à l’air libre, il pré­conise de “ laiss­er cir­culer l’éther autant que faire se peut ” et utilise au max­i­mum le verre quand il est for­cé de met­tre une paroi. Ses col­lègues au con­traire enfer­ment leurs inter­féromètres dans des récip­i­ents solides et bien fer­més, la plu­part du temps ils y font le vide pour dimin­uer le plus pos­si­ble les sources extérieures de perturbation.

C’est sans doute là l’explication. Il con­vient de se rap­pel­er que la “ con­trac­tion de Lorentz- Fitzger­ald ” est extrême­ment faible : avec V/ c = 0,0001 cette con­trac­tion n’est que de cinq mil­liardièmes et l’effet obtenu par Miller est sept ou huit fois plus petit…

L’indice optique de l’air est certes voisin de 1 mais il n’est pas 1, il vaut 1,000294 à 0° et 1 013 mil­libars et sa dif­férence à 1 est à peu près pro­por­tion­nelle à la den­sité de l’air.

Il suf­fit d’une vari­a­tion d’un mil­lième de degré pour obtenir les résul­tats de Miller… Qui sait ? peut-être tout sim­ple­ment ces résul­tats indiquent-ils que les coins Nord et Sud de son lab­o­ra­toire avaient une tem­péra­ture moyenne un mil­lième de degré plus faible, env­i­ron, que les coins Est et Ouest… et il n’y aurait rien de sur­prenant à ce que cette dif­férence évolue péri­odique­ment avec les heures et les saisons comme l’indiquent les résul­tats. Mais il con­vient aus­si d’admirer le sérieux et la remar­quable minu­tie de Miller !

De toute façon l’expérience de Michel­son n’est pas le fonde­ment de la Rel­a­tiv­ité, c’est tout au plus “ la goutte d’eau qui a fait débor­der le vase ”. Ce qui se passe dans un cyclotron est bien plus sig­ni­fi­catif : pour faire tourn­er à la vitesse V une par­tic­ule de charge q et de “ masse au repos” m0 sur un cer­cle de ray­on R il faut une induc­tion mag­né­tique B nor­male au plan du cer­cle et don­née par une expres­sion typ­ique­ment relativiste :

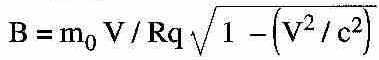
Le rap­port V / c n’est ici pas lim­ité à 0,0001, il peut aller aisé­ment à 0,99 et même davantage.

4 — Conclusion

Les expéri­ences de Day­ton Miller ne sem­blent pas aus­si sig­nifi­antes que l’on aurait pu l’espérer ou le crain­dre, mais il faut tout de même remerci­er Mon­sieur Mau­rice Allais d’avoir attiré notre atten­tion sur ces expéri­ences “ hérétiques ”.

Nous n’avons que trop ten­dance à pass­er sous silence ce qui n’est pas en accord avec nos idées (et per­son­nelle­ment je n’avais jamais enten­du par­ler de Day­ton Miller). C’est là un réflexe par­faite­ment anti-sci­en­tifique et stu­pide car il y a sou­vent beau­coup plus à appren­dre d’une expéri­ence rigoureuse­ment con­duite et qui ne marche pas que d’une expéri­ence qui marche.

Dans cet ordre d’idées, il faut soulign­er que par­mi les trois tests clas­siques de la Rel­a­tiv­ité générale (avance du péri­hélie de Mer­cure, cour­bu­re des rayons lumineux au voisi­nage du Soleil et effet Ein­stein de décalage vers le rouge des raies spec­trales émis­es à la sur­face des étoiles) on par­le beau­coup des deux pre­miers et assez peu du troisième. Cela s’explique : cet effet marche assez mal. Il est bien véri­fié si votre obser­va­tion porte sur les bor­ds du disque solaire mais est deux à trois fois trop petit dans les régions cen­trales (réf. 2).

Peut-être y a‑t-il là matière à réflexion.

* Hen­ri Poin­caré ne sur­vivra guère à ce tra­vail de géant ; fort heureuse­ment ses travaux seront repris et pop­u­lar­isés par Her­mann Minkowsky et Albert Ein­stein. Ce dernier présen­tera la Rel­a­tiv­ité si magis­trale­ment que beau­coup s’imaginent qu’il en est l’auteur, alors que ses auteurs véri­ta­bles sont Hen­drik Antoon Lorentz et surtout Hen­ri Poincaré.

5 — Références

1) Day­ton C. Miller, The Ether – Drift Exper­i­ment and the Deter­mi­na­tion of the Absolute Motion of Earth, Review of Mod­ern Physics, Vol. 5, p 203–242, July 1933.

2) S. Mavridès, L’Univers rel­a­tiviste, p. 122–123, Mas­son et Cie édi­teurs, Paris, 1973.

Christian MARCHAL (58)

Expérience de Miller et validité de la relativité restreinte

Résumé

Par une série d’expériences effec­tuée dans les années 20, sim­i­laires à celle de Michel­son-Mor­ley, Day­ton Miller a affir­mé avoir mis en évi­dence un mou­ve­ment de la Terre par rap­port à l’éther, c’est-àdire l’espace absolu de New­ton. Dans le numéro de sep­tem­bre 1996 de La Jaune et la Rouge, Mau­rice Allais analyse à nou­veau les résul­tats de ces expéri­ences et con­clut qu’ils réfu­tent la rel­a­tiv­ité restreinte. Nous mon­trons qu’il n’en est rien en faisant un bref his­torique des expéri­ences de ce type, résumant ce qu’elles ont effec­tive­ment mesuré et pour­raient encore éventuelle­ment montrer.

La cinématique de Newton est caduque

On sait depuis le XIX^e siè­cle que les équa­tions de Maxwell de l’électromagnétisme n’ont pas la même forme dans deux repères iner­tiels dif­férents si le pas­sage de l’un à l’autre est régi par la loi de trans­for­ma­tion de Galilée. On sait aus­si que les physi­ciens de l’époque cher­chèrent à met­tre à prof­it cette pro­priété pour mesur­er la vitesse absolue de la Terre, c’est-à-dire sa vitesse de trans­la­tion par rap­port à “ l’éther ”, le milieu absol­u­ment au repos pos­tulé par New­ton dans lequel les objets obéis­sent à ses lois du mou­ve­ment et par rap­port auquel les repères iner­tiels sont en trans­la­tion uniforme.

Les expéri­ences furent menées à l’aide d’interféromètres qui, selon la théorie, devaient mesur­er (v_abs/c)² où v_abs est la vitesse absolue de la Terre et c celle de la lumière. Cette vitesse absolue peut se décom­pos­er (en igno­rant pour sim­pli­fi­er les effets d’orientation) en v_abs = v_cos + v_orb + v_rot où v_rot ≈ 0.4 km/s est la vitesse d’un lab­o­ra­toire à l’équateur due à la rota­tion de la Terre sur elle-même, v_orb ≈ 30 km/s la vitesse orbitale de la Terre autour du Soleil et v_cos une éventuelle vitesse “ cos­mique ” du sys­tème solaire par rap­port aux étoiles loin­taines sup­posées au repos dans le repère absolu. On s’attendait donc à mesur­er au moins v_orb c’est-à-dire un effet de l’ordre de (v_orb/c)² ≈ 10^-8. Et si l’on prend pour v_cos la vitesse du sys­tème solaire par rap­port au ray­on­nement cos­mique de fond à 3 degrés Kelvin, c’est-à-dire ≈ 300 km/s, l’effet atten­du devient de l’ordre de 10^-6.

Les expéri­ences furent nom­breuses : Michel­son 1881, Michel­son et Mor­ley 1887, Mor­ley et Miller 1902–1906, Miller 1921, 1924–1926, Kennedy 1925, Picard et Sta­hel 1926, Michel­son 1929, Joos 1930, Kennedy et Thorndike 1932, Ives et Stil­well 1938 et 1941, Townes et al. 1958 et 1964 et enfin Bril­let et Hall 1979 (Phys. Rev. Let­ters 42 (1979) 549).

Aucune de ces expéri­ences ne mesura un effet de l’amplitude escomp­tée. Ceci étant, aucune, bien sûr, ne mesura un effet stricte­ment nul… Le prob­lème, comme tou­jours en physique expéri­men­tale, est en d’interpréter les effets résidu­els, de déter­min­er s’ils sont sig­ni­fi­cat­ifs ou imputa­bles à des erreurs expéri­men­tales. Mais tous les expéri­men­ta­teurs, à l’exception de Day­ton Miller, estimèrent que leurs résul­tats étaient dans les bar­res d’erreurs de leur expéri­ence et donc com­pat­i­bles avec zéro. Quant à la pré­ci­sion elle crût avec les développe­ments tech­nologiques du siè­cle : Michel­son, en 1881, trou­va que l’effet devait être inférieur à 10^-9, Bril­let et Hall, en 1979, trou­vèrent que l’effet, s’il était d’origine locale, devait être inférieur à 10^-13 et inférieur à 10^-15 s’il était d’origine cos­mique. Pour inter­préter ces résul­tats bien inférieurs à ceux aux­quels on s’attend dans le cadre de la théorie clas­sique et tous com­pat­i­bles avec zéro, sauf celui de Miller, on peut bien sûr invo­quer, comme le fit Lorentz, des phénomènes de con­trac­tion de longueur ou d’entraînement de l’éther. Mais on sait que la solu­tion pro­posée par Ein­stein l’emporta et ces expéri­ences scel­lèrent le tri­om­phe de sa théorie de la rel­a­tiv­ité restreinte.

Les conclusions de Miller doivent être rejetées

Day­ton Miller était d’après ses con­tem­po­rains un expéri­men­ta­teur de haut vol qui col­lab­o­ra avec Michel­son avant de lui suc­céder à la chaire de physique de l’université de Cleve­land. Son arti­cle de revue de 1993 (Rev. of Mod. Phys. vol. 5 p. 203) sur lequel Mau­rice Allais base son analyse est un mod­èle de clarté et de rigueur. De plus Miller a été le seul à répéter ses expéri­ences à dif­férents moments de l’année, dans le but d’obtenir non seule­ment l’amplitude mais aus­si la direc­tion de la vitesse absolue de la Terre.

Ses résul­tats dif­fèrent de tous les autres : comme Michel­son et Mor­ley il trou­ve un effet résidu­el de l’ordre de 10^-9 cor­re­spon­dant à une vitesse absolue v_abs ≈ 10 km/s, mais con­traire­ment à eux, il estime qu’il est sig­ni­fi­catif. En analysant ses don­nées il peut même décom­pos­er v_abs en v_abs = v_cos + v_orb où v_cos pointe dans la direc­tion du pôle sud de l’écliptique et où v_orb»1.5 km/s.

Ses résul­tats sont cepen­dant dif­fi­ciles à inter­préter, même dans le cadre de la théorie clas­sique, et ce pour deux raisons, ain­si qu’il le souligne lui-même. Comme la vitesse orbitale de la Terre est con­nue et vaut 30 km/s et qu’il ne mesure que 1.5 km/s, il est obligé d’invoquer un fac­teur d’entraînement de l’éther d’environ de 1.5/30, à expli­quer. Par ailleurs la direc­tion de v_cos devrait tra­vers­er la ligne Nord-Sud chaque jour à cause de la rota­tion de la Terre sur elle-même. Or, notr Miller, si v_cos tra­verse bien un axe deux fois par jour, cet axe est déplacé par rap­port au méri­di­en, de façon var­iée suiv­ant la péri­ode de l’année. C’est en fait cette anom­alie azimu­tale, plus que le fac­teur d’entraînement de l’éther, qui sem­ble avoir été la rai­son du doute jeté dès les années 20 sur ses résultats.

En 1995 cepen­dant, des chercheurs de Cleve­land, Shank­land et al. (Review of Mod­ern Physics, vol. 27, p. 167) analysèrent à nou­veau les don­nées de Miller, à par­tir de son arti­cle de 1933 mais aus­si de ses cahiers d’expérience. Ils con­fir­mèrent que l’amplitude de l’effet mesuré n’était pas un effet du hasard sta­tis­tique. Mais les anom­alies azimu­tales les incitèrent à chercher une cause locale plutôt que cos­mique à l’effet mesuré. Ils étudièrent donc, plus atten­tive­ment que ne l’avait fait Miller lui-même, les erreurs sys­té­ma­tiques qui auraient pu en être la cause. Ils en trou­vèrent une : un gra­di­ent de tem­péra­ture de 0,001 degré d’un bout à l’autre du lab­o­ra­toire suff­i­sait à pro­duire un effet de 10^-9. Or Miller, con­traire­ment à ses con­tem­po­rains comme par exem­ple Joos, pou­vait dif­fi­cile­ment réguler la tem­péra­ture de son lab­o­ra­toire : afin en effet de per­me­t­tre à l’éther de cir­culer libre­ment et ne pas être entraîné avec l’interféromètre, il opérait dans une hutte au som­met du mont Wil­son, mal isolée ther­mique­ment. (Il est intéres­sant de remar­quer que les tests qu’il effec­tua dans son lab­o­ra­toire de Cleve­land où la tem­péra­ture était remar­quable­ment con­stante don­naient un effet com­pat­i­ble avec zéro…).

Il sem­ble donc clair que les résul­tats de Miller con­cer­nant l’amplitude de l’effet, c’est-à-dire le mod­ule de la vitesse absolue de la Terre, ne peu­vent plus être retenus, encore moins ceux con­cer­nant la direc­tion de cette vitesse.

Que prédit la relativité ?

On présente tou­jours les résul­tats com­pat­i­bles avec zéro des expéri­ences de type Michel­son- Mor­ley comme une con­fir­ma­tion écla­tante de la rel­a­tiv­ité restreinte. Je voudrais con­clure en com­men­tant ce point.

On sait qu’Einstein, con­fron­té à la non-invari­ance des équa­tions de Maxwell dans les trans­for­ma­tions de Galilée, déci­da, con­traire­ment aux “ clas­siques ”, de pari­er pour le principe de rel­a­tiv­ité : toutes les lois de la physique doivent avoir la même forme dans tout repère iner­tiel afin qu’aucun phénomène ne puisse met­tre en évi­dence le mou­ve­ment de ce repère par rap­port à un autre repère iner­tiel. Pour que les équa­tions de Maxwell gar­dent la même forme il fal­lait donc chang­er la loi de trans­for­ma­tion, plus pré­cisé­ment rem­plac­er celle de Galilée par celle de Lorentz. Cette théorie de la rel­a­tiv­ité restreinte était une vision révo­lu­tion­naire car elle impli­quait une mod­i­fi­ca­tion pro­fonde des représen­ta­tions de l’espace et du temps ancrées depuis New­ton. On se doute qu’un tel change­ment ne fut pas accep­té sans de solides débats et de solides con­fir­ma­tions expérimentales.

Ain­si la loi de trans­for­ma­tion de Lorentz qui régit le pas­sage d’un repère iner­tiel à un autre est main­tenant véri­fiée à 10-²², de la façon suiv­ante : si elle n’était pas valide, les lois de Maxwell seraient dif­férentes et la sépa­ra­tion des niveaux du noy­au de lithi­um dans un champ mag­né­tique (effet Zee­man) serait dif­férente de ce que donne la for­mule “ stan­dard ” et con­fir­mée par l’expérience (Hugh­es-Drev­er, 1961). (Pour une revue détail­lée des tests de la rel­a­tiv­ité voir Clif­ford M. Will The­o­ry and exper­i­ment in grav­i­ta­tion­al physics, Cam­bridge Uni­ver­si­ty press, 1993.)

Cette extra­or­di­naire con­cor­dance entre théorie et expéri­ence sig­ni­fie- t‑elle qu’une expéri­ence de type Michel­son-Mor­ley effec­tuée avec une gran­dis­sante pré­ci­sion don­nerait tou­jours un résul­tat com­pat­i­ble avec zéro ?

Ce que dit la rel­a­tiv­ité restreinte est que la vitesse de la lumière doit être la même dans tous les repères iner­tiels. La ques­tion devient donc de savoir si un inter­féromètre attaché à la Terre est un repère iner­tiel. La réponse, bien sûr, est non : un lab­o­ra­toire sur Terre n’est pas stricte­ment en mou­ve­ment libre. Il est d’abord soumis au champ de grav­i­ta­tion de la Terre, qui induit des forces de marées sur l’appareil. On mon­tre cepen­dant que ces forces, pro­por­tion­nelles à la dimen­sion de l’appareil mul­ti­pliée par la racine car­rée de la cour­bu­re locale de l’espace-temps, sont tout à fait nég­lige­ables. Beau­coup plus impor­tantes en revanche peu­vent être a pri­ori les forces d’inertie dues au fait que le lab­o­ra­toire tourne, entraîné par le mou­ve­ment diurne de la Terre. Pour cal­culer ces forces, il faut savoir pass­er d’un repère iner­tiel à un repère tour­nant en rel­a­tiv­ité restreinte, et décrire dans ce repère un appareil “rigide”.

Ce sont là choses non triv­iales, encore vive­ment débattues. Si l’effet existe il serait en tout cas de l’ordre de (v_rot/c)², soit de » 10^-13. Une expéri­ence amélio­rant d’un ordre de grandeur ou deux la pré­ci­sion de celle de Bril­let et Hall devrait pou­voir infirmer ou con­firmer cette pré­dic­tion (cf. L. Bel, J. Mar­tin et A. Moli­na, Jour­nal of the Phys. Soc. of Japan, vol. 63 (1994) 4350).

Si l’expérience de Michel­son- Mor­ley doit être à nou­veau dis­cutée, c’est donc je pense dans cette ligne là qu’elle doit l’être, et non en ter­mes d’une ciné­ma­tique new­toni­enne main­tenant dépassée.

Nathalie DERUELLE,
maître de conférences à l’École polytechnique,
Département d’astrophysique relativiste et de cosmologie,
Centre national de la recherche scientifique, Observatoire de Paris

---

Articles similaires :

À pro­pos de l’article “Pour qui roulent les poly­tech­ni­ciens ?” de Marc Flen­der (92), n° 585, mai 2003 AU COURRIER : Deux réflex­ions sur l’énergie Arti­cles sur Descartes des numéros de novem­bre et décem­bre 1996 Divers : La local­i­sa­tion d’Alésia (N°520) et L’espace-temps de J.-P. Auf­fray (N°522) Le cour­ri­er des lecteurs : trois interventions Cour­ri­er des lecteurs