SARS-CoV‑2 : « Où est caché le loup ? »

« L’obsession de précision numérique sans attention aucune à la pertinence est le meilleur traceur de l’absence de culture mathématique véritable. »
Carl Friedrich Gauss (1777–1855)

Début mars 2020, je pré­parais une nav­i­ga­tion de Roscoff à Ham­mamet en voili­er sans penser que ce périple allait être mis à mal par un phénomène en train de devenir mon­di­al à cause d’une « besti­ole » au nom presque imprononçable : le SARS-CoV­‑2. Frus­tré par cette atteinte à ma lib­erté chérie, je me suis rabat­tu sur une nav­i­ga­tion intel­lectuelle dans des con­trées que je ne fréquente pas habituelle­ment, et j’ai cher­ché à me faire une opin­ion d’honnête homme sur le phénomène en ques­tion et sa « besti­ole ». C’est ce périple que je vous pro­pose d’accom­plir en ma compagnie.

Petite navigation d’essai en Virussie

À peine par­tis et déjà un pre­mier débat se fait jour : cette « besti­ole » n’en est pas une, et pourtant…

Un virus n’est sans doute pas un organ­isme vivant : c’est un triste sire qui ne se repro­duit pas, ni en soli­taire, ni avec des ami(e)s ; il se réplique par con­tre, plutôt comme un par­a­site, en détour­nant à son prof­it la machiner­ie géné­tique de nos petites cel­lules à nous. Alors, un virus est un être ou un non-être ? Shake­speariens en dia­ble, ces virus.

Je passerai sur les don­nées con­nues de ce virus, virus à ARN Classe IV, intro­duc­tion dans nos cel­lules via sa pro­téine Spike et le récep­teur ACE2 de nos cel­lules, ciblage prin­ci­pale­ment des cel­lules épithéliales de notre appareil res­pi­ra­toire, mais pas que… etc. Je cit­erai cepen­dant une spé­ci­ficité de ce virus : il con­tourne une défense immu­ni­taire (inhi­bi­tion de la sécré­tion d’interféron) ET « en même temps » (oui, je sais…) il ren­force « l’appel aux armes » généré par les cytokines qui créent une accu­mu­la­tion de neu­trophiles et macrophages dans nos organ­ismes, cet excès générant des lésions sou­vent fatales.

Avec quelles cartes et quelles données va-t-on naviguer ?

Encore des débats ouverts… Les cas infec­tés dépen­dent de la poli­tique de tests, les tests ne sont pas super fiables, ils ne tes­tent pas tous la même chose, et puis on ne peut pas tester tout le monde, et puis il y a les asymp­to­ma­tiques, et puis les décès ne sont pas tous compt­abil­isés, et puis les caus­es des décès sont mul­ti­ples et pas toutes attribuables au seul virus… etc.

Pour notre nav­i­ga­tion, nous utilis­erons les seules don­nées réper­toriées « décès par 24h à l’hôpital » col­lec­tées par San­té Publique France [1]. Ce sont les don­nées les moins sujettes à cau­tion dont nous dis­posons et elles représen­tent une sous-pop­u­la­tion de la pop­u­la­tion française impor­tante en nom­bre et en tout cas très sig­ni­fica­tive. Les don­nées sur les cas recen­sés (tests posi­tifs) sont à éviter car dif­fi­cile­ment inter­préta­bles en dehors d’étude spé­ci­fique sur échan­til­lon suff­isam­ment grand et représentatif.

Nous avons représen­té les don­nées disponibles jusqu’au 21 août 2020.

Dans tout le reste du doc­u­ment quand nous par­lerons des décès, ce sera tou­jours de ces décès-là dont nous parlerons.

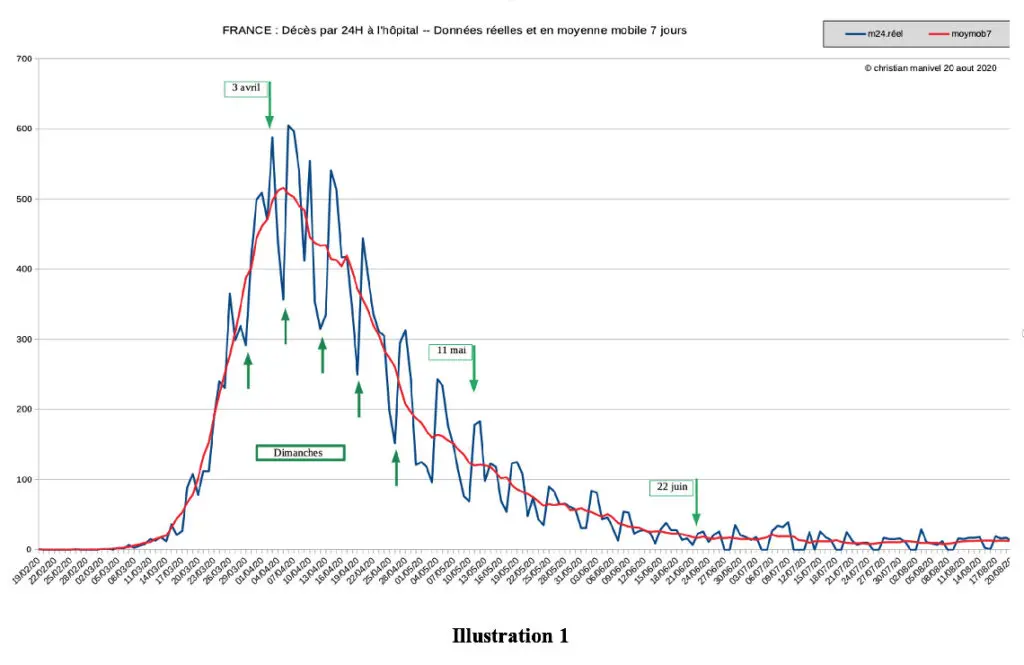
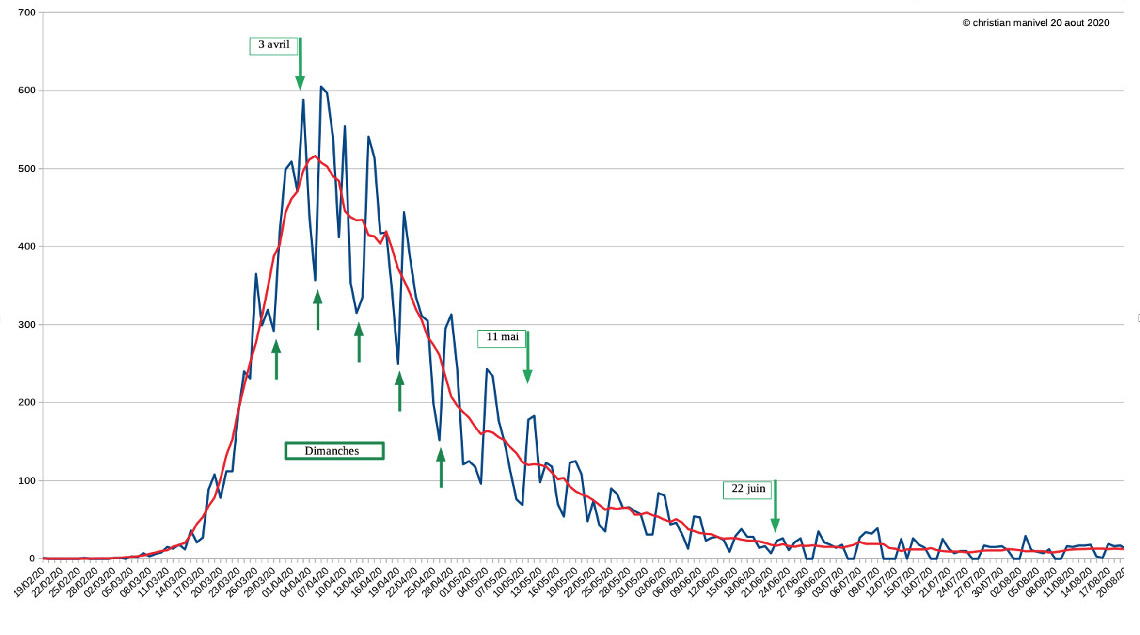
L’illustration 1 ci-dessous décrit ces don­nées à par­tir du 19 févri­er 2020.

Au pre­mier regard, on voit un phénomène de saison­nal­ité heb­do­madaire, qui con­siste en une sous-col­lecte des don­nées le week-end, com­pen­sée par une sur-déc­la­ra­tion le lun­di et par­fois le mar­di suivants.

Avec mon mau­vais esprit habituel j’ai tout de suite pen­sé à une nou­velle « excep­tion française ». Eh bien non, à l’examen des don­nées mon­di­ales et pays par pays (mer­ci Johns Hop­kins Uni­ver­si­ty) cette excep­tion est en fait mon­di­ale. (Pour ceux qui sont encore atten­tifs, oui il y a bien un « s » à Johns).

Les moyennes mobiles à sept jours sont donc égale­ment représen­tées pour gom­mer le phénomène des week-ends, mais nous avons tra­vail­lé ultérieure­ment avec les deux types de don­nées (brutes ou MM7jours)

Au deux­ième regard, on peut observ­er que, depuis le 11 juil­let, le nom­bre des décès quo­ti­di­ens varie entre 9 et 13 (en moyenne mobile 7 jours). On ne manque pas d’être sur­pris, dès lors, par nom­bre de com­men­ta­teurs qui aler­tent, alar­ment et cri­ent au loup sur les per­spec­tives de la ren­trée de sep­tem­bre, au vu des chiffres quo­ti­di­ens des cas d’infection con­statés en juil­let et en août. Ils ont l’air d’oublier que les décès d’aujourd’hui suiv­ent pro­por­tion­nelle­ment les mêmes courbes que les infec­tions d’hier (certes décalés de 15 jours env­i­ron). Imag­inez un nav­i­ga­teur qui déclare prévoir le prochain coup de vent en analysant les vari­a­tions du clapot alors qu’il nav­igue par force 1 !

Je vous invite à regarder les don­nées réelles depuis même la date du décon­fine­ment défini­tif du 22 juin : si ça n’est pas du clapot, ça y ressem­ble grandement.

Une escale technique dans la cité modèle de Kermack et McKendrick 

Le pro­pre d’une escale tech­nique, ce n’est pas la détente : point de pub, point de musique irlandaise, point de tapa­le­rias non plus, … on fait seule­ment le plein de ressources qui nous seront utiles pour la nav­i­ga­tion future.

L’architecture de la cité 

Après Ross & Hud­son en 1917, nos amis Ker­ma­ck & McK­endrick [2] ont con­stru­it vers 1927 une nou­velle cité dont l’architecture est la suivante :

• une seule infec­tion peut engen­dr­er un proces­sus autonome de développe­ment de l’infection ;
• le résul­tat de la mal­adie est l’immunité ou le décès ;
• les con­tacts suiv­ent la loi d’action de masse (le nom­bre de con­tact entre sus­cep­ti­bles et infec­tés par unité de temps et de sur­face est pro­por­tion­nel au pro­duit de leurs den­sités spa­tiales respectives) ;
• tous les indi­vidus sont sus­cep­ti­bles de manière indif­féren­ciée (homogénéité) ;
• la pop­u­la­tion est fer­mée (effet démo­graphique nég­lige­able sur la péri­ode con­cernée par l’épidémie) ;
• la pop­u­la­tion est suff­isam­ment grande pour garan­tir la per­ti­nence d’un mod­èle déter­min­iste (vs. stochastique).

Les équations qui en résultent

La manière dont les hypothès­es ci-dessus con­duisent aux équa­tions du mod­èle est par­ti­c­ulière­ment intéres­sante et je vous con­seille vive­ment la lec­ture du jour­nal de bord cité en référence [4] dans lequel elles sont consignées.

Nous n’en rap­pellerons que les élé­ments clés :

R° est sou­vent appelé nom­bre de repro­duc­tion basique, il est fon­da­men­tale­ment asso­cié au temps t=0, au démar­rage de l’épidémie. Par­ler de R° au cours de l’épidémie est symp­to­ma­tique d’une mau­vaise con­nais­sance du sujet …

R° = β.Ti.S°

Lorsque R° est > 1, le sys­tème con­verge vers un état d’équilibre sta­ble (S∞ ; 0) et une épidémie a lieu ; lorsque R° est < 1 les infec­tions décrois­sent immé­di­ate­ment à par­tir de I°.

Ti = 1/γ est la durée moyenne de l’infection.

β est le coef­fi­cient d’infectivité.

S(t) est la pop­u­la­tion des indi­vidus sus­cep­ti­bles d’être infec­tés, I(t) celle des infec­tés au sens du mod­èle [6].

S° et I° les con­di­tions ini­tiales à t =0 et Im la valeur max­i­male de I.

La langue parlée dans le pays des modèles

Nous allons main­tenant pour­suiv­re notre nav­i­ga­tion au pays des mod­èles, en gar­dant à chaque étape comme but de rap­procher, sur de plus en plus longues péri­odes, les mod­èles des seules don­nées que nous avons con­sid­érées comme per­ti­nentes, à savoir les chiffres des décès par 24h.

Je ne vous l’ai pas dit, mais ce pays des mod­èles est peu­plé de tribus divers­es, les Logues, très accueil­lants d’ailleurs, les Logistes, etc., mais la tribu prépondérante est la tribu des Zateurs. Inutile de vous dire qu’ils ont tous des langues dif­férentes, dont cer­taines sont par­fois intraduisibles.

Très peu de Iciens par con­tre, avec lesquels nous auri­ons pour­tant eu une affinité par­ti­c­ulière, c’est dom­mage car nous auri­ons com­pris plus aisé­ment leur langue.

Quant aux Zateurs, ils adorent un dieu par­ti­c­uli­er qu’ils appel­lent R° (je con­nais­sais Ra et Rê mais bon, pourquoi pas R° ?). Comme beau­coup de dieux, il est mul­ti­formes : il représente un cer­tain com­porte­ment à l’origine et « en même temps » (décidé­ment, on dirait que les sys­tèmes sim­ples sont en noir et blanc et les sys­tèmes com­plex­es ou vivants sont « en même temps ») il est fon­da­men­tale­ment lié à l’équilibre du sys­tème (à l’infini) et surtout à la sta­bil­ité de cet équili­bre… Il y a même des livres entiers sur ce dieu R° [3].

Il nous faut donc nous famil­iaris­er avec la langue des Zateurs et pour ce faire nous promen­er dans la représen­ta­tion des modèles.

Nou­velle ques­tion exis­ten­tielle : c’est quoi un modèle ?

Pour faire sim­ple et utile pour notre nav­i­ga­tion future, nous dirons que c’est un ensem­ble d’EDO muni de con­di­tions ini­tiales et de paramètres adéquats (oui, je sais, beau­coup de choses sont dans le « adéquats », sen­si­bil­ité, iden­ti­fi­a­bil­ité, etc. mais cela n’est pas l’objet de notre périple). Tous les mod­èles des Zateurs, même les plus sophis­tiqués, suiv­ent ces principes. On utilis­era sou­vent le terme mod­èle SIR pour les désigner.

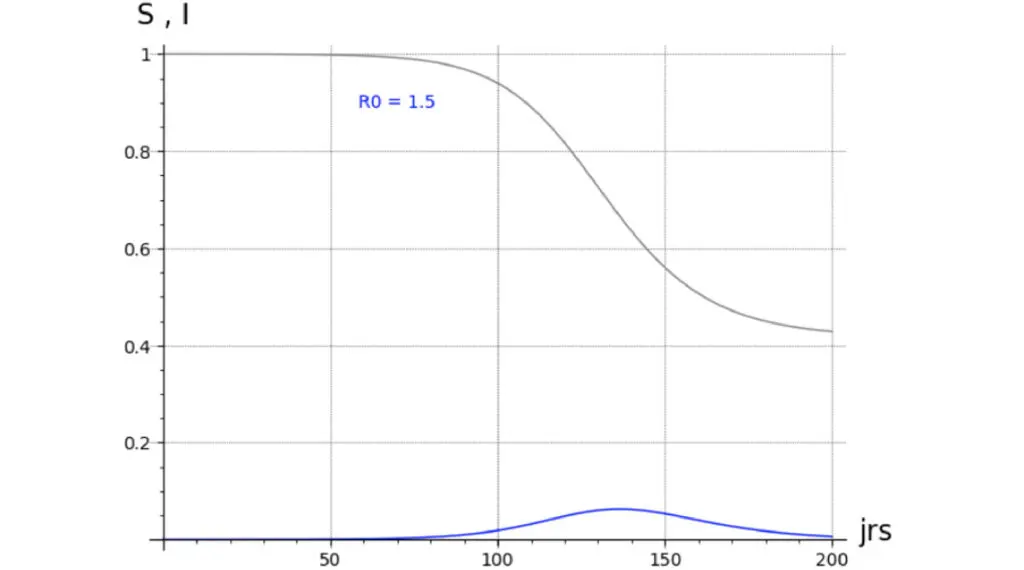
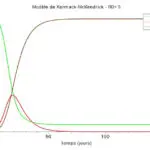
Un bon dessin valant mieux qu’un long dis­cours, les illus­tra­tions 2.1 à 2.4 suiv­antes, représen­tant une épidémie fic­tive, mon­trent l’allure de dif­férents modèles :

Représen­ta­tion de S(t) et I(t)) pour :

- des R° (>1) dif­férents (10.0, 3.0, 2.0, 1.5) (c’est à dire pour des infec­tiv­ités β différentes),

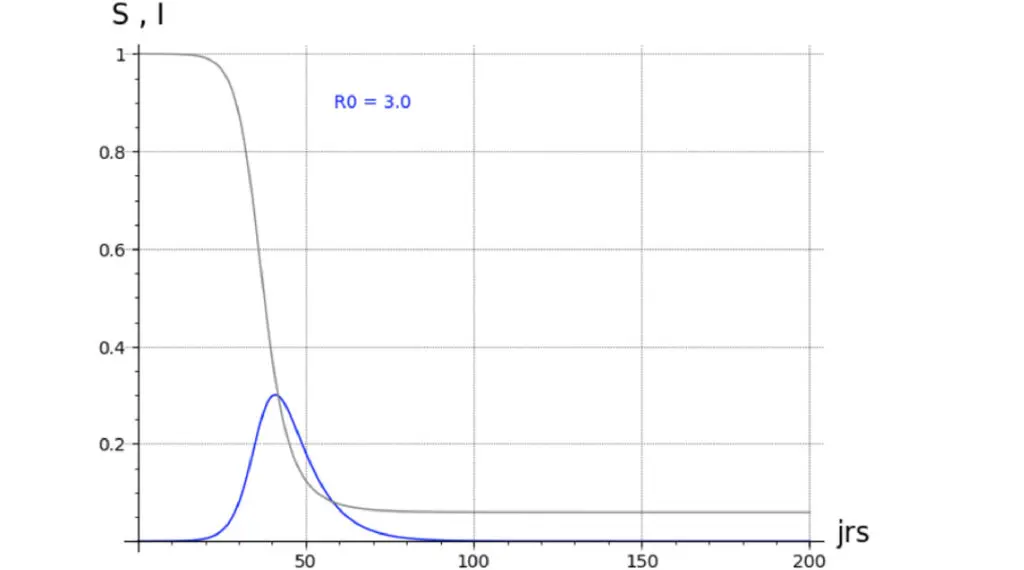
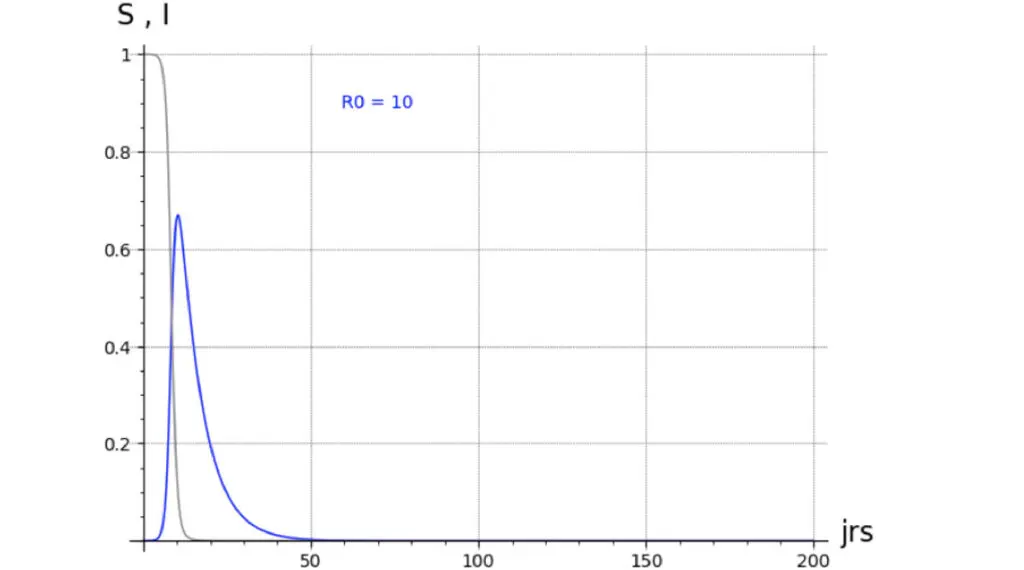
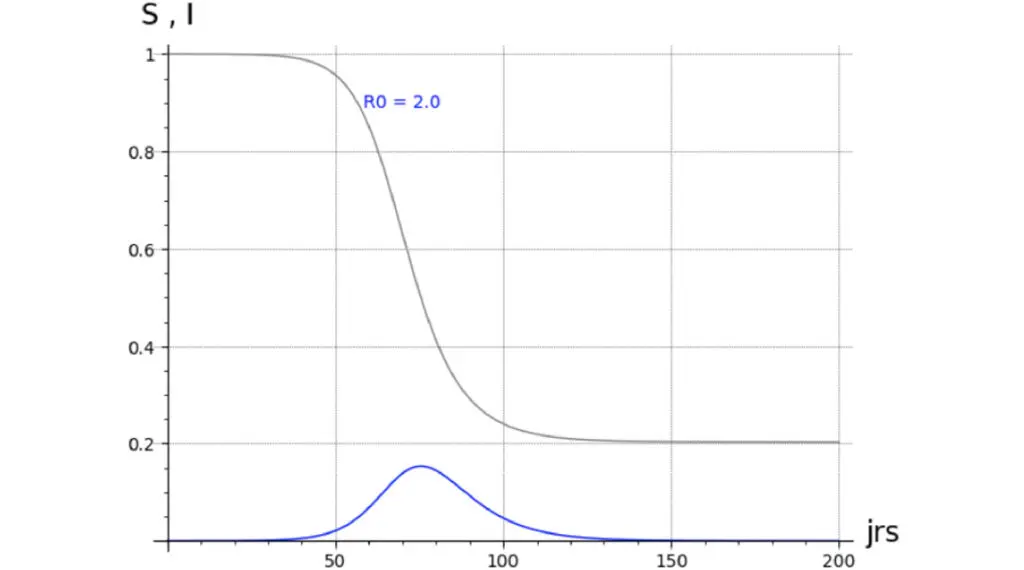
Les autres paramètres sont les mêmes, à savoir :

• Ti égal à 7 (IAV par exemple) ;
• S° étant la pro­por­tion de sus­cep­ti­bles dans la pop­u­la­tion (N) : S°=100 % (de N) ;
• I° égal à 100/N, N égal à 65E+06.

Ces valeurs ne sont pas celles des paramètres de notre épidémie et ne sont util­isées que pour les besoins du graphique.

Les pre­miers enseigne­ments de ces vari­a­tions sur un même mod­èle à infec­tiv­ités dif­férentes sont les suivants :

• il suf­fit d’une très petite valeur de I° pour infecter une pop­u­la­tion (réputée homogène) ;
• dès que le R° est sig­ni­fi­catif (>3) il reste peu de sus­cep­ti­bles (non-infec­tés) en fin d’épidémie ;
• avec un R° pas très grand (1< R° <3) et un petit I°, il faut un temps non nég­lige­able pour que l’épidémie atteigne son pic.

Avec ce pre­mier vocab­u­laire acquis pour par­ler la langue des Zateurs, plusieurs débats s’ouvrent tout seuls :

• le pic de notre épidémie, même si on ne le con­naît pas pré­cisé­ment (aux alen­tours de début avril 2020), n’a pas l’air d’avoir eu besoin de beau­coup de mois pour être atteint… ce qui devrait nous inciter à penser que son R° n’est pas franche­ment petit ;
• et pour­tant on n’arrive même pas à trou­ver 10 % de la pop­u­la­tion infec­tée… alors que, avec un R° un peu mus­clé, la pop­u­la­tion en très grande majorité devrait être sinon immu­nisée, du moins avoir « ren­con­tré » le virus…

Encore un loup !

La seule solu­tion : engager un début de dia­logue avec les Zateurs, mal­gré notre vocab­u­laire basique, et petit à petit con­fron­ter nos don­nées sur les décès avec leurs modèles.

Les bases pour entamer le dialogue avec les habitants de la cité modèle

Sur quelles bases sta­bles pou­vons-nous engager le dia­logue à ce stade ?

• Les décès par 24h à l’hôpital sont des don­nées (les seules) que l’on peut con­sid­ér­er comme pertinentes,
• la durée pour un indi­vidu entre le début de l’apparition des symp­tômes et le moment où on ne con­state plus d’infection est en moyenne entre 14 et 28 jours. La péri­ode de latence est a pri­ori inférieure à 4 jours. On peut donc faire une hypothèse raisonnable au sujet de Ti.

Que dire de la létal­ité (% des décès des per­son­nes infec­tées) de la « bestiole » ?

Là encore, les débats sont nom­breux : 3 % dit-on dans un pays, 1 % dit un autre, 0,53 % dit l’Institut Pas­teur à par­tir des don­nées col­lec­tées à bord du Dia­mond Princess (un échan­til­lon qui certes com­porte des biais mais du moins est util­is­able) ou encore un taux net­te­ment plus faible que 0,5 % ?

Et tout cela en sup­posant que la pop­u­la­tion est homogène, alors que les vieux (à quel âge est-on vieux ? vaste ques­tion …) ont des taux de létal­ité plus élevés…

Inca­pables de tenir un lan­gage clair sur la létal­ité à ce stade, et pour les besoins de ce pre­mier dia­logue, nous fer­ons comme si la létal­ité était de l’ordre de 0,5 %. (Nous avons adop­té le taux de 0,546 % pour nos cal­culs initiaux).

Pour les décès, nous avons retenu le 19 févri­er comme orig­ine des temps.

Pour Ti nous avons retenu la plage de valeurs entre 14 et 32, les infec­tés non passés par l’hôpital se situ­ant plutôt vers 14 et les autres vers 32. Nous fer­ons donc vari­er Ti entre ces valeurs lors de nos rap­proche­ments suc­ces­sifs entre les décès et les modèles.

Le dialogue s’engage : rapprochement avec les décès du 19 février au 3 avril

La courbe des décès se déduisant des infec­tions par pro­por­tion­nal­ité du taux de létal­ité, nous avons demandé à nos inter­locu­teurs Zateurs de con­venir du même taux de létalité.

Nous sommes alors con­venus sans trop de dif­fi­culté, grâce sans doute à notre com­préhen­sion meilleure de la langue des Zateurs, d’effectuer ce rap­proche­ment pour les décès entre le 19 févri­er et le 3 avril. Par con­tre, n’ayant pas du tout les mêmes rites religieux qu’eux, nous avions du mal à nous représen­ter leur dieu R° (dont on a vu plus tôt qu’il était mul­ti­formes), c’est pourquoi nous avons choisi de l’examiner sous toutes ses cou­tures de la valeur 3 jusqu’à la valeur 11.

Un ter­rain d’entente com­mun n’était pas acquis d’avance, mais nous avons finale­ment mis en évi­dence que, sur la plage des valeurs retenues pour Ti, il existe une plage de pos­si­bil­ités pour les dif­férents vis­ages du dieu R° qui se restreint : R° ne peut guère descen­dre en-dessous de 3,6 et non plus se situer bien au-delà de 7,3.

Les voies de R° ne seraient-elles plus aus­si impénétrables ?

Un loup est encore apparu (ça va finir en meute, je vous le dis) : le paramètre S° cen­sé représen­ter la pop­u­la­tion des sus­cep­ti­bles à l’origine est, dans tous ces cas de R°, net­te­ment plus faible qu’imaginé …

Bon ! ça a le mérite d’être com­pat­i­ble avec le faible nom­bre d’infections iden­ti­fiées sur le ter­rain, mais nos inter­locu­teurs étaient pass­able­ment inter­loqués, au point d’envisager de rompre les palabres !

Par chance nos Zateurs étaient dans l’ensemble très polis et, comme nous ne souhaitions pas inter­rompre le dia­logue, nous sommes con­venus que nous dis­cu­te­ri­ons de ce point ultérieurement.

Et si … ?

Et si… on essayait un rapprochement avec les décès du 19 février au 1^er juillet

Tous nos diplo­mates étaient sur le pont : com­ment émet­tre cette idée sans un clash retentissant ?

En effet, la ques­tion posée était : existe-t-il un vis­age du dieu R° com­pat­i­ble, non seule­ment avec l’égalité des décès du 19 févri­er au 3 avril, mais car­ré­ment du 19 févri­er jusqu’au 1^er juil­let alors même que ces décès sont sup­posés avoir été impactés par le confinement ?

Nous nous sommes arrêtés au 1^er juil­let car au-delà les don­nées sont faibles et prob­a­ble­ment liées à des super­po­si­tions de phénomènes très locaux qui ne suiv­ent plus l’évolution générale (comme le clapot vous dis-je…).

Pour ce faire, nous avons directe­ment effec­tué ce rap­proche­ment sur les don­nées réelles des décès sur la total­ité de cette période.

Nous avons con­tin­ué notre dia­logue avec les Zateurs. Le résul­tat était bien évidem­ment incertain.

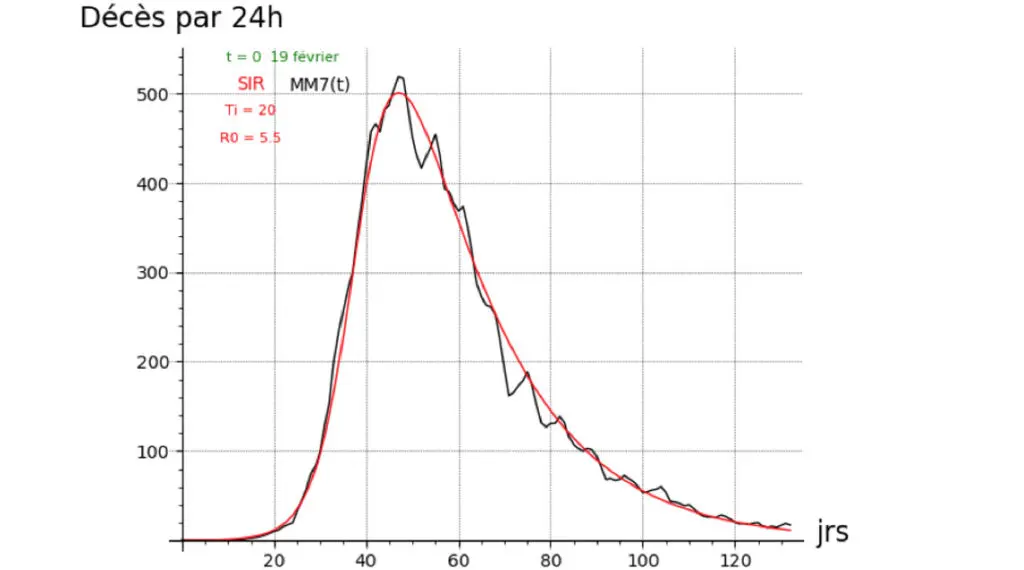
Nous avons donc recher­ché dans le spec­tre des valeurs de R°, celle(s) qui per­me­t­taient de rap­procher les don­nées de décès entre réel et modèle(s).

Le chemin vers R° fut laborieux mais à un moment il s’est éclairé et nous avons trou­vé un vis­age très net du dieu R° qui était com­pat­i­ble de manière opti­male avec cette poten­tielle hérésie con­sis­tant à dire que les décès réels et ceux d’un mod­èle sont iden­tiques sur la péri­ode allant du 19 févri­er au 1^er juillet.

Le tra­vail effec­tué, et après de longues pal­abres encore, nous pou­vons vous livr­er le résul­tat dans les illus­tra­tions ci-dessous, avec les don­nées réelles des décès en moyenne mobile 7 jours (Illus­tra­tion 3.1) et avec les don­nées brutes des décès (Illus­tra­tion 3.2).

Il existe en effet un ensem­ble de valeurs pour les paramètres Ti (durée moyenne de l’infection), R° (nom­bre de repro­duc­tion de base) et β (infec­tiv­ité), qui per­me­t­tent d’approcher de manière opti­male l’ensemble du spec­tre des décès par 24h du 19 févri­er au 1^er juil­let par un mod­èle SIR.

Le dieu R° a main­tenant un vis­age (« le Mod­èle ») : R° = 5.5, Ti = 20 et β = 1.53 E‑06

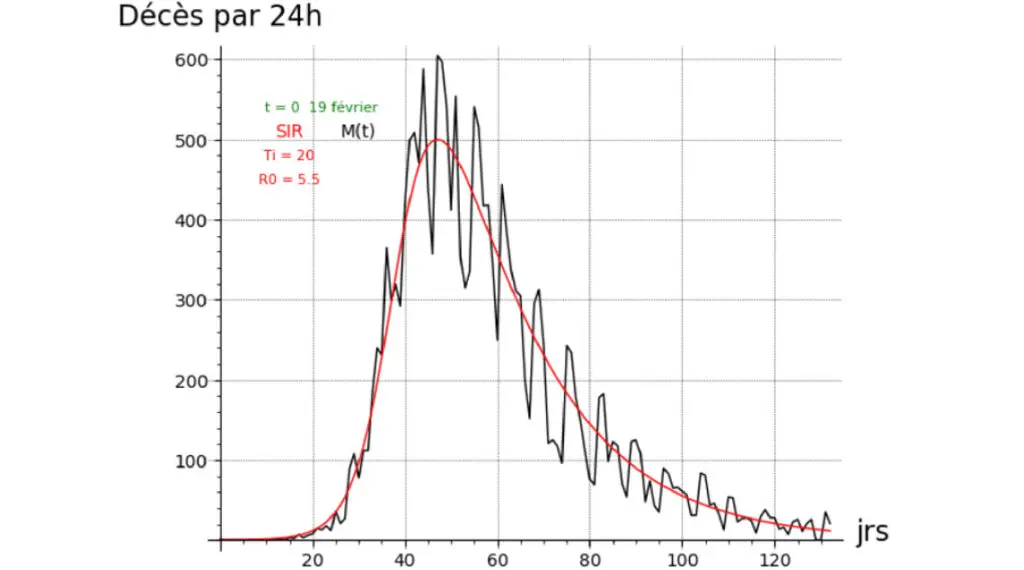
Pour mémoire, les autres paramètres util­isés sont un taux de létal­ité Alfa = 0,546 % et un nom­bre de cas infec­tés à l’origine I° = 28

Les Zateurs se tenaient cois, la bouche ouverte, et nous-mêmes oblig­és d’avouer que « le mod­èle » approchait les décès réels de manière bien plus com­plète que nous avions réus­si à le faire lors de nav­i­ga­tions précé­dentes… Bref tout le monde était silencieux.

En effet, l’épidémie aurait suivi un cours indépen­dant de toute mesure de confinement !

À ce moment pré­cis, ils sont tous apparus… la meute au grand complet !

Et c’est là que la chas­se aux loups a vrai­ment commencé.

Avant la chasse on fourbit ses armes 

Avant de par­tir pour une telle battue, il importe de bien four­bir ses armes…

a) Les données pertinentes sont toujours les décès par 24h à l’hôpital et la sous-population correspondante.

Les élé­ments que l’on peut con­sid­ér­er comme acquis, suite à notre nav­i­ga­tion au pays des mod­èles sont les suivants :

b) Il existe un modèle SIR (« le modèle ») pour lequel les décès suivent avec une excellente adéquation la courbe des décès réels par 24h à l’hôpital sur la quasi-totalité de la période de l’épidémie, à savoir du 19 février au 1^er

c) Les paramètres principaux de « le modèle » sont les suivants :

• Durée moyenne de l’infection au sein d’un individu :

Ti = 20 jours

• Nom­bre de repro­duc­tion de base :

R° = 5,5

• Coef­fi­cient d’infectivité :

β = 1,53 E‑06

Les valeurs de Ti et de R° sont par­faite­ment plau­si­bles, pas de loup de ce côté-là.

En ce qui con­cerne le coef­fi­cient d’infectivité, ce chiffre ne sem­ble pas inco­hérent avec les valeurs pub­liées (entre 1.0E-05 et 1.0E-07) pour des virus con­nus (Influen­za A Virus en particulier…).

La chasse au(x) loup(s)

Réca­pit­u­lons main­tenant nos ren­con­tres avec les loups :

1) Si « le mod­èle » (cf. illus­tra­tion 6.1) est per­ti­nent, alors le con­fine­ment en tant que tel n’a pas eu d’influence sur l’évolution des décès par 24h à l’hôpital.

Les mesures « bar­rières » recom­mandées deux­ième quin­zaine de févri­er ont-elles été suff­isantes pour déter­min­er cette évolution ?

Le déclenche­ment du con­fine­ment s’est-il situé trop près du pic et donc trop « tar­di­ve­ment » pour avoir une réelle influence ?

2) Si « le mod­èle » (cf. illus­tra­tion 6.1) est per­ti­nent, et avec un taux de létal­ité pris par hypothèse aux alen­tours de 0,5 %, cela sig­ni­fie que la sous-pop­u­la­tion infec­tée asso­ciée aux décès est au moment du pic de l’ordre de 100 000 indi­vidus et la pop­u­la­tion des sus­cep­ti­bles à l’origine de l’ordre de 200 000.

Ces chiffres sont sure­ment inférieurs aux chiffres con­cer­nant la total­ité de la pop­u­la­tion. En effet la sous-pop­u­la­tion asso­ciée à nos décès n’est pas la total­ité de la pop­u­la­tion française, et les chiffres cumulés des décès au sein de la pop­u­la­tion sont plutôt de l’ordre du dou­ble (en inclu­ant EPHAD, EMS et décès « à domicile »).

Cepen­dant, le con­stat est qu’au 16 août 2020 le nom­bre de tests effec­tués est de l’ordre de 5 mil­lions et le nom­bre de cas diag­nos­tiqués et/ou testés est de l’ordre de 240 000.

Bref, la pop­u­la­tion iden­ti­fiée comme ayant été infec­tée est effec­tive­ment faible, voire très faible pour un R° qui est large­ment supérieur à 1.

On peut dès lors « pis­ter » 3 traces de loup :

• une par­tie de la pop­u­la­tion aurait été immu­nisée (?) préal­able­ment et la pop­u­la­tion des « Sus­cep­ti­bles » au sein de la pop­u­la­tion française est inférieure à 1 % ?
• le taux de létal­ité réel est très inférieur à celui pris comme hypothèse (qui est pour­tant en fourchette basse de ce qui a été décrit ici ou là) ?
• un mélange de ces 2 pistes ?

Comment expliquer qu’il y ait aussi peu de cas d’infection identifiés en France ?

Même si les tests virologiques et sérologiques n’ont pas con­cerné la pop­u­la­tion entière, force est de con­stater qu’ils mènent à des hypothès­es sur le nom­bre total de per­son­nes infec­tées de l’ordre de 10 % de la pop­u­la­tion (seule­ment ! devrait-on dire).

La piste con­sti­tu­ant à dire qu’une par­tie de la pop­u­la­tion a réa­gi de manière très rapi­de à l’infection est une autre piste ten­tante : le sys­tème immu­ni­taire inné (cel­lules den­dri­tiques, macrophages, cel­lules NK et neu­trophiles) pour­rait avoir digéré les viri­ons et les cel­lules infec­tées avant même que le sys­tème immu­ni­taire adap­tatif (en par­ti­c­uli­er lym­pho­cytes B, pro­duc­teurs des anti­corps) ait eu le temps d’intervenir (délai entre 5 et 7 jours) ?

Cela pour­rait éventuelle­ment expli­quer pourquoi on déclare « non-infec­tés » des indi­vidus qui ont été infec­tés mais n’ont pas pro­duit d’anticorps (ou en quan­tité non détectable) … mais ceci est une autre his­toire sujette à une autre nav­i­ga­tion que j’ai entre­prise par ailleurs.

3) Si nous lais­sons de côté « le mod­èle », mal­gré sa per­ti­nence, pour adopter un mod­èle SIR qui n’est con­forme aux décès que sur la péri­ode du 19 févri­er au 3 avril, par exem­ple, et en recher­chant le plus petit R° qui con­vient, on trou­ve un R° de 4,65 (tou­jours avec Ti=20) qui ne change pas fon­da­men­tale­ment la nature des loups évo­qués en 2).

On pour­rait cepen­dant imag­in­er que l’évolution suit cette courbe (Ti=20 ; R°= 4.65) jusqu’au 3 avril puis (con­fine­ment oblige) « bas­cule » sur les don­nées de « le mod­èle ». Le loup évo­qué en 1) n’en est alors plus un, le nom­bre de décès cumulés au 1^er juil­let serait alors de 35 000 (par rap­port au réel 19 000) et on en déduirait que le nom­bre de décès directs évités grâce au con­fine­ment s’élève à 15 000 env­i­ron… On demeure bien loin des 300 000 en France ou des 3 mil­lions en Europe !

4) Des mod­èles SIR plus sophis­tiqués con­duiraient à d’autres chiffres ?

Des mod­èles à plusieurs seg­ments de Sus­cep­ti­bles ou à plusieurs seg­ments d’Infectés (asymp­to­ma­tiques) auraient une influ­ence sur la créa­tion de phas­es dif­férentes au cours de l’évolution de l’épidémie mais ne résoudraient guère les loups soulevés en 1) et 2).

5) Des mod­èles encore plus sophis­tiqués (mais ils ont tou­jours une base SIR), mod­èles con­sis­tant à tenir compte de struc­tures de con­tact, par âge, par local­i­sa­tion, ont été util­isés abon­dam­ment… Ils sont de nature à atténuer les gros loups soulevés en 2) en par­ti­c­uli­er en dimin­u­ant la pro­por­tion de Sus­cep­ti­bles à l’origine, mais ne répon­dent pas aux ques­tions soulevées.

6) Alors d’autres mod­èles non con­stru­its sur une base SIR ?

Dans tout ce qui précède, les mod­èles SIR con­sid­érés font l’hypothèse que l’infectivité d’un indi­vidu suit au cours de sa péri­ode de con­ta­giosité une courbe du type :

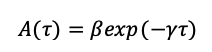
Une autre forme pour l’infectivité A mérit­erait d’être recher­chée et une piste est à suiv­re pour l’identifier.

Pour autant les loups dis­paraitraient-ils pour autant ?

Retour de chasse : une opinion d’honnête homme

Je pour­rais « bris­er là » et m’arrêter sur ce flot de ques­tions non résolues, mais je pense qu’il serait mal­séant, après tous ces efforts de nav­i­ga­tion que vous avez accom­plis avec moi, que je ne vous donne pas mon opin­ion per­son­nelle. Comme d’habitude, elle n’engage que son auteur …

Je vous livre donc mes con­vic­tions ci-après.

• J’ai rarement vu des adéqua­tions aus­si bonnes entre réel et mod­èle sur d’aussi longues péri­odes de temps (comme « le mod­èle » avec les décès) qui ne soient pas per­ti­nentes et sig­nifi­antes. Le mod­èle de cette épidémie est bien un mod­èle de type SIR par­ti­c­uli­er (Ti=20 ; R°=5.5 ; β = 1.53 E‑06).
  Il me reste à effectuer l’analyse cor­re­spon­dante pour les autres pays, mais il est très prob­a­ble qu’ils seront similaires.
• Le con­fine­ment sous sa forme max­i­male déclenché le 16 mars a eu peu d’impact direct sur l’évolution de l’épidémie.
  En par­ti­c­uli­er, les décès cumulés sont qua­si­ment les mêmes avec ou sans ce confinement.
  Il aurait été, par con­tre, dif­fi­cile poli­tique­ment de ne pas pren­dre une telle déci­sion compte tenu des déci­sions déjà pris­es par d’autres pays, de l’explosion pos­si­ble du sys­tème de san­té et des risques de panique et de ten­sions sociales poten­tielle­ment fortes liées à une per­cep­tion de dis­crim­i­na­tion vis-à-vis des accès aux soins.
• Le taux de létal­ité est net­te­ment plus faible qu’annoncé et une par­tie de la pop­u­la­tion n’est pas Susceptible.
• Ce virus est unique en son genre dans son dou­ble con­tourne­ment et détourne­ment de nos défens­es immu­ni­taires, en manip­u­lant notre ADN pour, à la fois dimin­uer l’efficacité de notre réponse immu­ni­taire immé­di­ate (inter­féron) ET exac­er­ber la pro­fu­sion de neu­trophiles et macrophages dans notre organisme.

“Ce virus est unique en son genre dans son double contournement et détournement de nos défenses immunitaires.”

• Nous avons vécu ici et main­tenant une épidémie qui, en ter­mes de pertes humaines, est très min­ime par rap­port au passé (pop­u­la­tions de cer­tains pays ou civil­i­sa­tions réduites de 30 % ! …), mais elle con­stitue une mine d’informations con­sid­érable pour penser un futur, y com­pris, et peut-être surtout, en ter­mes géopolitiques.
  Ce n’est sans doute pas le cas de ce virus, mais, imag­inez que, par nég­li­gence, un virus autrement plus létal que le SARS-CoV­‑2 et bien plus nou­veau (toute la pop­u­la­tion est Sus­cep­ti­ble), s’échappe d’un des mul­ti­ples lab­o­ra­toires mon­di­aux qui les manip­u­lent (au sens pro­pre) à des fins de prévention…
• Je pense égale­ment qu’une analyse fac­to­rielle com­plète (de bons out­ils exis­tent) mérit­erait d’être faite sur les car­ac­téris­tiques com­munes des pays qui ont eu des nom­bres de décès par habi­tants très faibles.
  Ce n’est pas parce qu’on peut penser que cer­tains pays ont eu des compt­abil­i­sa­tions insuff­isantes de ces décès, voire des poli­tiques volon­taires de sous-déc­la­ra­tion, qu’on n’en tir­erait pas des enseigne­ments très intéressants.

Bibliographie / Références

[1] https://dashboard.covid19.data.gouv.fr/vue-d-ensemble?location=FRA

[2] Ker­ma­ck (W. O.) and McK­endrick (A. G.) (1927), « Con­tri­bu­tions to the math­e­mat­i­cal the­o­ry of epi­demics », part I. Pro­ceed­ings of the Roy­al Soci­ety A 115, 700–721, Reprint­ed : Bul­letin of Math­e­mat­i­cal Biol­o­gy (1991), 53, 33–55.

[3] Heester­beek (J.A.P.) and Dietz (K.) (1996) The con­cept of R° in epi­dem­ic the­o­ry, Sta­tis­ti­ca Neer­landi­ca (1996) Vol. 50, nr. 1, pp. 89–110

[4] Maniv­el (C.) COVID-19 : Déter­mi­na­tion des paramètres R°, β et γ d’un mod­èle SIR de l’épidémie à par­tir des décès à l’hôpital sur la péri­ode en France du 19 févri­er au 1^er juil­let 2020 HAL Id : 02923715

---

Articles similaires :

Mod­èles math­é­ma­tiques d’épidémies les plus élaborés : pourquoi leurs prévi­sions ini­tiales sont-elles sou­vent exces­sive­ment pessimistes ? Covid-19 : une mod­éli­sa­tion sim­ple util­isant Excel, acces­si­ble aux non-math­é­mati­ciens et pleine d’enseignements « Deux­ième vague » Covid-19 : per­spec­tives 2020–2021 Covid-19 : inter­ro­ga­tions sur le mod­èle épidémi­ologique,
Prise en compte de la vac­ci­na­tion et du « vari­ant anglais » Les héros dis­crets de la crise de la Covid Une expéri­ence con­crète en milieu hos­pi­tal­ier : l’Hôpital améri­cain de Paris