Structures dans l’Ensemble de Mandelbrot

J’ai décou­vert l’En­semble dans les articles de Dewd­ney, mais faute d’or­di­na­teur per­son­nel je n’en ai rien tiré à l’é­poque. C’est la ren­contre for­tuite avec le pro­gramme Chaos qui a relan­cé mon inté­rêt en 1993, et cette fois j’ai déci­dé de ne pas en res­ter à l’exa­men aléa­toire d’i­mages belles mais incompréhensibles.

Adop­tant l’ap­proche métho­do­lo­gique de Man­del­brot, et m’ap­puyant sur des mathé­ma­tiques de taupe acces­sibles à tous, j’ai pous­sé l’a­na­lyse des images bien au-delà de tout ce qui avait été fait jus­qu’à pré­sent, et trou­vé les lois, extrê­me­ment simples et géné­rales, qui régissent la struc­ture de l’Ensemble.

Cette décou­verte, véri­fiée sur un très grand nombre de cas (lit­té­ra­le­ment plus de 10 000), reste une simple conjec­ture car je n’ai pas trou­vé de démons­tra­tion. J’es­père convaincre les mathé­ma­ti­ciens de s’y intéresser.

En atten­dant, elle per­met à tout un cha­cun, uti­li­sant le pro­gramme Chaos et quelques addi­tions de mon cru, de com­prendre la struc­ture de n’im­porte quelle image, et d’en pré­dire quan­ti­ta­ti­ve­ment les carac­té­ris­tiques, jus­qu’aux plus infimes détails acces­sibles (gros­sis­se­ment 10¹⁴ environ).

Rappels

Pour situer les décou­vertes, il faut rap­pe­ler ce qui était connu en 1993 en matière de struc­ture de l’En­semble. J’es­saye d’être bref, mais il faut que la suite soit compréhensible.

Définition

L’En­semble de Man­del­brot est l’en­semble des points C du plan com­plexe qui font conver­ger l’itération :

Z_n+1 = Z_n² + C, avec Z_o = 0.

On démontre aisé­ment que l’En­semble est symé­trique par rap­port à l’axe hori­zon­tal, et inté­rieur au cercle de rayon 2 cen­tré sur l’o­ri­gine. On défi­nit alors la diver­gence comme le fran­chis­se­ment de ce cercle.

L’al­go­rithme de Man­del­brot consiste à colo­rier en noir les points C de l’En­semble, et en cou­leurs les points qui conduisent à une diver­gence. Une cou­leur spé­ci­fique est asso­ciée à chaque valeur pos­sible (pla­fon­née arbi­trai­re­ment pour limi­ter la durée des cal­culs) du nombre d’i­té­ra­tions effec­tuées au moment de la diver­gence. Le choix de cette cor­res­pon­dance pré­sente un grand inté­rêt sous l’angle esthé­tique, évi­dem­ment, mais aus­si pour les mathé­ma­ti­ciens. Le choix que j’ai fait dans Chaos éta­blit un net contraste à la fron­tière de l’En­semble, mar­quée par des cou­leurs claires : il est pri­mor­dial pour la com­pré­hen­sion des structures.

Domaines

La pré­sen­ta­tion des résul­tats à l’é­chelle 1 (le cercle de rayon 2 rem­plis­sant l’é­cran) met en évi­dence trois domaines dont l’é­tude mathé­ma­tique révèle les spé­ci­fi­ci­tés (figure 1).

Cette zone déli­mi­tée par une car­dioïde, dont le point de rebrous­se­ment est à + 0,5 et le som­met à – 0,75, est le domaine de conver­gence vraie : à chaque valeur de C cor­res­pond une limite A que l’on sait cal­cu­ler direc­te­ment. Le contour de la car­dioïde appar­tient au domaine. L’o­ri­gine est sa propre limite.

À l’ex­té­rieur de la car­dioïde la conver­gence change de nature : il n’y a pas une limite, mais un groupe de p valeurs for­mant cycle, dont p est la période. À chaque valeur de C cor­res­pond un jeu unique de valeurs et une période spécifique.

Le domaine 2 se com­pose d’une infi­ni­té de sous-domaines d’ap­pa­rence cir­cu­laire, tan­gents à la car­dioïde ou entre eux. À l’in­té­rieur d’un sous-domaine, la période est la même en tous points, et j’ap­pelle poids du sous-domaine cette période commune.

Je bap­tise » cercles » ces sous-domaines, bien que la preuve de cir­cu­la­ri­té n’existe que pour le gros cercle axial ; des mesures sur cer­tains autres montrent que l’é­cart à la cir­cu­la­ri­té, s’il existe, est infé­rieur au dix mil­lième. On peut clas­ser ces cercles comme suit :

a) une famille pri­maire, symé­trique par rap­port à l’axe hori­zon­tal, com­men­çant avec le cercle axial de poids 2 (noté C2), et se pour­sui­vant avec des paires de cercles de poids 3 (C3, en haut et en bas), 4 (C4, à 45° du côté droit), 5, 6 (C6, tan­gents à droite de la car­dioïde), etc., jus­qu’à l’in­fi­ni dans le point de rebroussement.

b) entre deux cercles pri­maires quel­conques de poids p et p + 1 existe une série secon­daire, avec un cercle secon­daire majeur situé à peu près au milieu, de poids 2 p + 1, et deux séries infi­nies M et P qui l’en­cadrent. Par exemple, il existe une paire de CS5 à 45° entre C2 et C3, pour p = 2.

c) on défi­nit ensuite de la même manière, et on observe, des séries ter­tiaires, qua­ter­naires, qui­naires, etc., jus­qu’à l’in­fi­ni. Le poids de cha­cun de ces cercles s’é­va­lue de proche en proche en fonc­tion du p ini­tial, par simple addi­tion des poids des cercles enca­drants. Tous les cercles com­pris entre Cp et Cp + 1 ont ain­si un poids m de la forme a p + b : nous décou­vri­rons plus loin l’im­por­tance du coef­fi­cient a.

On sait cal­cu­ler les coor­don­nées du point de contact de cha­cun de ces cercles avec la car­dioïde, et la tan­gente en ce point, qui sépare le domaine de poids 1 du sous-domaine de poids m.

Autour de cha­cun de ces cercles de pre­mier niveau existe une hié­rar­chie de familles subor­don­nées, dont le numé­ro se cal­cule comme les poids ci-des­sus. Le poids de cha­cun de ces cercles de 2^e niveau est le pro­duit de son numé­ro par le poids du cercle porteur.

Cette pro­prié­té est récur­sive, et il existe des cercles de 3^e, 4^e niveau, etc., jus­qu’à l’in­fi­ni. Sur l’axe, par exemple, il existe une infi­ni­té de cercles de poids 2, 4, 8, 16, etc.

Des for­mules existent pour déter­mi­ner le point de contact de chaque cercle avec son por­teur. Cepen­dant, seul le cas du por­teur C2 est acces­sible en bloc à l’or­di­na­teur. Pour les autres, le cal­cul est numé­rique et point par point.

À l’ex­té­rieur des domaines 1 et 2 join­tifs, on observe des points noirs de conver­gence, en appa­rence non connec­tés. En gros­sis­sant ces points, on constate que cha­cun d’eux est une copie approxi­ma­tive de l’en­semble com­plet : on démontre que la cor­res­pon­dance est un homéo­mor­phisme, qui conserve toutes les pro­prié­tés décrites ci-des­sus, tout en auto­ri­sant des défor­ma­tions, notam­ment en torsion.

On a démon­tré que l’En­semble est connexe. Il faut donc trou­ver la struc­ture qui intègre les micro­car­dioïdes du domaine 3 avec les domaines 1 et 2.

Le nombre des objets de poids p, cercles ou micro­car­dioïdes, est bor­né par le nombre 2^p‑1 – 1. Mais, puisque p peut croître indé­fi­ni­ment, le nombre des cercles et le nombre des micro­car­dioïdes de l’en­semble sont tous deux infinis.

Rosaces

Une image de l’En­semble (figure 1) montre la zone noire entou­rée d’une frange colo­rée. En gros­sis­sant un point quel­conque de cette frange, on découvre qu’elle est consti­tuée de des­sins dis­joints, cha­cun éma­nant d’un cercle.

Une pro­prié­té remar­quable, non démon­trée mais géné­rale, est que le des­sin issu d’un cercle de poids p est une rosace à p bras, dont un pédon­cule rat­ta­chant le cœur de la rosace au cercle. Nous notons B1 le pédon­cule, B2 à Bp les bras libres.

Chaque bras libre sert lui-même de B1 à une rosace ter­mi­nale Rp à p bras, et cela récursivement.

On constate que les micro­car­dioïdes sont exclu­si­ve­ment loca­li­sées dans les bras, ce qui sug­gère que la topo­lo­gie de l’En­semble est en étoile.

Les textes mathé­ma­tiques ne parlent que peu de ces des­sins, qu’ils bap­tisent « antennes », de sorte qu’il est dif­fi­cile de sépa­rer ce qui était connu avant que j’é­tu­die ces des­sins, de ce qui ne l’é­tait pas. Je dirai seule­ment que je n’ai trou­vé dans aucun texte une quel­conque allu­sion à la struc­ture interne des rosaces. Je suis donc seul res­pon­sable de ce qui suit.

Bras

Un bras est une struc­ture linéaire s’é­ten­dant entre deux points asymp­totes (PA), qui sont des cœurs de rosaces, prin­ci­pale ou ter­mi­nale. Chaque bras contient une infi­ni­té de micro­car­dioïdes, par­mi les­quelles une pré­sente le poids mini­mum : cette micro­car­dioïde est la majeure du bras, et par défi­ni­tion exten­sive le poids du bras est celui de sa micro­car­dioïde majeure.

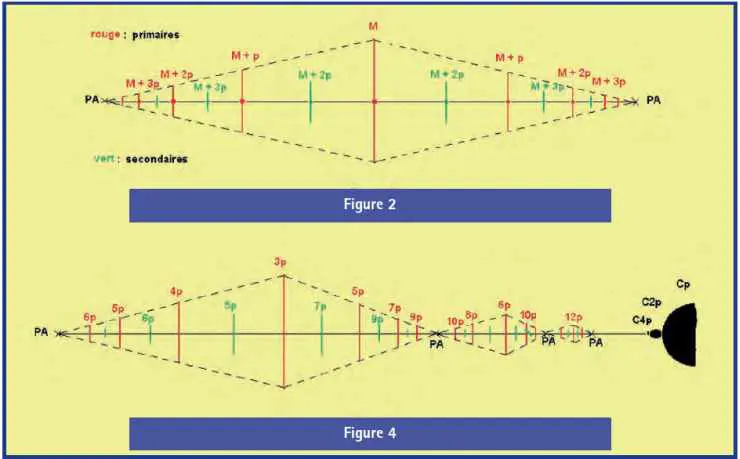
La répar­ti­tion des micro­car­dioïdes dans les bras libres est de type binaire : une car­dioïde M au centre approxi­ma­tif, enca­drée de deux car­dioïdes de poids M + p, quatre M + 2p, huit M + 3p, etc. (figure 2).

La taille et l’es­pa­ce­ment des micro­car­dioïdes du bras dimi­nuent très rapi­de­ment quand le poids aug­mente, pour se sta­bi­li­ser sur une loi logarithmique :

Log taille(A) – Log taille(B) = k (poids(B) – poids(A))
mais le coef­fi­cient k n’a de valeur que locale, déter­mi­née au mieux pour un demi-bras, amont ou aval.

Avec une telle loi, les car­dioïdes M + kp, avec k = 0 à 5 pour fixer les idées, occupent la plus grande part de la lon­gueur du bras, et les autres, vers les extré­mi­tés, ne deviennent visibles qu’en gros­sis­sant l’en­tou­rage des points asymptotes.

Les poids des bras libres d’une rosace Rp sont tous dif­fé­rents : ces bras se par­tagent des poids p + 1 à 2p – 1. L’at­tri­bu­tion des poids aux bras ne se fait pas dans l’ordre des numé­ros, mais selon une hié­rar­chie propre à la famille du cercle :

– le pas hié­rar­chique est 1 dans les séries pri­maires, c’est-à-dire que la hié­rar­chie s’y confond avec le numérotage,
– le pas hié­rar­chique est 2 dans les secon­daires majeurs,
– pour tous autres cercles de poids m = ap + b, le pas hié­rar­chique est le coef­fi­cient a.

Les bras sont construits comme un enchaî­ne­ment de maillons, qui dans les bras libres appa­raissent au pre­mier abord comme des tri­plets : deux rosaces majeures Rp enca­drant une croix. La croix est défi­nie comme une car­dioïde por­tant deux rosaces laté­rales Rp, atta­chées par un bras laté­ral à ses cercles C3 (figure 3).

Les pédon­cules ont une struc­ture tout à fait par­ti­cu­lière (figure 4) :

a) ils sont stric­te­ment rec­ti­lignes, du cercle au PA cœur de la rosace principale ;

b) ils ne sont pas symé­triques lon­gi­tu­di­na­le­ment. Leur majeure est 3p, et le pas aval est p comme dans les bras libres, mais le pas amont est 2p. Cette pre­mière sec­tion est le pédon­cule propre du cercle Cp. À l’a­mont du pédon­cule 3p, on trouve dans son pro­lon­ge­ment un bras 6p, puis un bras 12p, etc. : ce sont les pédon­cules des des­sins asso­ciés aux cercles C2p, C4p, … qui existent néces­sai­re­ment entre Cp et sa rosace, même si on ne les dis­tingue pas à l’é­chelle de la rosace prin­ci­pale Rp ;

c) les maillons qui les consti­tuent ne sont pas des tri­plets, mais seule­ment des croix. Les car­dioïdes des pédon­cules s’at­tachent l’une à l’autre direc­te­ment, sans inter­po­si­tion de rosace.

Capsules

L’ar­bo­res­cence binaire des tri­plets d’un bras libre de rosace Rp se pour­suit indé­fi­ni­ment au pas p, mais elle n’en consti­tue pas l’u­nique struc­ture. Si on exa­mine le détail d’un bras, on observe que les rosaces majeures Rp du tri­plet séparent net­te­ment celui-ci du reste du bras :

– à l’ex­té­rieur de la Rp du tri­plet M com­mence un bras de liai­son qui s’é­tend jus­qu’à la Rp du pri­maire voi­sin M + p. Ce bras est par­ta­gé par les deux rosaces et son poids est M + 2p. Sa des­crip­tion se déduit récur­si­ve­ment de celle du bras M et par­ti­cipe à sa struc­ture (voir figure 2) ;

– entre les cœurs des deux Rp majeures se trouve la struc­ture locale du tri­plet, que nous appel­le­rons sa cap­sule et que nous allons détailler.

Toute car­dioïde est encap­su­lée. Et, puisque la cap­sule contient de nom­breuses micro­car­dioïdes subor­don­nées, sou­li­gnons que cette affir­ma­tion est récur­sive. Moyen­nant quoi, nous pou­vons révi­ser le sché­ma de prin­cipe du bras, tel que décrit plus haut, par quelques chiffres frap­pants, tirés d’un bras par­ti­cu­lier typique :

– la cap­sule du tri­plet majeur occupe envi­ron 45 % de la lon­gueur du bras,

– l’en­semble des cap­sules de la série pri­maire de tri­plets repré­sente 80 % de la lon­gueur du bras,

– la lon­gueur du plus grand bras secon­daire, entre la cap­sule de M et celle de M + p, ne repré­sente que 8 % de la lon­gueur du bras, et non 25 % comme le lais­sait sup­po­ser le sché­ma de prin­cipe, avec ses micro­car­dioïdes ponctuelles.

De tels chiffres montrent que la cap­sule ne peut être igno­rée. Qu’il n’en soit par­lé nulle part sou­ligne que, depuis des années, les cher­cheurs ont aban­don­né les images pour reve­nir à l’abstraction.

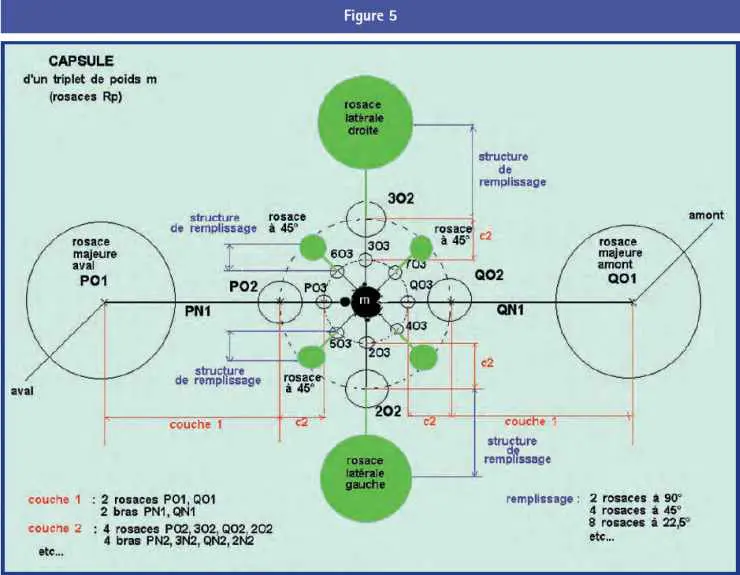
La figure 5 montre l’or­ga­ni­sa­tion de prin­cipe de toute cap­sule, for­mée de couches imbri­quées. Soit M le poids de la car­dioïde cen­trale, tri­plet quel­conque d’un bras de Rp.

Couche 1 : sur le même exemple, cette couche repré­sente 64 % en lon­gueur et 85 % en sur­face de l’en­com­bre­ment total de la capsule.

Le long de l’axe d’ap­proxi­ma­tive symé­trie de la micro­car­dioïde, la couche 1 se com­pose de deux struc­tures de connexion amont et aval, com­po­sées cha­cune d’une des rosaces majeures (moins le bras de liai­son), et d’un bras de connexion qui est d’ailleurs un des bras de la Rp. Ce bras de connexion s’é­tend du cœur de la Rp de couche 1 au cœur de la Rp de couche 2.

Si la car­dioïde M appar­tient à un bras de numé­ro Bi, et si nous nom­mons B1 le bras de liai­son du tri­plet vers l’ex­té­rieur, la rosace majeure Rp com­porte p – 2 bras libres et son bras de connexion est le bras Bi. Les poids des bras libres de la Rp sont déter­mi­nés par les règles hié­rar­chiques nor­males en par­tant de B1 = M + p ; le bras Bi de connexion obéit à des règles par­ti­cu­lières, décrites plus loin.

Sur la direc­tion per­pen­di­cu­laire, maté­ria­li­sée par les cercles C3 de la micro­car­dioïde M, la couche 1 com­prend deux struc­tures de rem­plis­sage droite et gauche (en regar­dant vers l’a­val). Cha­cune de ces struc­tures com­prend une rosace laté­rale avec p – 1 bras libres, et un bras de rem­plis­sage qui des­cend vers la car­dioïde, ter­mi­né par un point asymptote.

L’at­tri­bu­tion de poids à ces divers bras obéit à des règles décrites plus loin. On retien­dra pour le moment que les rosaces laté­rales sont approxi­ma­ti­ve­ment symé­triques par rap­port à l’o­ri­gine de la cardioïde.

Couche 2 : très gros­siè­re­ment, et sim­ple­ment comme ordre de gran­deur, la couche 2 occupe à l’in­té­rieur de la couche 1 la même place rela­tive que celle-ci dans l’en­semble de la capsule.

Elle com­prend quatre struc­tures de connexion iden­tiques, déduc­tibles l’une de l’autre par rota­tion d’en­vi­ron 90° autour de la car­dioïde cen­trale, dont les rosaces forment point asymp­tote inté­rieur pour les bras de connexion et les bras de rem­plis­sage de la couche 1.

Ces struc­tures de connexion se déduisent par simi­li­tude des struc­tures de couche 1, avec tous les poids aug­men­tés de M. La rela­tion loga­rith­mique entre poids et taille explique la consi­dé­rable dimi­nu­tion des dimen­sions, d’une couche à la suivante.

À 45° de ces quatre struc­tures appa­raissent quatre struc­tures de rem­plis­sage, elles aus­si déduites par simi­li­tude des struc­tures de couche 1 avec poids aug­men­té de M. Ces struc­tures émanent de points bien défi­nis de la car­dioïde, nom­mé­ment les cercles C2.3 et C4.

Exemple figure 5A

Couche 3 : huit struc­tures de connexion de poids encore accru de M s’at­tachent à l’in­té­rieur des huit struc­tures de couche 2. Huit struc­tures de rem­plis­sage s’in­ter­calent entre elles, éma­nant de huit points bien défi­nis de la micro­car­dioïde centrale.

Ce dis­po­si­tif se pour­suit indé­fi­ni­ment, par dou­ble­ment du nombre des struc­tures à chaque couche. Des mesures ont été effec­tuées jus­qu’à la couche 100 sur la car­dioïde C2. B2MK de poids 3, la plus grosse de l’en­semble. Les points d’at­tache des struc­tures de rem­plis­sage ont été déter­mi­nés jus­qu’à la couche 13 (4 096 points d’at­tache propres).

Dès la couche 6, la forme des enve­loppes cesse d’être qua­si cir­cu­laire pour se mode­ler sur la forme de la micro­car­dioïde, l’é­pais­seur des couches conti­nuant à dimi­nuer dans un rap­port de l’ordre de 2,6 avec leur rang. De la sorte, il existe une limite à dis­tance finie, que nous appe­lons la couche d’i­so­le­ment : c’est l’en­semble de tous les points asymp­totes ter­mi­nant tous les bras de toutes les rosaces de la micro­car­dioïde, homéo­mor­phisme de la limite qui sépare l’En­semble de la zone de divergence.

Structures de connexion – Évocation amont

L’ex­po­sé pré­cé­dent montre qu’il suf­fit de connaître la struc­ture de connexion de couche 1 pour connaître l’en­semble de la cap­sule. Le poids des car­dioïdes du bras de connexion de couche 1 est déter­mi­né par évo­ca­tion amont, laquelle fonc­tionne comme suit :

Soit m le poids d’une car­dioïde quel­conque, pri­maire au sein d’un bras de poids M, déli­mi­té par deux points asymp­totes dont l’un est for­cé­ment à l’a­mont de m ;

1) exa­mi­ner toutes les car­dioïdes entre m et ce PA amont, soit a le plus petit poids ren­con­tré. a est le para­mètre d’é­vo­ca­tion amont de la car­dioïde m, et le tri­plet majeur du bras de connexion de couche 1 aura un poids m + a ;

2) exa­mi­ner toutes les car­dioïdes entre m et a, soit q1 le plus petit poids ren­con­tré, for­cé­ment > a. S’il existe plu­sieurs car­dioïdes de poids q1 entre m et a, on choi­si­ra la plus proche de m. Le deuxième tri­plet du bras de connexion de couche 1 aura un poids m + q1 ;

3) recom­men­cer cette recherche entre m et q1 pour trou­ver q2 > q1 et obte­nir un tri­plet de couche 1 de poids m + q2. Cet exer­cice se pour­suit tant que qi < a + m, car nous savons d’a­près les défi­ni­tions que la couche 2 com­mence par un poids (m + a) + m ;

4) ain­si le bras de connexion contient un maxi­mum de m car­dioïdes pri­maires, de poids com­pris entre m + a et 2m + a – 1. L’en­semble de ces poids consti­tue le code carac­té­ris­tique de la car­dioïde m ; il est unique au sein du bras M ;

5) entre deux pri­maires m + qi et m + qi + 1 ain­si défi­nis, il existe des secon­daires de poids supé­rieur. Ce sont des évo­ca­tions des secon­daires situés entre les car­dioïdes amont qi et qi + 1.

Si le bras M est un bras de rosace prin­ci­pale, toutes les car­dioïdes sus­cep­tibles d’être uti­le­ment évo­quées ont des poids de la forme M + k p. Les poids de couche 1 de m sont alors de forme m + a + i p.

Mais le prin­cipe d’é­vo­ca­tion amont a une por­tée plus géné­rale. Il s’ap­plique à toute car­dioïde m interne au bras M, par exemple une car­dioïde d’un bras quel­conque d’une rosace ter­mi­nale, ou une car­dioïde de cap­sule. L’ex­plo­ra­tion décrite plus haut fran­chi­ra alors néces­sai­re­ment un ou plu­sieurs PA, cœur de rosace ter­mi­nale ou cœur de rosace de cap­sule. À chaque tra­ver­sée de ce genre, la séquence au pas p est inter­rom­pue pour reprendre le cal­cul de la couche 1 avec une nou­velle origine.

Il est alors néces­saire d’in­tro­duire dans le bras de connexion une rosace inter­mé­diaire, évo­ca­tion de la rosace tra­ver­sée dont elle reco­pie­ra la dis­po­si­tion des bras. Le code doit incor­po­rer ces rosaces, et la cap­sule est dite feuille­tée.

Le feuille­tage est extrê­me­ment répan­du, et la struc­ture des cap­sules se com­plique donc au fur et à mesure que l’on explore plus de détails. Cette pro­prié­té des struc­tures mathé­ma­tiques abs­traites les dis­tingue défi­ni­ti­ve­ment des struc­tures du monde phy­sique, qui finissent tou­jours – croit-on – par atteindre un niveau ultime, ato­mique au sens étymologique.

Structures de remplissage – Évocation aval

L’ex­po­sé sur les cap­sules a mon­tré que la connais­sance de la struc­ture de rem­plis­sage de couche 1 suf­fit pour connaître toutes les struc­tures de ce type dans la capsule.

Le poids des car­dioïdes du bras de rem­plis­sage est déter­mi­né par évo­ca­tion aval. On ne repren­dra pas le détail du pro­cé­dé, qui exa­mine cette fois l’in­ter­valle sépa­rant la car­dioïde m du PA aval du bras M, et per­met de défi­nir un para­mètre b d’é­vo­ca­tion aval, qui n’a aucune rai­son d’être égal au para­mètre a d’é­vo­ca­tion amont, sauf si m = M.

L’é­vo­ca­tion ne s’ar­rête pas au PA, cepen­dant. Au-delà de ce PA, il existe dans le bras M une récur­sion illi­mi­tée de rosaces ter­mi­nales, et la rosace laté­rale de m n’est autre que l’é­vo­ca­tion de cette ter­mi­nale. En résu­mé donc, l’en­semble de la struc­ture de rem­plis­sage est l’é­vo­ca­tion, par trans­la­tion m de tous les poids, de tout ce qui existe dans le bras M à l’a­val de la car­dioïde m.

Conséquences

Les méca­nismes expo­sés sont rela­ti­ve­ment simples, et je les ai appli­qués pour une étude métho­dique de deux bras par­mi l’in­fi­ni­té des possibles :

– le grand bras C2. B2 de poids 3, qui est le bras libre unique de la rosace R2, éma­na­tion du cercle C2. L’é­tude visait à iden­ti­fier indi­vi­duel­le­ment toutes les car­dioïdes de poids infé­rieur ou égal à 20, et à déter­mi­ner leur code caractéristique.

Elle s’est éten­due aux ter­mi­nales suc­ces­sives de poids 4 à 11, qui ont confir­mé de façon par­ti­cu­liè­re­ment convain­cante les pré­vi­sions sur le feuille­tage des capsules.

– le bras CS5. B2 de poids 8, arbi­trai­re­ment choi­si par­mi les quatre bras libres de la rosace du cercle secon­daire CS5, en vue de contrô­ler l’u­ni­ver­sa­li­té des prin­cipes décou­verts dans l’é­tude pré­cé­dente. La limite de poids choi­sie est ici 50, car le pas est 5.

Cette étude a mon­tré qu’il est par­fai­te­ment pos­sible d’é­crire un pro­gramme d’or­di­na­teur pour déter­mi­ner auto­ma­ti­que­ment la struc­ture d’un bras quel­conque, de pas p et de poids M fixés, jus­qu’à une pro­fon­deur (poids maxi­mum) choi­sie a prio­ri. Cepen­dant, ce résul­tat numé­rique ne donne aucune idée de l’as­pect réel des images d’un tel bras.

Je répète que toute car­dioïde est encap­su­lée. On est donc conduit à réflé­chir sur la struc­ture de cap­sules imbriquées.

Ce tra­vail a été pous­sé jus­qu’à ses ultimes consé­quences, et a per­mis d’ex­pli­quer de nom­breuses obser­va­tions a prio­ri bizarres. Je me borne à les énon­cer ; le lec­teur curieux pour­ra soit consul­ter les réfé­rences in fine, soit m’ai­der à orga­ni­ser une pré­sen­ta­tion de dia­po­si­tives ou un cours sur ordinateur :

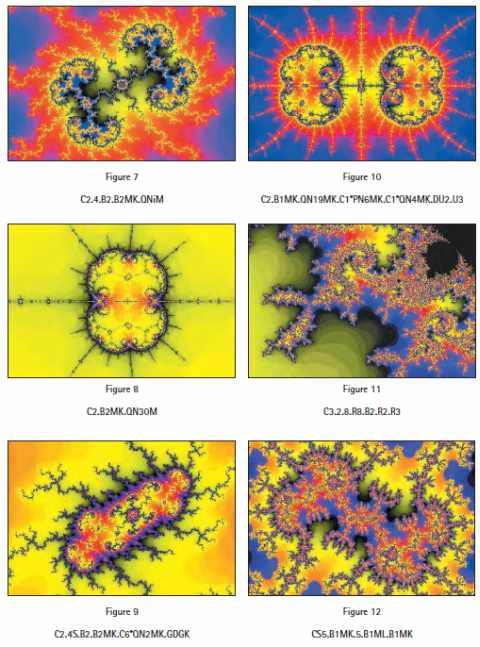
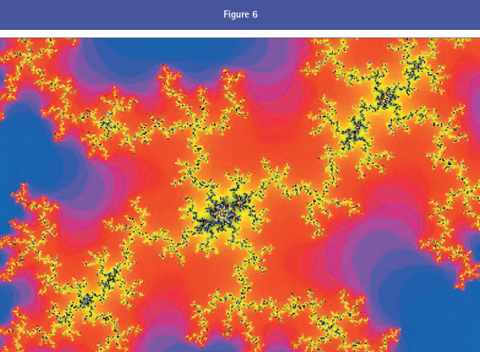
– amas de car­dioïdes résul­tant d’é­vo­ca­tions récur­sives (figures 6 et 7),

– conver­gence vers une struc­ture com­mune de tri­plets de couches pro­fondes dans des cap­sules cor­res­pon­dant à des valeurs dif­fé­rentes de p (figure 8),

– struc­ture remar­quable des car­re­fours dans les arbo­res­cences de tels tri­plets (figure 9),

– appa­ri­tion de struc­tures spé­ci­fiques, récur­sives et sus­cep­tibles de se com­bi­ner, à par­tir du deuxième niveau d’en­cap­su­la­tion. Je les ai bap­ti­sées boules, d’a­près leur forme (figure 10).

Cas des B1 pédoncules

Puis­qu’il n’y a pas de rosace dans les maillons des bras B1 pédon­cules, que devient dans ces bras le concept de capsule ?

a) L’é­vo­ca­tion amont s’ap­plique inté­gra­le­ment, et porte exclu­si­ve­ment sur des car­dioïdes de bras B1, par construc­tion. Mais puisque aucune rosace ne risque de s’in­ter­po­ser et de cou­per les séquences de poids, il est per­mis qu’une car­dioïde par­ti­cu­lière joue deux rôles, pour­vu que son poids l’autorise :

– membre de l’ar­bo­res­cence M + k p des car­dioïdes struc­tu­relles du bras,

– élé­ment d’une couche de capsule.

Cette inter­pé­né­tra­tion est assez fré­quente et com­plique l’a­na­lyse. Elle réduit nota­ble­ment le nombre de car­dioïdes de poids don­né dans un bras B1, par rap­port à un Bi de même poids.

b) L’é­vo­ca­tion aval s’ap­plique éga­le­ment : toutes les rosaces laté­rales des B1 pédon­cules sont donc des évo­ca­tions de la seule rosace visible à leur aval, c’est-à-dire la rosace principale.

c) Les bras B1 des cercles C2p, C4p, etc., en amont du B1 de Cp, évoquent cette même rosace : quel que soit le cercle qui leur cor­res­pond, les croix de ces B1 ont donc des rosaces laté­rales à p bras.

Cercles de niveau supérieur à 1

Consi­dé­rons un cercle Cp tan­gent à la car­dioïde de base, por­tant un cercle Cq qui porte lui-même un cercle Cr. On a déjà indi­qué que le poids de ce der­nier cercle est p q r. Que sont les des­sins éma­nant du cercle Cp.q.r ?

Ce sont des rosaces arbo­res­centes qui expriment, dans l’ordre inverse, les rangs de tous les cercles tra­ver­sés :< ul>

• une rosace de base Rr à r bras dont un pédon­cule de poids p q r , et r – 1 bras libres de poids k1_n1 = p q (r + n1) ;
• sur chaque bras libre de Rr, une rosace Rq à q – 1 bras libres, à laquelle le bras de la Rr sert de B1.
  Le poids des bras de la Rq issue du bras majeur de Rr est
  k2_1n2 = k1₁ – 2pq + p n2.
  Le poids des autres bras est
  k2_{n1 n2} = k1_n1 – pq + p n2.
  Le bras majeur est donc beau­coup plus gros que les autres.
• sur chaque bras libre de chaque Rq, une rosace Rp à p – 1 bras libres, à laquelle le bras de la Rq sert de B1. Le poids des bras de la Rp issue du bras majeur de la Rq est
  k3_n1.1n3 = k2_n1.1 – 2p + n3.
  Le poids des autres bras est
  k3_n1n2n3 = k2_n1n2 – p + n3.
  La rosace du bras majeur est donc plus grosse que les autres ;
• et bien enten­du tous les bras libres de ces Rp s’a­chèvent sur une ter­mi­nale récur­sive telle que
  k4_n1n2n3 = k3_n1n2n3 + n4.

L’ef­fet de ces for­mules est que le des­sin appa­raît à pre­mière vue comme une seule rosace Rp de poids k3_11n3, bien plus grosse que toutes les autres rosaces que l’ob­ser­va­tion atten­tive peut ensuite reconnaître.

Bien plus com­pli­quée que la struc­ture des des­sins de pre­mier niveau, celle des des­sins de niveaux supé­rieurs a été com­plè­te­ment éclair­cie, quel que soit le niveau, et résulte sim­ple­ment d’une appli­ca­tion sans conces­sion des lois pré­cé­dem­ment décou­vertes. Néan­moins, il n’est pas réa­liste de les pré­sen­ter ici.

Voir un exemple de rosace de 3^e niveau en figure 11.

Noyaux

La des­crip­tion pré­cé­dente, à base de bras de rosaces, ne concerne que les struc­tures majeures obte­nues en pla­çant bout à bout des car­dioïdes. On a bien fait état des rosaces laté­rales et de leur inter­pré­ta­tion, mais elles n’oc­cupent que peu de place dans les des­sins d’ensemble.

L’exa­men détaillé de ces struc­tures laté­rales per­met cepen­dant des décou­vertes remar­quables, en ce que leurs images com­binent les dis­po­si­tifs carac­té­ris­tiques du bras avec les consé­quences de la tra­ver­sée d’un cercle Cn subor­don­né à la micro­car­dioïde. L’ef­fet est de rem­pla­cer chaque micro­car­dioïde par une struc­ture com­plexe bap­ti­sée noyau.

Les lois de for­ma­tion des noyaux, qui com­binent plu­sieurs niveaux d’é­vo­ca­tion, ont été com­plè­te­ment déter­mi­nées. Il s’a­git d’i­mages excep­tion­nel­le­ment char­gées, et sou­vent fort belles, mais il est impos­sible de s’é­tendre sur ce vaste sujet dans l’es­pace dis­po­nible ici.

Le lec­teur doit cepen­dant être conscient que ces noyaux sont par­tout : en par­ti­cu­lier, tous les tri­plets de bras laté­raux sont des noyaux de C3.

Voir figure 12 pour un exemple.

---

Articles similaires :

Quelques sou­ve­nirs d’un petit colon fran­çais au Ton­kin (Viêt­nam)… La pro­duc­tion infor­ma­tique, élé­ment majeur du fonc­tion­ne­ment des entreprises Tho­mas Jef­fer­son et l’École poly­tech­nique : à la recherche des chaî­nons manquants Épi­dé­mio­lo­gie environnementale Alfred Gros­ser : réflexion sur le lien franco-allemand